
Automatic semigroup
Encyclopedia
In mathematics
, an automatic semigroup is a finitely generated semigroup
equipped with several regular languages over an alphabet representing a generating set. One of these languages determines "canonical forms" for the elements of the semigroup, the other languages determine if two canonical forms represent elements that differ by multiplication by a generator.
Formally, let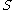 be a semigroup and
be a semigroup and 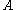 be a finite set of generators. Then an automatic structure for
be a finite set of generators. Then an automatic structure for 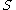 with respect to
with respect to 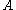 consists of a regular language
consists of a regular language 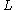 over
over 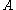 such that every element of
such that every element of  has at least one representative in
has at least one representative in 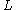 and such that for each
and such that for each 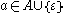 , the relation consisting of pairs
, the relation consisting of pairs 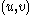 with
with 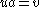 is regular.
is regular.
The concept of an automatic semigroup was generalized from automatic groups
by Campbell et al. (2001)
Unlike automatic groups (see Epstein et al. 1992), a semigroup may have an automatic structure with respect to one generating set, but not with respect to another. However, if an automatic semigroup has an identity, then it has an automatic structure with respect to any generating set (Duncan et al. 1999).
solvable in quadratic time. Kambites & Otto (2006) showed that it is undecidable whether an element of an automatic monoid possesses a right inverse.
Cain (2006) proved that both cancellativity and left-cancellativity are undecidable for automatic semigroups. On the other hand, right-cancellativity is decidable for automatic semigroups (Silva & Steinberg 2004).
-like' classes of semigroups, notably completely simple semigroups (Campbell et al. 2002) and group-embeddable semigroups (Cain et al. 2006).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an automatic semigroup is a finitely generated semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
equipped with several regular languages over an alphabet representing a generating set. One of these languages determines "canonical forms" for the elements of the semigroup, the other languages determine if two canonical forms represent elements that differ by multiplication by a generator.
Formally, let
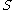 be a semigroup and
be a semigroup and 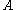 be a finite set of generators. Then an automatic structure for
be a finite set of generators. Then an automatic structure for 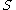 with respect to
with respect to 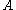 consists of a regular language
consists of a regular language 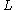 over
over 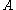 such that every element of
such that every element of  has at least one representative in
has at least one representative in 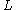 and such that for each
and such that for each 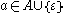 , the relation consisting of pairs
, the relation consisting of pairs 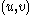 with
with 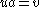 is regular.
is regular.The concept of an automatic semigroup was generalized from automatic groups
Automatic group
In mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.More...
by Campbell et al. (2001)
Unlike automatic groups (see Epstein et al. 1992), a semigroup may have an automatic structure with respect to one generating set, but not with respect to another. However, if an automatic semigroup has an identity, then it has an automatic structure with respect to any generating set (Duncan et al. 1999).
Decision problems
Like automatic groups, automatic semigroups have word problemWord problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
solvable in quadratic time. Kambites & Otto (2006) showed that it is undecidable whether an element of an automatic monoid possesses a right inverse.
Cain (2006) proved that both cancellativity and left-cancellativity are undecidable for automatic semigroups. On the other hand, right-cancellativity is decidable for automatic semigroups (Silva & Steinberg 2004).
Geometric characterization
Automatic structures for groups have an elegant geometric characterization called the fellow traveller property (Epstein et al. 1992, ch. 2). Automatic structures for semigroups possess the fellow traveller property but are not in general characterized by it (Campbell et al. 2001). However, the characterization can be generalized to certain 'groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
-like' classes of semigroups, notably completely simple semigroups (Campbell et al. 2002) and group-embeddable semigroups (Cain et al. 2006).
Examples of automatic semigroups
- Bicyclic monoid
- Finitely generated subsemigroups of a free semigroupFree semigroupIn abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...

