
Relatively hyperbolic group
Encyclopedia
In mathematics
, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory
concept of a hyperbolic group
. The motivating examples of relatively hyperbolic groups are the fundamental group
s of complete noncompact hyperbolic manifold
s of finite volume.
G is relatively hyperbolic with respect to a subgroup
H if, after contracting the Cayley graph
of G along H-coset
s, the resulting graph equipped with the usual graph metric becomes a δ-hyperbolic space and, moreover, it satisfies a technical condition which implies that quasi-geodesics with common endpoints travel through approximately the same collection of cosets and enter and exit these cosets in approximately the same place.
 as follows: For each left coset gH, add a vertex v(gH) to the Cayley graph Γ(G) and for each element x of gH, add an edge e(x) of length 1/2 from x to the vertex v(gH). This results in a metric space that may not be proper (i.e. closed balls need not be compact).
as follows: For each left coset gH, add a vertex v(gH) to the Cayley graph Γ(G) and for each element x of gH, add an edge e(x) of length 1/2 from x to the vertex v(gH). This results in a metric space that may not be proper (i.e. closed balls need not be compact).
The definition of a relatively hyperbolic group, as formulated by Bowditch
goes as follows. A group G is said to be hyperbolic relative to a subgroup H if the coned off Cayley graph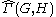 has the properties:
has the properties:
If only the first condition holds then the group G is said to be weakly relatively hyperbolic with respect to H.
The definition of the coned off Cayley graph can be generalized to the case of a collection of subgroups and yields the corresponding notion of relative hyperbolicity. A group G which contains no collection of subgroups with respect to which it is relatively hyperbolic is said to be a non relatively hyperbolic group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
concept of a hyperbolic group
Hyperbolic group
In group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
. The motivating examples of relatively hyperbolic groups are the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s of complete noncompact hyperbolic manifold
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
s of finite volume.
Intuitive definition
A groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is relatively hyperbolic with respect to a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
H if, after contracting the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of G along H-coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s, the resulting graph equipped with the usual graph metric becomes a δ-hyperbolic space and, moreover, it satisfies a technical condition which implies that quasi-geodesics with common endpoints travel through approximately the same collection of cosets and enter and exit these cosets in approximately the same place.
Formal definition
Given a finitely generated group G with Cayley graph Γ(G) equipped with the path metric and a subgroup H of G, one can construct the coned off Cayley graph as follows: For each left coset gH, add a vertex v(gH) to the Cayley graph Γ(G) and for each element x of gH, add an edge e(x) of length 1/2 from x to the vertex v(gH). This results in a metric space that may not be proper (i.e. closed balls need not be compact).
as follows: For each left coset gH, add a vertex v(gH) to the Cayley graph Γ(G) and for each element x of gH, add an edge e(x) of length 1/2 from x to the vertex v(gH). This results in a metric space that may not be proper (i.e. closed balls need not be compact).The definition of a relatively hyperbolic group, as formulated by Bowditch
Brian Bowditch
Brian Hayward Bowditch is a British mathematician known for his contributions to geometry and topology, particularly in the areas of geometric group theory and low-dimensional topology. He is also known for solving the angel problem...
goes as follows. A group G is said to be hyperbolic relative to a subgroup H if the coned off Cayley graph
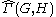 has the properties:
has the properties:
- It is δ-hyperbolic and
- it is fine: for each integer L, every edge belongs to only finitely many simple cycles of length L.
If only the first condition holds then the group G is said to be weakly relatively hyperbolic with respect to H.
The definition of the coned off Cayley graph can be generalized to the case of a collection of subgroups and yields the corresponding notion of relative hyperbolicity. A group G which contains no collection of subgroups with respect to which it is relatively hyperbolic is said to be a non relatively hyperbolic group.
Properties
- If a group G is relatively hyperbolic with respect to a hyperbolic group H, then G itself is hyperbolic.
Examples
- Any hyperbolic groupHyperbolic groupIn group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
, such as a free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of finite rank or the fundamental group of a hyperbolic surface, is hyperbolic relative to the trivial subgroup.
- The fundamental group of a complete hyperbolic manifoldHyperbolic manifoldIn mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
of finite volume is hyperbolic relative to its cusp subgroup. A similar result holds for any complete finite volume Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with pinched negative sectional curvatureSectional curvatureIn Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
.
- The free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
Z2 of rank 2 is weakly hyperbolic, but not hyperbolic, relative to the cyclic subgroup Z: even though the graph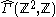 is hyperbolic, it is not fine.
is hyperbolic, it is not fine.
- The mapping class groupMapping class groupIn mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
of an orientable finite type surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
is either hyperbolic (when 3g+n<5, where g is the genus and n is the number of punctures) or is not relatively hyperbolic.
- The automorphism group and the outer automorphism group of a free group of finite rank at least 3 are not relatively hyperbolic.

