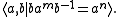Baumslag–Solitar group
Encyclopedia
In the mathematical
field of group theory
, the Baumslag–Solitar groups are examples of two-generator one-relator groups that play an important role in combinatorial group theory
and geometric group theory
as (counter)examples and test-cases. They are given by the group presentation
For each integer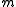
and 
, the Baumslag–Solitar group is denoted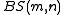 
. The relation in the presentation is called the Baumslag–Solitar relation.
Some of the various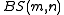
are well-known groups. 
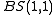is the free abelian group
on two generators
, and
is the Klein bottle
group.
The groups were defined by Gilbert Baumslag
and Donald Solitar in 1962 to provide examples of non-Hopfian
groups. The groups contain residually finite groups, Hopfian groups that are not residually finite, and non-Hopfian groups.
and 
. The matrix group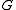 
generated by 
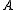and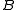 
is a homomorphic image of 
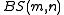, via the homomorphism 
, 
.
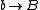It is worth noting that this will not, in general, be an isomorphism. For instance if
is not residually finite (ie, if it is not the case that 
, 
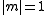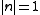, or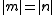 
) it cannot be isomorphic to a finitely generated linear group, which is known to be residually finite by a theorem of Mal'cev.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Baumslag–Solitar groups are examples of two-generator one-relator groups that play an important role in combinatorial group theory
Combinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
and geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
as (counter)examples and test-cases. They are given by the group presentation
For each integer
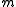and , the Baumslag–Solitar group is denoted 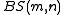. The relation in the presentation is called the Baumslag–Solitar relation.Some of the various
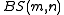are well-known groups. 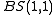is the free abelian groupFree abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
on two generators
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
, and
is the Klein bottleKlein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
group.
The groups were defined by Gilbert Baumslag
Gilbert Baumslag
Gilbert Baumslag is a Distinguished Professor at the City College of New York, with joint appointments in mathematics, computer science, and electrical engineering. He is director of the Center for Algorithms and Interactive Scientific Software, which grew out of the MAGNUS computational group...
and Donald Solitar in 1962 to provide examples of non-Hopfian
Hopfian group
In mathematics, a Hopfian group is a group G for which every epimorphismis an isomorphism. Equivalently, a group is Hopfian if and only if it is not isomorphic to any of its proper quotients. A group G is co-Hopfian if everymonomorphism...
groups. The groups contain residually finite groups, Hopfian groups that are not residually finite, and non-Hopfian groups.
Linear representation
Define and . The matrix group 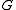generated by 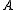and 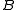is a homomorphic image of 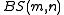, via the homomorphism , 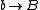.It is worth noting that this will not, in general, be an isomorphism. For instance if
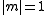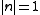is not residually finite (ie, if it is not the case that , , or 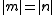) it cannot be isomorphic to a finitely generated linear group, which is known to be residually finite by a theorem of Mal'cev.