Complete set of invariants
Encyclopedia
In mathematics
, a complete set of invariant
s for a classification problem is a collection of maps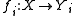
(where X is the collection of objects being classified, up to some equivalence relation, and the are some sets), such that
are some sets), such that  ∼
∼ 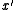 if and only if
if and only if 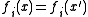 for all i. In words, such that two objects are equivalent if and only if all invariants are equal.
for all i. In words, such that two objects are equivalent if and only if all invariants are equal.
Symbolically, a complete set of invariants is a collection of maps such that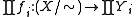
is injective.
As invariants are, by definition, equal on equivalent objects, equality of invariants is a necessary condition for equivalence; a complete set of invariants is a set such that equality of these is sufficient for equivalence. In the context of a group action, this may be stated as: invariants are functions of coinvariants (equivalence classes, orbits), and a complete set of invariants characterizes the coinvariants (is a set of defining equations for the coinvariants).
: not all combinations of invariants may be realized. Symbolically, one must also determine the image of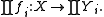
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a complete set of invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
s for a classification problem is a collection of maps
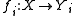
(where X is the collection of objects being classified, up to some equivalence relation, and the
 are some sets), such that
are some sets), such that  ∼
∼ 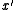 if and only if
if and only if 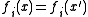 for all i. In words, such that two objects are equivalent if and only if all invariants are equal.
for all i. In words, such that two objects are equivalent if and only if all invariants are equal.Symbolically, a complete set of invariants is a collection of maps such that
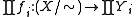
is injective.
As invariants are, by definition, equal on equivalent objects, equality of invariants is a necessary condition for equivalence; a complete set of invariants is a set such that equality of these is sufficient for equivalence. In the context of a group action, this may be stated as: invariants are functions of coinvariants (equivalence classes, orbits), and a complete set of invariants characterizes the coinvariants (is a set of defining equations for the coinvariants).
Examples
- In the classification of two-dimensional closed manifolds, Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
(or genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
) and orientabilityOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
are a complete set of invariants. - Jordan normal formJordan normal formIn linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
of a matrix is a complete invariant for matrices up to conjugation, but eigenvalues (with multiplicities) are not.
Realizability of invariants
A complete set of invariants does not immediately yield a classification theoremClassification theorem
In mathematics, a classification theorem answers the classification problem "What are the objects of a given type, up to some equivalence?". It gives a non-redundant enumeration: each object is equivalent to exactly one class....
: not all combinations of invariants may be realized. Symbolically, one must also determine the image of