Assembly map
Encyclopedia
In mathematics
, assembly maps are an important concept in geometric topology
. From the homotopy
-theoretical viewpoint, an assembly map is a universal
approximation of a homotopy invariant functor
by a homology theory
from the left. From the geometric viewpoint, assembly maps correspond to 'assemble' local data over a parameter space together to get global data.
Assembly maps for algebraic K-theory
and L-theory
play a central role in the topology of high-dimensional manifold
s, since their homotopy fiber
s have a direct geometric interpretation. Equivariant assembly maps are used to formulate the Farrell–Jones conjecture
s in K- and L-theory.
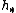on the category of topological spaces
(assumed to be homotopy equivalent to CW-complexes), there is a spectrum
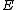such that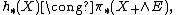
where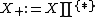
.
The functor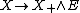
from spaces to spectra has the following properties:
A functor from spaces to spectra fulfilling these properties is called excisive.
Now suppose that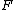
is a homotopy-invariant, not necessarily excisive functor. An assembly map is a natural transformation
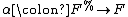from some excisive functor 
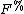to 
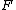such that 
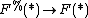is a homotopy equivalence.
If we denote by
the associated homology theory, it follows that the induced natural transformation of graded abelian group
s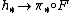
is the universal transformation from a homology theory to 
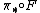, i.e. any other transformation 
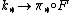from some homology theory 
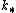factors uniquely through a transformation of homology theories 
.
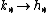Assembly maps exist for any homotopy invariant functor, by a simple homotopy-theoretical construction.
, the value of an excisive functor on a space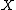
only depends on its value on 'small' subspaces of 
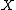, together with the knowledge how these small subspaces intersect. In a cycle representation of the associated homology theory, this means that all cycles must be representable by small cycles. For instance, for singular homology
, the excision property is proved by subdivision of simplices
, obtaining sums of small simplices representing arbitrary homology classes.
In this spirit, for certain homotopy-invariant functors which are not excisive, the corresponding excisive theory may be constructed by imposing 'control conditions', leading to the field of controlled topology. In this picture, assembly maps are 'forget-control' maps, i.e. they are induced by forgetting the control conditions.
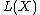, algebraic L-theory
of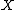
, and 
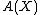, algebraic K-theory
of spaces of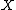
. In fact, the homotopy fibers of both assembly maps have a direct geometric interpretation when 
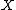is a compact topological manifold. Therefore knowledge about the geometry of compact topological manifolds may be obtained by studying 
- and 
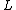-theory and their respective assembly maps.
In the case of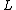
-theory, the homotopy fiber 
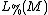of the corresponding assembly map 
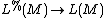, evaluated at a compact topological manifold 
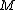, is homotopy equivalent to the space of block structures of 
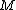. Moreover, the fibration sequence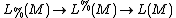
induces a long exact sequence of homotopy groups which may be identified with the surgery exact sequence of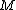
. This may be called the fundamental theorem of surgery theory and was developed subsequently by Browder, Novikov, Sullivan, Wall, Quinn, and Ranicki.
For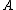
-theory, the homotopy fiber 
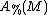of the corresponding assembly map is homotopy equivalent to the space of stable h-cobordism
s on
. This fact is called the stable parametrized h-cobordism theorem, proven by Waldhausen-Jahren-Rognes. It may be viewed as a parametrized version of the classical theorem which states that equivalence classes of h-cobordisms on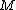 
are in 1-to-1 correspondence with elements in the Whitehead group
of
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, assembly maps are an important concept in geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
. From the homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
-theoretical viewpoint, an assembly map is a universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
approximation of a homotopy invariant functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
by a homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
from the left. From the geometric viewpoint, assembly maps correspond to 'assemble' local data over a parameter space together to get global data.
Assembly maps for algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
and L-theory
L-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
play a central role in the topology of high-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, since their homotopy fiber
Homotopy fiber
In mathematics, especially homotopy theory, the homotopy fiber is part of a construction that associates a fibration to an arbitrary continuous function of topological spaces f \colon A \to B....
s have a direct geometric interpretation. Equivariant assembly maps are used to formulate the Farrell–Jones conjecture
Farrell–Jones conjecture
In mathematics, the Farrell–Jones conjecture, named after F. Thomas Farrell and Lowell Edwin Jones states that certain assembly maps are isomorphisms...
s in K- and L-theory.
Homotopy-theoretical viewpoint
It is a classical result that for any generalized homology theoryHomology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
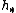on the category of topological spacesCategory of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
(assumed to be homotopy equivalent to CW-complexes), there is a spectrum
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
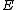such that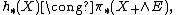where
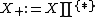.The functor
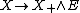from spaces to spectra has the following properties:
- It is homotopy-invariant (preserves homotopy equivalences). This reflects the fact that
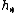is homotopy-invariant. - It preserves homotopy co-cartesian squares. This reflects that fact that
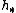has Mayer-Vietoris sequenceMayer-Vietoris sequenceIn mathematics, particularly algebraic topology and homology theory, the Mayer–Vietoris sequence is an algebraic tool to help compute algebraic invariants of topological spaces, known as their homology and cohomology groups. The result is due to two Austrian mathematicians, Walther Mayer and...
s, an equivalent characterization of excision. - It preserves arbitrary coproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s. This reflects the disjoint-union axiom of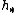
.
A functor from spaces to spectra fulfilling these properties is called excisive.
Now suppose that
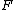is a homotopy-invariant, not necessarily excisive functor. An assembly map is a natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
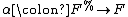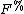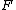from some excisive functor to such that 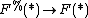is a homotopy equivalence.If we denote by
the associated homology theory, it follows that the induced natural transformation of graded abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s
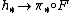is the universal transformation from a homology theory to 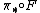, i.e. any other transformation 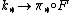from some homology theory 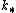factors uniquely through a transformation of homology theories 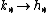.Assembly maps exist for any homotopy invariant functor, by a simple homotopy-theoretical construction.
Geometric viewpoint
As a consequence of the Mayer-Vietoris sequenceMayer-Vietoris sequence
In mathematics, particularly algebraic topology and homology theory, the Mayer–Vietoris sequence is an algebraic tool to help compute algebraic invariants of topological spaces, known as their homology and cohomology groups. The result is due to two Austrian mathematicians, Walther Mayer and...
, the value of an excisive functor on a space
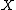only depends on its value on 'small' subspaces of 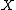, together with the knowledge how these small subspaces intersect. In a cycle representation of the associated homology theory, this means that all cycles must be representable by small cycles. For instance, for singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
, the excision property is proved by subdivision of simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, obtaining sums of small simplices representing arbitrary homology classes.
In this spirit, for certain homotopy-invariant functors which are not excisive, the corresponding excisive theory may be constructed by imposing 'control conditions', leading to the field of controlled topology. In this picture, assembly maps are 'forget-control' maps, i.e. they are induced by forgetting the control conditions.
Importance in geometric topology
Assembly maps are studied in geometric topology mainly for the two functors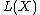, algebraic L-theoryL-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
of
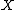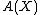, and , algebraic K-theoryAlgebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
of spaces of
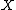. In fact, the homotopy fibers of both assembly maps have a direct geometric interpretation when 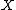is a compact topological manifold. Therefore knowledge about the geometry of compact topological manifolds may be obtained by studying - and 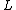-theory and their respective assembly maps.In the case of
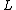-theory, the homotopy fiber 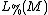of the corresponding assembly map 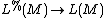, evaluated at a compact topological manifold 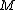, is homotopy equivalent to the space of block structures of 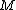. Moreover, the fibration sequence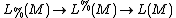induces a long exact sequence of homotopy groups which may be identified with the surgery exact sequence of
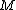. This may be called the fundamental theorem of surgery theory and was developed subsequently by Browder, Novikov, Sullivan, Wall, Quinn, and Ranicki.For
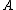-theory, the homotopy fiber 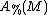of the corresponding assembly map is homotopy equivalent to the space of stable h-cobordismH-cobordism
A cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
s on
. This fact is called the stable parametrized h-cobordism theorem, proven by Waldhausen-Jahren-Rognes. It may be viewed as a parametrized version of the classical theorem which states that equivalence classes of h-cobordisms on 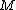are in 1-to-1 correspondence with elements in the Whitehead groupWhitehead group
Whitehead group in mathematics may mean:* A group W with Ext=0; see Whitehead problem* For a ring, the Whitehead group Wh of a ring A, equal to K_1...
of
.