
Homotopy fiber
Encyclopedia
In mathematics
, especially homotopy theory, the homotopy fiber is part of a construction that associates a fibration
to an arbitrary continuous function
of topological spaces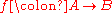 .
.
In particular, given such a map, define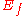 to be the set of pairs
to be the set of pairs  where
where 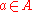 and
and  is a path such that
is a path such that 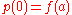 . We give
. We give  a topology by giving it the subspace topology as a subset of
a topology by giving it the subspace topology as a subset of 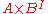 (where
(where  is the space of paths in
is the space of paths in  which as a function space
which as a function space
has the compact-open topology
). Then the map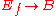 given by
given by  is a fibration. Furthermore,
is a fibration. Furthermore, 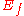 is homotopy equivalent to
is homotopy equivalent to  as follows: Embed
as follows: Embed  as a subspace of
as a subspace of  by
by 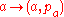 where
where 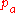 is the constant path at
is the constant path at 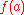 . Then
. Then  deformation retract
deformation retract
s to this subspace by contracting the paths.
The fiber of this fibration (which is only well-defined up to homotopy equivalence) is the homotopy fiber , which can be defined as the set of all
, which can be defined as the set of all 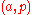 with
with 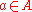 and
and  a path such that
a path such that 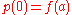 and
and 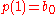 , where
, where 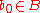 is some fixed basepoint of
is some fixed basepoint of  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially homotopy theory, the homotopy fiber is part of a construction that associates a fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
to an arbitrary continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of topological spaces
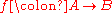 .
.In particular, given such a map, define
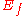 to be the set of pairs
to be the set of pairs  where
where 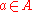 and
and  is a path such that
is a path such that 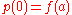 . We give
. We give  a topology by giving it the subspace topology as a subset of
a topology by giving it the subspace topology as a subset of 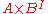 (where
(where  is the space of paths in
is the space of paths in  which as a function space
which as a function spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
has the compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
). Then the map
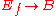 given by
given by  is a fibration. Furthermore,
is a fibration. Furthermore, 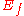 is homotopy equivalent to
is homotopy equivalent to  as follows: Embed
as follows: Embed  as a subspace of
as a subspace of  by
by 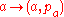 where
where 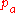 is the constant path at
is the constant path at 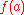 . Then
. Then  deformation retract
deformation retractDeformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
s to this subspace by contracting the paths.
The fiber of this fibration (which is only well-defined up to homotopy equivalence) is the homotopy fiber
 , which can be defined as the set of all
, which can be defined as the set of all 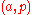 with
with 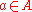 and
and  a path such that
a path such that 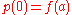 and
and 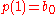 , where
, where 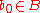 is some fixed basepoint of
is some fixed basepoint of  .
.

