Normal bundle
Encyclopedia
In differential geometry, a field of mathematics
, a normal bundle is a particular kind of vector bundle
, complementary to the tangent bundle
, and coming from an embedding
(or immersion).
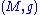be a Riemannian manifold
, and
a Riemannian submanifold
. Define, for a given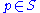
, a vector 
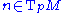to be normal to 
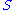whenever 
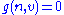for all 
(so that 
is orthogonal to 
). The set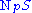 
of all such 
is then called the normal space to 
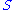at 
.
Just as the total space of the tangent bundle
to a manifold is constructed from all tangent space
s to the manifold, the total space of the normal bundle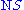
to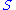 
is defined as
.
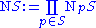The conormal bundle is defined as the dual bundle
to the normal bundle. It can be realised naturally as a sub-bundle of the cotangent bundle
.
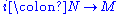(for instance an embedding), one can define a normal bundle of N in M, by at each point of N, taking the quotient space
of the tangent space on M by the tangent space on N. For a Riemannian manifold one can identify this quotient with the orthogonal complement, but in general one cannot (such a choice is equivalent to a section
of the projection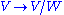
).
Thus the normal bundle is in general a quotient of the tangent bundle of the ambient space restricted to the subspace.
Formally, the normal bundle to N in M is a quotient bundle of the tangent bundle on M: one has the short exact sequence of vector bundles on N:
where
is the restriction of the tangent bundle on M to N (properly, the pullback 
of the tangent bundle on M to a vector bundle on N via the map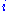 
).
manifolds have a canonical
tangent bundle, but do not have a normal bundle: only an embedding (or immersion) of a manifold in another yields a normal bundle.
However, since every compact manifold can be embedded in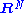
, by the Whitney embedding theorem, every manifold admits a normal bundle, given such an embedding.
There is in general no natural choice of embedding, but for a given M, any two embeddings in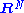
for sufficiently large N are regular homotopic
, and hence induce the same normal bundle. The resulting class of normal bundles (it is a class of bundles and not a specific bundle because N could vary) is called the stable normal bundle
.
:
by the above short exact sequence,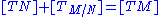
in the Grothendieck group
.
In case of an immersion in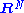
, the tangent bundle of the ambient space is trivial (since 
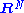is contractible, hence parallelizable), so 
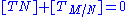, and thus 
.
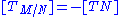This is useful in the computation of characteristic classes, and allows one to prove lower bounds on immersibility and embeddability of manifolds in Euclidean space
.
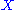is embedded in to a symplectic manifold
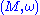, such that the pullback of the symplectic form has constant rank on 
. Then one can define the symplectic normal bundle to X as the vector bundle over X with fibres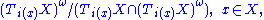
where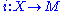
denotes the embedding. Notice that the constant rank condition ensures that these normal spaces fit together to form a bundle. Furthermore, any fibre inherits the structure of a symplectic vector space.
By Darboux's theorem
, the constant rank embedding is locally determined by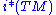
. The isomorphism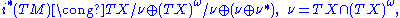
of symplectic vector bundles over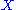
implies that the symplectic normal bundle already determines the constant rank embedding locally. This feature is similar to the Riemannian case.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a normal bundle is a particular kind of vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, complementary to the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, and coming from an embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
(or immersion).
Riemannian manifold
Let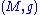 be a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, and
a Riemannian submanifoldRiemannian submanifold
A Riemannian submanifold N of a Riemannian manifold M is a submanifold of M equipped with the Riemannian metric inherited from M. The image of an isometric immersion is a Riemannian submanifold....
. Define, for a given
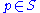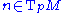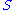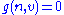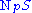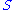, a vector to be normal to whenever for all (so that is orthogonal to ). The set of all such is then called the normal space to at .Just as the total space of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
to a manifold is constructed from all tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s to the manifold, the total space of the normal bundle
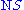to 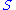is defined as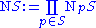.The conormal bundle is defined as the dual bundle
Dual bundle
In mathematics, the dual bundle of a vector bundle π : E → X is a vector bundle π* : E* → X whose fibers are the dual spaces to the fibers of E...
to the normal bundle. It can be realised naturally as a sub-bundle of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
.
General definition
More abstractly, given an immersion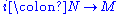 (for instance an embedding), one can define a normal bundle of N in M, by at each point of N, taking the quotient spaceQuotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
of the tangent space on M by the tangent space on N. For a Riemannian manifold one can identify this quotient with the orthogonal complement, but in general one cannot (such a choice is equivalent to a section
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of the projection
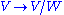).Thus the normal bundle is in general a quotient of the tangent bundle of the ambient space restricted to the subspace.
Formally, the normal bundle to N in M is a quotient bundle of the tangent bundle on M: one has the short exact sequence of vector bundles on N:
where
is the restriction of the tangent bundle on M to N (properly, the pullback of the tangent bundle on M to a vector bundle on N via the map 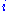).Stable normal bundle
AbstractAbstraction
Abstraction is a process by which higher concepts are derived from the usage and classification of literal concepts, first principles, or other methods....
manifolds have a canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
tangent bundle, but do not have a normal bundle: only an embedding (or immersion) of a manifold in another yields a normal bundle.
However, since every compact manifold can be embedded in
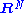, by the Whitney embedding theorem, every manifold admits a normal bundle, given such an embedding.There is in general no natural choice of embedding, but for a given M, any two embeddings in
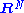for sufficiently large N are regular homotopicRegular homotopy
In the mathematical field of topology, a regular homotopy refers to a special kind of homotopy between immersions of one manifold in another. The homotopy must be a 1-parameter family of immersions....
, and hence induce the same normal bundle. The resulting class of normal bundles (it is a class of bundles and not a specific bundle because N could vary) is called the stable normal bundle
Stable normal bundle
In surgery theory, a branch of mathematics, the stable normal bundle of a differentiable manifold is an invariant which encodes the stable normal data. There are analogs for generalizations of manifold, notably PL-manifolds and topological manifolds...
.
Dual to tangent bundle
The normal bundle is dual to the tangent bundle in the sense of K-theoryK-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
:
by the above short exact sequence,
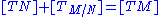
in the Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
.
In case of an immersion in
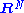, the tangent bundle of the ambient space is trivial (since 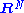is contractible, hence parallelizable), so 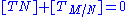, and thus 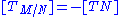.This is useful in the computation of characteristic classes, and allows one to prove lower bounds on immersibility and embeddability of manifolds in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
For symplectic manifolds
Suppose a manifold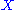 is embedded in to a symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
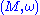, such that the pullback of the symplectic form has constant rank on . Then one can define the symplectic normal bundle to X as the vector bundle over X with fibres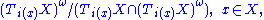where
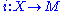denotes the embedding. Notice that the constant rank condition ensures that these normal spaces fit together to form a bundle. Furthermore, any fibre inherits the structure of a symplectic vector space.By Darboux's theorem
Darboux's theorem
Darboux's theorem is a theorem in the mathematical field of differential geometry and more specifically differential forms, partially generalizing the Frobenius integration theorem. It is a foundational result in several fields, the chief among them being symplectic geometry...
, the constant rank embedding is locally determined by
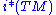. The isomorphism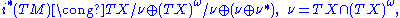of symplectic vector bundles over
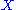implies that the symplectic normal bundle already determines the constant rank embedding locally. This feature is similar to the Riemannian case.