Section (category theory)
Encyclopedia
In category theory
, a branch of mathematics
, a section (or coretraction) is a right inverse of a morphism. Dually
, a retraction (or retract) is a left inverse. In other words, if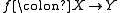
and 
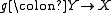are morphisms whose composition 
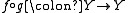is the identity morphism on 
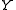, then 
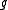is a section of 
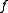, and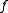 
is a retraction of 
.
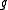If section of a morphism exists, it is called sectionable. Dually, if retraction of a morphism exists, it is called retractable.
The categorical concept of a section is important in homological algebra
, and is also closely related to the notion of a section of a fiber bundle
in topology: in the latter case, a section of a fiber bundle is a section of the bundle projection map of the fiber bundle
.
Every section is a monomorphism
, and every retraction is an epimorphism
;
they are called respectively a split monomorphism and a split epimorphism (the inverse is the splitting).
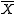with quotient map 
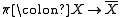, a section of 
is called a transversal
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a section (or coretraction) is a right inverse of a morphism. Dually
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
, a retraction (or retract) is a left inverse. In other words, if
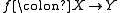and 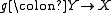are morphisms whose composition 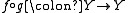is the identity morphism on 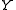, then 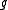is a section of 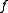, and 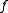is a retraction of 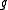.If section of a morphism exists, it is called sectionable. Dually, if retraction of a morphism exists, it is called retractable.
The categorical concept of a section is important in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, and is also closely related to the notion of a section of a fiber bundle
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
in topology: in the latter case, a section of a fiber bundle is a section of the bundle projection map of the fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
.
Every section is a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, and every retraction is an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
;
they are called respectively a split monomorphism and a split epimorphism (the inverse is the splitting).
Examples
Given a quotient spaceQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
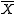with quotient map 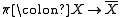, a section of is called a transversalTransversal
In geometry , when two coplanar lines exist such that a third coplanar line passes thru both lines. This third line is named the Transversal....
.