Regular homotopy
Encyclopedia
In the mathematical
field of topology
, a regular homotopy refers to a special kind of homotopy
between immersions of one manifold
in another. The homotopy must be a 1-parameter family of immersions.
Similar to homotopy classes, one defines two immersions to be in the same regular homotopy class if there exists a regular homotopy between them. Regular homotopy for immersions is similar to isotopy of embeddings: they are both restricted types of homotopies. Stated another way, two continuous functions
are homotopic if they represent points in the same path-components of the mapping space 
, given the compact-open topology
. The space of immersions is the subspace of
consisting of immersions, denote it by 
. Two immersions 
are regularly homotopic if they represent points in the same path-component of 
.
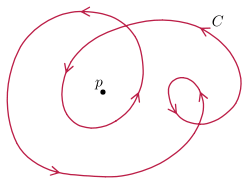The Whitney–Graustein theorem classifies the regular homotopy classes of a circle into the plane; two immersions are regularly homotopic if and only if they have the same turning number – equivalently, total curvature
; equivalently, if and only if their Gauss map
s have the same degree/winding number
.
Stephen Smale
classified the regular homotopy classes of a k-sphere immersed in
– they are classified by homotopy groups of Stiefel manifold
s, which is a generalization of the Gauss map, with here k partial derivatives not vanishing. A corollary of his work is that there is only one regular homotopy class of a 2-sphere immersed in
. In particular, this means that sphere eversions exist, i.e. one can turn the 2-sphere "inside-out".
Both of these examples consist of reducing regular homotopy to homotopy; this has subsequently been substantially generalized in the homotopy principle (or h-principle) approach.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a regular homotopy refers to a special kind of homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
between immersions of one manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
in another. The homotopy must be a 1-parameter family of immersions.
Similar to homotopy classes, one defines two immersions to be in the same regular homotopy class if there exists a regular homotopy between them. Regular homotopy for immersions is similar to isotopy of embeddings: they are both restricted types of homotopies. Stated another way, two continuous functions
are homotopic if they represent points in the same path-components of the mapping space , given the compact-open topologyCompact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
. The space of immersions is the subspace of
consisting of immersions, denote it by . Two immersions are regularly homotopic if they represent points in the same path-component of .Examples
Total curvature
In mathematical study of the differential geometry of curves, the total curvature of an immersed plane curve is the integral of curvature along a curve taken with respect to arclength:\int_a^b k\,ds....
; equivalently, if and only if their Gauss map
Gauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
s have the same degree/winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
.
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
classified the regular homotopy classes of a k-sphere immersed in
– they are classified by homotopy groups of Stiefel manifoldStiefel manifold
In mathematics, the Stiefel manifold Vk is the set of all orthonormal k-frames in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel...
s, which is a generalization of the Gauss map, with here k partial derivatives not vanishing. A corollary of his work is that there is only one regular homotopy class of a 2-sphere immersed in
. In particular, this means that sphere eversions exist, i.e. one can turn the 2-sphere "inside-out".Both of these examples consist of reducing regular homotopy to homotopy; this has subsequently been substantially generalized in the homotopy principle (or h-principle) approach.