Immersion (mathematics) - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, an immersion is a differentiable map between differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

s whose derivative is everywhere injective.
Explicitly, f : M → N is an immersion if

is an injective map at every point p of M (where the notation

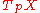represents the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

at the point

). Equivalently, f is an immersion if it has constant rank equal to the dimension of M:

The map f itself need not be injective, only its derivative.

A related concept is that of an embedding

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

. A smooth embedding is an injective immersion f : M → N which is also a topological embedding, so that M is diffeomorphic to its image in N. An immersion is precisely a local embedding – i.e. for any point

there is a neighbourhood,

, of x such that

is an embedding, and conversely a local embedding is an immersion.

If M is compact, an injective immersion is an embedding, but if M is not compact then injective immersions need not be embeddings; compare to continuous bijections versus homeomorphism

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

Regular homotopy

A regular homotopy
Regular homotopy
In the mathematical field of topology, a regular homotopy refers to a special kind of homotopy between immersions of one manifold in another. The homotopy must be a 1-parameter family of immersions....

between two immersions f and g from a manifold M to a manifold N is defined to be a
differentiable function H: M × [0,1] → N such for all

the function H_t: M → N defined by H_t(x) = H(x,t) for all

is an immersion, with H₀ = f, H₁ = g. A regular homotopy is thus a homotopy

Homotopy

In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...

through immersions.

Classification

Hassler Whitney

Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...

initiated the systematic study of immersions and regular homotopies in the 1940s, proving that for

every map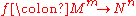

of an

-dimensional manifold to an

-dimensional manifold is homotopic to an immersion, and in fact to an embedding

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

for

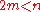; these are the Whitney immersion theorem and Whitney embedding theorem.

Stephen Smale expressed the regular homotopy classes of immersions

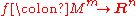as the homotopy groups of a certain Stiefel manifold

Stiefel manifold

In mathematics, the Stiefel manifold Vk is the set of all orthonormal k-frames in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel...

. The sphere eversion was a particularly striking consequence.

Morris Hirsch

Morris Hirsch

Morris William Hirsch is an American mathematician, formerly at the University of California, Berkeley.A native of Chicago, Illinois, Hirsch attained his doctorate from the University of Chicago in 1958, under supervision of Edwin Spanier and Stephen Smale. His thesis was entitled Immersions of...

generalized Smale's expression to a homotopy theory description of the regular homotopy classes of immersions of any m-dimensional manifold M^m in any n-dimensional manifold Nⁿ.

The Hirsch-Smale classification of immersions was generalized by Mikhail Gromov.

Existence

The primary obstruction to the existence of an immersion

is the stable normal bundle

Stable normal bundle

In surgery theory, a branch of mathematics, the stable normal bundle of a differentiable manifold is an invariant which encodes the stable normal data. There are analogs for generalizations of manifold, notably PL-manifolds and topological manifolds...

of M, as detected by its characteristic classes, notably its Stiefel–Whitney class

Stiefel–Whitney class

In mathematics, in particular in algebraic topology and differential geometry, the Stiefel–Whitney class is an example of a \mathbb Z_2characteristic class associated to real vector bundles.-General presentation:...

es. That is, since

is parallelizable, the pullback of its tangent bundle to M is trivial; since this pullback is the direct sum of the (intrinsically defined) tangent bundle on M, TM, which has dimension m, and of the normal bundle

of the immersion i, which has dimension

for there to be a codimension

Codimension

In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...

k immersion of M, there must be a vector bundle of dimension k,

standing in for the normal bundle

such that

is trivial. Conversely, given such a bundle, an immersion of M with this normal bundle is equivalent to a codimension 0 immersion of the total space of this bundle, which is an open manifold.

The stable normal bundle is the class of normal bundles plus trivial bundles, and thus if the stable normal bundle has cohomological dimension k, it cannot come from an (unstable) normal bundle of dimension less than k. Thus, the cohomology dimension of the stable normal bundle, as detected by its highest non-vanishing characteristic class, is an obstruction to immersions.

Since characteristic classes multiply under direct sum of vector bundles, this obstruction can be stated intrinsically in terms of the space M and its tangent bundle and cohomology algebra. This obstruction was stated (in terms of the tangent bundle, not stable normal bundle) by Whitney.

For example, the Möbius strip

Möbius strip

The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...

has non-trivial tangent bundle, so it cannot immerse in codimension 0 (in

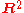), though it embeds in codimension 1 (in

).

In 1960, William S. Massey

William S. Massey

William Schumacher Massey is an American mathematician, known for his work in algebraic topology. The Massey product is named for him. He worked also on the formulation of spectral sequences by means of exact couples, and wrote several textbooks, including Algebraic Topology .William Massey was...

showed that these characteristic classes (the Stiefel–Whitney classes of the stable normal bundle) vanish above degree

where

is the number of “1” digits when n is written in binary; this bound is sharp, as realized by real projective space

Real projective space

In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...

. This gave evidence to the Immersion Conjecture, namely that every n-manifold could be immersed in codimension

i.e., in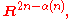

and was proven in 1985 by Ralph Cohen .

Codimension 0

Codimension 0 immersions are equivalently relative dimension

Relative dimension

In mathematics, specifically linear algebra and geometry, relative dimension is the dual notion to codimension.In linear algebra, given a quotient map V \to Q, the difference dim V − dim Q is the relative dimension; this equals the dimension of the kernel.In fiber bundles, the relative dimension of...

0 submersions
Submersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...

, and are better thought of as submersions.
A codimension 0 immersion of a closed manifold

Closed manifold

In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....

is precisely a covering map

Covering map

In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...

, i.e., a fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

with 0-dimensional (discrete) fiber. By Ehresmann's theorem

Ehresmann's theorem

In mathematics, Ehresmann's fibration theorem states that a smooth mappingwhere M and N are smooth manifolds, such that#f is a surjective submersion, and#f is a proper map,...

and Phillip's theorem on submersions, a proper

Proper map

In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...

submersion of manifolds is a fiber bundle, hence codimension/relative dimension 0 immersions/submersions behave like submersions.

Further, codimenson 0 immersions do not behave like other immersions, which are largely determined by the stable normal bundle: in codimension 0 one has issues of fundamental class

Fundamental class

In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...

and cover spaces. For instance, there is no codimension 0 immersion

despite the circle being parallelizable, which can be proven because the line has no fundamental class, so one does not get the required map on top cohomology. Alternatively, this is by invariance of domain

Invariance of domain

Invariance of domain is a theorem in topology about homeomorphic subsets of Euclidean space Rn. It states:The theorem and its proof are due to L.E.J. Brouwer, published in 1912...

. Similarly, although

and the 3-torus

are both parallelizable, there is no immersion

– any such cover would have to be ramified at some points, since the sphere is simply connected.

Another way of understanding this is that a codimension k immersion of a manifold corresponds to a codimension 0 immersion of a k-dimensional vector bundle, which is an open manifold if the codimension is greater than 0, but to a closed manifold in codimension 0 (if the original manifold is closed).

Multiple points

A -tuple point of an immersion f : M → N is an unordered set

of distinct points

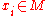with the same image

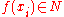. If M is an

-dimensional manifold and N is an

-dimensional manifold then for an immersion f : M → N in general position

General position

In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...

the set of

-tuple points is an

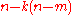-dimensional manifold.

A double point is a

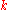-tuple point with

. An embedding is an immersion without double (or higher multiplicity) points, i.e. an embedding is an injective immersion.

The nature of the multiple points classifies immersions; for example, immersions of a circle in the plane are classified up to regular homotopy by the number of double points.

At a key point in surgery theory

Surgery theory

In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...

it is necessary to decide if an immersion

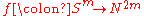of an

-sphere in a

-dimensional manifold is regular homotopic to an embedding, in which case it can be killed by surgery.
Wall associated to f an invariant

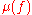in a quotient of the fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

ring

which counts the double points of f in the universal cover of

. For

is regular homotopic to an embedding if and only if

by the Whitney

Hassler Whitney

Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...

trick.

One can study embeddings as "immersions without multiple points", since immersions are easier to classify. Thus, one can start from immersions and try to eliminate multiple points, seeing if one can do this without introducing other singularities – studying "multiple disjunctions". This was first done by André Haefliger

André Haefliger

André Haefliger is a Swiss mathematician who works primarily on topology.He studied mathematics in Lausanne. He received his PhD in 1958 from the University of Strasbourg under the supervision of Charles Ehresmann with "Structures feuilletées et cohomologie à valeurs dans un faisceau de...

, and this approach is fruitful in codimension 3 or more – from the point of view of surgery theory, this is "high (co)dimension", unlike codimension 2 which is the knotting dimension, as in knot theory

Knot theory

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

. It is studied categorically via the "calculus of functors

Calculus of functors

In algebraic topology, a branch of mathematics, the calculus of functors or Goodwillie calculus is a technique for studying functors by approximating them by a sequence of simpler functors; it generalizes the sheafification of a presheaf...

" by Thomas Goodwillie, John Klein, and Michael S. Weiss.

Examples and properties

The Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...

, and all other non-orientable closed surfaces, can be immersed in 3-space but not embedded.

A mathematical rose
Rose (mathematics)
In mathematics, a rose or rhodonea curve is a sinusoid plotted in polar coordinates. Up to similarity, thesecurves can all be expressed by a polar equation of the form\!\,r=\cos.If k is an integer, the curve will be rose shaped with...

with petals is an immersion of the circle in the plane with a single -tuple point; k can be any odd number, but if even must be a multiple of 4, so the figure 8 is not a rose.
By the Whitney–Graustein theorem the regular homotopy classes of immersions of the circle in the plane are classified by the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...

which is also the number of double points counted algebraically (i.e. with signs).
The sphere can be turned inside out: the standard embedding 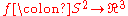is related to by a regular homotopy of immersions .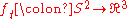
Boy's surface
Boy's surface
In geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901...

is an immersion of the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...

in 3-space; thus also a 2-to-1 immersion of the sphere.
The Morin surface
Morin surface
The Morin surface is the half-way model of the sphere eversion discovered by Bernard Morin. It features fourfold rotational symmetry.If the original sphere to be everted has its outer surface colored green and its inner surface colored red, then when the sphere is transformed through homotopy into...

is an immersion of the sphere; both it and Boy's surface arise as midway models in sphere eversion.

Immersed plane curves

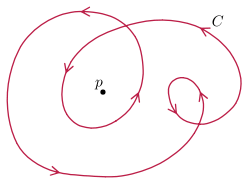
Immersed plane curves have a well-defined turning number, which can be defined as the total curvature

Total curvature

In mathematical study of the differential geometry of curves, the total curvature of an immersed plane curve is the integral of curvature along a curve taken with respect to arclength:\int_a^b k\,ds....

divided by 2π. This is invariant under regular homotopy, by the Whitney–Graustein theorem – topologically, it is the degree of the Gauss map

Gauss map

In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...

, or equivalently the winding number

Winding number

In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...

of the unit tangent (which does not vanish) about the origin. Further, this is the only invariant – any two plane curves with the same turning number are regular homotopic.

Every immersed plane curve lifts to an embedded space curve via separating the intersection points, which is not true in higher dimensions. With added data (which strand is on top), immersed plane curves yield knot diagrams, which are of central interest in knot theory

Knot theory

. While immersed plane curves, up to regular homotopy, are determined by their turning number, knots have a very rich and complex structure.

Immersed surfaces in 3-space

The study of immersed surfaces in 3-space is closely connected with the study of knotted (embedded) surfaces in 4-space, by analogy with the theory of knot diagrams (immersed plane curves (2-space) as projections of knotted curves in 3-space): given a knotted surface in 4-space, one can project it to an immersed surface in 3-space, and conversely, given an immersed surface in 3-space, one may ask if it lifts to 4-space – is it the projection of a knotted surface in 4-space? This allows one to relate questions about these objects.

A basic result, in contrast to the case of plane curves, is that not every immersed surface lifts to a knotted surface. In some cases the obstruction is 2-torsion, such as in Koschorke's example, which is an immersed surface (formed from 3 Möbius bands, with a triple point

Triple point

In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium...

) that does not lift to a knotted surface, but it has a double cover that does lift. A detailed analysis is given in , while a more recent survey is given in .

Generalizations

A far-reaching generalization of immersion theory is the homotopy principle:
one may consider the immersion condition (the rank of the derivative is always k) as a partial differential relation (PDR), as it can be stated in terms of the partial derivatives of the function. Then Smale–Hirsch immersion theory is the result that this reduces to homotopy theory, and the homotopy principle gives general conditions and reasons for PDRs to reduce to homotopy theory.