Relative dimension
Encyclopedia
In mathematics
, specifically linear algebra
and geometry
, relative dimension is the dual notion to codimension
.
In linear algebra, given a quotient map
, the difference dim V − dim Q is the relative dimension; this equals the dimension of the kernel.
In fiber bundle
s, the relative dimension of the map is the dimension of the fiber.
More abstractly, the codimension of a map is the dimension of the cokernel
, while the relative dimension of a map is the dimension of the kernel
.
These are dual in that the inclusion of a subspace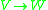
of codimension k dualizes to yield a quotient map 
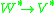of relative dimension k, and conversely.
The additivity of codimension under intersection corresponds to the additivity of relative dimension in a fiber product.
Just as codimension is mostly used for injective maps, relative dimension is mostly used for surjective maps.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, relative dimension is the dual notion to codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
.
In linear algebra, given a quotient map
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
, the difference dim V − dim Q is the relative dimension; this equals the dimension of the kernel.In fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s, the relative dimension of the map is the dimension of the fiber.
More abstractly, the codimension of a map is the dimension of the cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
, while the relative dimension of a map is the dimension of the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
.
These are dual in that the inclusion of a subspace
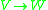of codimension k dualizes to yield a quotient map 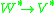of relative dimension k, and conversely.The additivity of codimension under intersection corresponds to the additivity of relative dimension in a fiber product.
Just as codimension is mostly used for injective maps, relative dimension is mostly used for surjective maps.