
Rank (differential topology)
Encyclopedia
In mathematics
, the rank of a differentiable map f : M → N between differentiable manifold
s at a point p ∈ M is the rank
of the derivative of f at p. Recall that the derivative of f at p is a linear map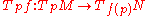
from the tangent space
at p to the tangent space at f(p). As a linear map between vector space
s it has a well-defined rank, which is just the dimension
of the image
in Tf(p)N:
.
Three special cases of constant rank maps occur. A constant rank map f : M → N is
The map f itself need not be injective, surjective, or bijective for these conditions to hold, only the behavior of the derivative is important. For example, there are injective maps which are not immersions and immersions which are not injections. However, if f : M → N is a smooth map of constant rank then
Constant rank maps have a nice description in terms of local coordinates
. Suppose M and N are smooth manifolds of dimensions m and n respectively, and f : M → N is a smooth map with constant rank k. Then for all p in M there exist coordinates (x1, ..., xm) centered at p and coordinates (y1, ..., yn) centered at f(p) such that f is given by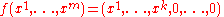
in these coordinates.
 Maps whose rank is generically maximal, but drops at certain singular points, occur frequently in coordinate system
Maps whose rank is generically maximal, but drops at certain singular points, occur frequently in coordinate system
s. For example, in spherical coordinates, the rank of the map from the two angles to a point on the sphere (formally, a map T2 → S2 from the torus
to the sphere) is 2 at regular points, but is only 1 at the north and south poles (zenith
and nadir
).
A subtler example occurs in charts on SO(3)
, the rotation group
. This group occurs widely in engineering, due to 3-dimensional rotations being heavily used in navigation
, nautical engineering, and aerospace engineering
, among many other uses. Topologically, SO(3) is the real projective space
RP3, and it is often desirable to represent rotations by a set of three numbers, known as Euler angles
(in numerous variants), both because this is conceptually simple, and because one can build a combination of three gimbal
s to produce rotations in three dimensions. Topologically this corresponds to a map from the 3-torus T3 of three angles to the real projective space RP3 of rotations, but this map does not have rank 3 at all points (formally because it cannot be a covering map
, as the only (non-trivial) covering space is the hypersphere S3), and the phenomenon of the rank dropping to 2 at certain points is referred to in engineering as gimbal lock
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the rank of a differentiable map f : M → N between differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s at a point p ∈ M is the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of the derivative of f at p. Recall that the derivative of f at p is a linear map
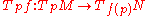
from the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at p to the tangent space at f(p). As a linear map between vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s it has a well-defined rank, which is just the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
in Tf(p)N:

Constant rank maps
A differentiable map f : M → N is said to have constant rank if the rank of f is the same for all p in M. Constant rank maps have a number of nice properties and are an important concept in differential topologyDifferential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
.
Three special cases of constant rank maps occur. A constant rank map f : M → N is
- an immersion if rank f = dim M (i.e. the derivative is everywhere injective),
- a submersionSubmersion (mathematics)In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
if rank f = dim N (i.e. the derivative is everywhere surjective), - a local diffeomorphismLocal diffeomorphismIn mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
if rank f = dim M = dim N (i.e. the derivative is everywhere bijective).
The map f itself need not be injective, surjective, or bijective for these conditions to hold, only the behavior of the derivative is important. For example, there are injective maps which are not immersions and immersions which are not injections. However, if f : M → N is a smooth map of constant rank then
- if f is injective it is an immersion,
- if f is surjective it is a submersion,
- if f is bijective it is a diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
.
Constant rank maps have a nice description in terms of local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
. Suppose M and N are smooth manifolds of dimensions m and n respectively, and f : M → N is a smooth map with constant rank k. Then for all p in M there exist coordinates (x1, ..., xm) centered at p and coordinates (y1, ..., yn) centered at f(p) such that f is given by
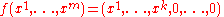
in these coordinates.
Examples

Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
s. For example, in spherical coordinates, the rank of the map from the two angles to a point on the sphere (formally, a map T2 → S2 from the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
to the sphere) is 2 at regular points, but is only 1 at the north and south poles (zenith
Zenith
The zenith is an imaginary point directly "above" a particular location, on the imaginary celestial sphere. "Above" means in the vertical direction opposite to the apparent gravitational force at that location. The opposite direction, i.e...
and nadir
Nadir
The nadir is the direction pointing directly below a particular location; that is, it is one of two vertical directions at a specified location, orthogonal to a horizontal flat surface there. Since the concept of being below is itself somewhat vague, scientists define the nadir in more rigorous...
).
A subtler example occurs in charts on SO(3)
Charts on SO(3)
In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...
, the rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
. This group occurs widely in engineering, due to 3-dimensional rotations being heavily used in navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
, nautical engineering, and aerospace engineering
Aerospace engineering
Aerospace engineering is the primary branch of engineering concerned with the design, construction and science of aircraft and spacecraft. It is divided into two major and overlapping branches: aeronautical engineering and astronautical engineering...
, among many other uses. Topologically, SO(3) is the real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
RP3, and it is often desirable to represent rotations by a set of three numbers, known as Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
(in numerous variants), both because this is conceptually simple, and because one can build a combination of three gimbal
Gimbal
A gimbal is a pivoted support that allows the rotation of an object about a single axis. A set of two gimbals, one mounted on the other with pivot axes orthogonal, may be used to allow an object mounted on the innermost gimbal to remain immobile regardless of the motion of its support...
s to produce rotations in three dimensions. Topologically this corresponds to a map from the 3-torus T3 of three angles to the real projective space RP3 of rotations, but this map does not have rank 3 at all points (formally because it cannot be a covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
, as the only (non-trivial) covering space is the hypersphere S3), and the phenomenon of the rank dropping to 2 at certain points is referred to in engineering as gimbal lock
Gimbal lock
Gimbal lock is the loss of one degree of freedom in a three-dimensional space that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space....
.

