
Whitney immersion theorem
Encyclopedia
In differential topology
, the Whitney immersion theorem states that for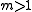 , any smooth
, any smooth 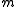 -dimensional manifold
-dimensional manifold
can be immersed in Euclidean
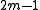 -space. Equivalently, every smooth
-space. Equivalently, every smooth 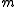 -dimensional manifold can be immersed in the
-dimensional manifold can be immersed in the 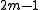 -dimensional sphere (this removes the
-dimensional sphere (this removes the 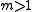 constraint).
constraint).
The weak version, for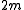 , is due to transversality (general position
, is due to transversality (general position
, dimension counting): two m-dimensional manifolds in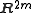 intersect generically in a 0-dimensional space.
intersect generically in a 0-dimensional space.
 where
where 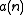 is the number of 1's that appear in the binary expansion of
is the number of 1's that appear in the binary expansion of  . In the same paper, Massey proved that for every n there is manifold (which happens to be a product of real projective spaces) that does not immerse in
. In the same paper, Massey proved that for every n there is manifold (which happens to be a product of real projective spaces) that does not immerse in 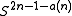 . The conjecture that every n-manifold immerses in
. The conjecture that every n-manifold immerses in 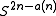 became known as the Immersion Conjecture which was eventually solved in the affirmative by Ralph Cohen .
became known as the Immersion Conjecture which was eventually solved in the affirmative by Ralph Cohen .
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, the Whitney immersion theorem states that for
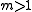 , any smooth
, any smooth 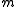 -dimensional manifold
-dimensional manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
can be immersed in Euclidean
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
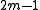 -space. Equivalently, every smooth
-space. Equivalently, every smooth 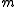 -dimensional manifold can be immersed in the
-dimensional manifold can be immersed in the 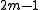 -dimensional sphere (this removes the
-dimensional sphere (this removes the 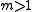 constraint).
constraint).The weak version, for
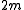 , is due to transversality (general position
, is due to transversality (general positionGeneral position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
, dimension counting): two m-dimensional manifolds in
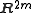 intersect generically in a 0-dimensional space.
intersect generically in a 0-dimensional space.Further Results
Massey went on to prove that every n-dimensional manifold is cobordant to a manifold that immerses in where
where 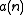 is the number of 1's that appear in the binary expansion of
is the number of 1's that appear in the binary expansion of  . In the same paper, Massey proved that for every n there is manifold (which happens to be a product of real projective spaces) that does not immerse in
. In the same paper, Massey proved that for every n there is manifold (which happens to be a product of real projective spaces) that does not immerse in 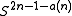 . The conjecture that every n-manifold immerses in
. The conjecture that every n-manifold immerses in 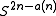 became known as the Immersion Conjecture which was eventually solved in the affirmative by Ralph Cohen .
became known as the Immersion Conjecture which was eventually solved in the affirmative by Ralph Cohen .External links
- Stiefel-Whitney Characteristic Classes and the Immersion Conjecture, by Jeffrey Giansiracusa, 2003
- Exposition of Cohen's work

