Calculus of functors
Encyclopedia
In algebraic topology
, a branch of mathematics
, the calculus of functors or Goodwillie calculus is a technique for studying functors by approximating them by a sequence of simpler functors; it generalizes the sheafification of a presheaf. This sequence of approximations is formally similar to the Taylor series
of a smooth function
, hence the term "calculus of functors".
Many objects of central interest in algebraic topology can be seen as functors, which are difficult to analyze directly, so the idea is to replace them with simpler functors which are sufficiently good approximations for certain purposes.
The calculus of functors was developed by Thomas Goodwillie in a series of three papers in the 1990s and 2000s, and has since been expanded and applied in a number of areas.
, is the functor of embedding
s of one manifold
M into another manifold N, whose first derivative in the sense of calculus of functors is the functor of immersions. As every embedding is an immersion, one obtains an inclusion of functors
– in this case the map from a functor to an approximation is an inclusion, but in general it is simply a map.
As this example illustrates, the linear approximation of a functor (on a topological space) is its sheafification, thinking of the functor as a presheaf on the space (formally, as a functor on the category of open subsets of the space), and sheaves are the linear functors.
This example was studied by Goodwillie and Michael Weiss.
One wishes to study a given functor
from the category of open spaces of a smooth manifold to topological spaces. In other words, space-valued presheaves on a smooth manifold. One wishes to know the topology of the space 
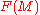for some input manifold 
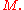One does this by approximating F by a sequence of functors 
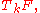together with natural transformations (maps of functors) 
These natural transforms are required to be compatible, meaning that the composition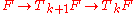 
equals the map 
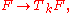and thus form a tower 
and can be thought of as "successive approximations", just as in a Taylor series one can progressively discard higher order terms.
The approximating functors are required to be "k-excisive
" – such polynomials are called polynomial functors by analogy with Taylor polynomials – which is the simplifying condition, and roughly means that they are determined by their behavior around k points at a time, or more formally are sheaves
on the configuration space
of k points in the given space. The difference between the kth and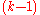
st functors is a "homogeneous functor of degree k" (by analogy with homogeneous polynomial
s), which can be classified.
For the functors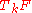
to be approximations to the original functor F, the resulting approximation maps 
must be n-connected
for some number n, meaning that the approximating functor approximates the original functor "in dimension up to n"; this may not occur. Further, if one wishes to reconstruct the original functor, the resulting approximations must be n-connected for n increasing to infinity. One then calls F an analytic functor, and says that "the Taylor tower converges to the functor", in analogy with Taylor series of an analytic function.
Homotopy calculus has seen far wider application than the other branches.
on links
of spheres in 1965, where he defined a "metastable range" in which the problem is simpler. This was identified as the quadratic approximation to the embeddings functor in Goodwillie and Weiss.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the calculus of functors or Goodwillie calculus is a technique for studying functors by approximating them by a sequence of simpler functors; it generalizes the sheafification of a presheaf. This sequence of approximations is formally similar to the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, hence the term "calculus of functors".
Many objects of central interest in algebraic topology can be seen as functors, which are difficult to analyze directly, so the idea is to replace them with simpler functors which are sufficiently good approximations for certain purposes.
The calculus of functors was developed by Thomas Goodwillie in a series of three papers in the 1990s and 2000s, and has since been expanded and applied in a number of areas.
Examples
A motivational example, of central interest in geometric topologyGeometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, is the functor of embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s of one manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M into another manifold N, whose first derivative in the sense of calculus of functors is the functor of immersions. As every embedding is an immersion, one obtains an inclusion of functors
– in this case the map from a functor to an approximation is an inclusion, but in general it is simply a map.As this example illustrates, the linear approximation of a functor (on a topological space) is its sheafification, thinking of the functor as a presheaf on the space (formally, as a functor on the category of open subsets of the space), and sheaves are the linear functors.
This example was studied by Goodwillie and Michael Weiss.
Definition
The precise details are quite technical, but the outline can easily be described.One wishes to study a given functor
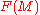from the category of open spaces of a smooth manifold to topological spaces. In other words, space-valued presheaves on a smooth manifold. One wishes to know the topology of the space for some input manifold 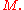One does this by approximating F by a sequence of functors 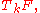together with natural transformations (maps of functors) These natural transforms are required to be compatible, meaning that the composition 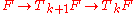equals the map 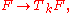and thus form a tower and can be thought of as "successive approximations", just as in a Taylor series one can progressively discard higher order terms.The approximating functors are required to be "k-excisive
Excision theorem
In algebraic topology, a branch of mathematics, the excision theorem is a useful theorem about relative homology—given topological spaces X and subspaces A and U such that U is also a subspace of A, the theorem says that under certain circumstances, we can cut out U from both spaces such...
" – such polynomials are called polynomial functors by analogy with Taylor polynomials – which is the simplifying condition, and roughly means that they are determined by their behavior around k points at a time, or more formally are sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of k points in the given space. The difference between the kth and
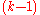st functors is a "homogeneous functor of degree k" (by analogy with homogeneous polynomialHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s), which can be classified.
For the functors
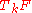to be approximations to the original functor F, the resulting approximation maps must be n-connectedN-connected
In the mathematical branch of algebraic topology, specifically homotopy theory, n-connectedness is a way to say that a space vanishes or that a map is an isomorphism "up to dimension n, in homotopy".-n-connected space:...
for some number n, meaning that the approximating functor approximates the original functor "in dimension up to n"; this may not occur. Further, if one wishes to reconstruct the original functor, the resulting approximations must be n-connected for n increasing to infinity. One then calls F an analytic functor, and says that "the Taylor tower converges to the functor", in analogy with Taylor series of an analytic function.
Branches
There are three branches of the calculus of functors, developed in the order:- manifold calculus, such as embeddings,
- homotopy calculus, and
- orthogonal calculus.
Homotopy calculus has seen far wider application than the other branches.
History
The notion of a sheaf and sheafification of a presheaf date to early category theory, and can be seen as the linear form of the calculus of functors. The quadratic form can be seen in the work of André HaefligerAndré Haefliger
André Haefliger is a Swiss mathematician who works primarily on topology.He studied mathematics in Lausanne. He received his PhD in 1958 from the University of Strasbourg under the supervision of Charles Ehresmann with "Structures feuilletées et cohomologie à valeurs dans un faisceau de...
on links
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
of spheres in 1965, where he defined a "metastable range" in which the problem is simpler. This was identified as the quadratic approximation to the embeddings functor in Goodwillie and Weiss.