
Poincaré complex
Encyclopedia
In mathematics, and especially topology
, a Poincaré complex (named after the mathematician Henri Poincaré
) is a generalisation of a manifold
.
The homology groups of a closed, orientable manifold are related in certain ways. This relationship came to be known as the Poincaré duality
. Poincaré duality gives an isomorphism between homology and cohomology groups. A topological space
X is called a Poincaré complex if its homology groups behave, in an informal sense, in the same way as the homology groups of a closed
, orientable manifold.
A Poincaré complex is a space where we assume Poincaré duality as an axiom
.
, and assume that the homology groups of C are finitely generated
. Assume that there exists a map , called a chain-diagonal, with the property that ; where the map denotes the ring homomorphism
known as the augmentation map
. It is defined as follows: if then
Using the diagonal as defined above, we are able to form pairings, namely: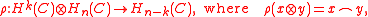
where denotes the cap product
denotes the cap product
. A chain complex C is called geometric if a chain-homotopy
exists between Δ and τΔ, where is given by
A geometric chain complex is called an algebraic Poincaré complex, of dimension n, if there exists an infinite-order
ed element of the n-dimensional homology group, say , such that the maps given by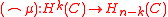
are group isomorphism
s for all . These isomorphisms are the isomorphisms of Poincaré duality.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a Poincaré complex (named after the mathematician Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
) is a generalisation of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
The homology groups of a closed, orientable manifold are related in certain ways. This relationship came to be known as the Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
. Poincaré duality gives an isomorphism between homology and cohomology groups. A topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is called a Poincaré complex if its homology groups behave, in an informal sense, in the same way as the homology groups of a closed
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
, orientable manifold.
A Poincaré complex is a space where we assume Poincaré duality as an axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
.
Definition
Let } be a chain complexChain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
, and assume that the homology groups of C are finitely generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
. Assume that there exists a map , called a chain-diagonal, with the property that ; where the map denotes the ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
known as the augmentation map
Augmentation ideal
In algebra, an augmentation ideal is an ideal that can be defined in any group ring. If G is a group and R a commutative ring, there is a ring homomorphism \varepsilon, called the augmentation map, from the group ring...
. It is defined as follows: if then
Using the diagonal as defined above, we are able to form pairings, namely:
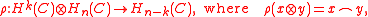
where
 denotes the cap product
denotes the cap productCap product
In algebraic topology the cap product is a method of adjoining a chain of degree p with a cochain of degree q, such that q ≤ p, to form a composite chain of degree p − q. It was introduced by Eduard Čech in 1936, and independently by Hassler Whitney in 1938.-Definition:Let X be a topological...
. A chain complex C is called geometric if a chain-homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
exists between Δ and τΔ, where is given by
A geometric chain complex is called an algebraic Poincaré complex, of dimension n, if there exists an infinite-order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
ed element of the n-dimensional homology group, say , such that the maps given by
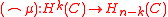
are group isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s for all . These isomorphisms are the isomorphisms of Poincaré duality.
Example
- The singularSingular homologyIn algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
chain complexChain complexIn mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
of an orientable, closed manifold is an example of a Poincaré complex,

