De Rham cohomology
Encyclopedia
In mathematics
, de Rham cohomology (after Georges de Rham
) is a tool belonging both to algebraic topology
and to differential topology
, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes. It is a cohomology theory based on the existence of differential form
s with prescribed properties.
as the differential.
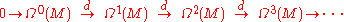
where Ω0(M) is the space of smooth functions on M, Ω1(M) is the space of 1-forms, and so forth. Forms which are the image of other forms under the exterior derivative are called exact and forms
whose exterior derivative is 0 are called closed (see closed and exact differential forms
); the relationship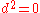
then says that exact forms are closed.
The converse, however, is not in general true; closed forms need not be exact. A simple but significant case is the 1-form of angle measure on the unit circle
, written conventionally as dθ. There is no actual function θ defined on the whole circle for which this is true; the increment of 2π in going once round the circle in the positive direction means that we can't take a single-valued θ. We can, however, change the topology by removing just one point.
The idea of de Rham cohomology is to classify the different types of closed forms on a manifold. One performs this classification by saying that two closed forms α and β in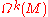
are cohomologous if they differ by an exact form, that is, if 
is exact. This classification induces an equivalence relation on the space of closed forms in 
. One then defines the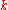 
-th de Rham cohomology group 
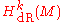to be the set of equivalence classes, that is, the set of closed forms in 
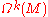modulo the exact forms.
Note that, for any manifold M with n connected components
This follows from the fact that any smooth function on M with zero derivative (i.e. locally constant) is constant on each of the connected components of M.
invariant. While the computation is not given, the following are the computed de Rham cohomologies for some common topological objects:
The n-sphere:
For the n-sphere, and also when taken together with a product of open intervals, we have the following. Let n > 0, m ≥ 0, and I an open real interval. Then
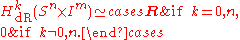
The n-torus:
Similarly, allowing n > 0 here, we obtain
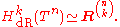
Punctured Euclidean space:
Punctured Euclidean space is simply Euclidean space
with the origin removed. For n > 0, we have:
The Möbius strip, M:
This more-or-less follows from the fact that the Möbius strip
may be, loosely speaking, "contracted" to the 1-sphere:
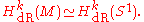
is an expression of duality
between de Rham cohomology and the homology
of chains. It says that the pairing of differential forms and chains, via integration, gives a homomorphism from de Rham cohomology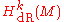
to singular cohomology groups Hk(M; R). De Rham's theorem, proved by Georges de Rham
in 1931, states that for a smooth manifold M, this map is in fact an isomorphism.
The wedge product endows the direct sum of these groups with a ring
structure. A further result of the theorem is that the two cohomology rings are isomorphic (as graded rings), where the analogous product on singular cohomology is the cup product
.
H*(U,F), where F is the sheaf
of abelian group
s determined by F(U) = R for all connected open sets U in M, and for open sets U and V such that U ⊂ V, the group morphism resV,U : F(V) → F(U) is given by the identity map on R, and where U is a good open cover of M (i.e. all the open sets in the open cover U are contractible
to a point, and all finite intersections of sets in U are either empty or contractible to a point).
Stated another way, if M is a compact Cm+1 manifold of dimension m, then for each k≤m, there is an isomorphism
where the left-hand side is the k-th de Rham cohomology group and the right-hand side is the Čech cohomology for the constant sheaf
with fibre R.
of k-forms on M (with Ω0 the sheaf of Cm + 1 functions on M). By the Poincaré lemma, the following sequence of sheaves is exact (in the category
of sheaves):
This sequence now breaks up into short exact sequences
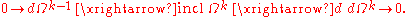
Each of these induces a long exact sequence in cohomology.
Since the sheaf of Cm + 1 functions on a manifold admits partitions of unity, the sheaf-cohomology Hi(Ωk) vanishes for i>0. So the long exact cohomology sequences themselves ultimately separate into a chain of isomorphisms. At one end of the chain is the Čech cohomology and at the other lies the de Rham cohomology.
, Hodge theory
, and the Atiyah-Singer index theorem. However, even in more classical contexts, the theorem has inspired a number of developments. Firstly, the Hodge theorem proves that there is an isomorphism between the cohomology consisting of harmonic forms and the de Rham cohomology consisting of closed forms modulo exact forms. This relies on an appropriate definition of harmonic forms and of the Hodge theorem. For further details see Hodge theory
.
is a compact
Riemannian manifold
, then each equivalence class in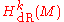
contains exactly one harmonic form. That is, every member ω of a given equivalence class of closed forms can be written as
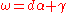
where
is some form, and γ is harmonic: Δγ=0.
Any harmonic function
on a compact connected Riemannian manifold is a constant. Thus, this particular representative element can be understood to be an extremum (a minimum) of all cohomologously equivalent forms on the manifold. For example, on a 2-torus
, one may envision a constant 1-form as one where all of the "hair" is combed neatly in the same direction (and all of the "hair" having the same length). In this case, there are two cohomologically distinct combings; all of the others are linear combinations. In particular, this implies that the 1st Betti number
of a two-torus is two. More generally, on an n-dimensional torus Tn, one can consider the various combings of k-forms on the torus. There are n choose k such combings that can be used to form the basis vectors for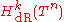
; the k-th Betti number for the de Rham cohomology group for the n-torus is thus n choose k.
More precisely, for a differential manifold M, one may equip it with some auxiliary Riemannian metric. Then the Laplacian Δ is defined by
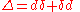
with d the exterior derivative
and δ the codifferential. The Laplacian is a homogeneous (in grading
) linear
differential operator
acting upon the exterior algebra
of differential form
s: we can look at its action on each component of degree k separately.
If M is compact
and oriented, the dimension
of the kernel
of the Laplacian acting upon the space of k-form
s is then equal (by Hodge theory
) to that of the de Rham cohomology group in degree k: the Laplacian picks out a unique harmonic form in each cohomology class of closed forms. In particular, the space of all harmonic k-forms on M is isomorphic to Hk(M;R). The dimension of each such space is finite, and is given by the k-th Betti number
.
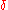be the codifferential, one says that a form 
is co-closed if 
and co-exact if 
for some form 
. The Hodge decomposition states that any k-form can be split into three L2
components:
where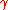
is harmonic: 
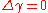. This follows by noting that exact and co-exact forms are orthogonal; the orthogonal complement then consists of forms that are both closed and co-closed: that is, of harmonic forms. Here, orthogonality is defined with respect to the L2
inner product on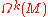
:
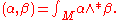
A precise definition and proof of the decomposition requires the problem to be formulated on Sobolev space
s. The idea here is that a Sobolev space provides the natural setting for both the idea of square-integrability and the idea of differentiation. This language helps overcome some of the limitations of requiring compact support.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, de Rham cohomology (after Georges de Rham
Georges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
) is a tool belonging both to algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and to differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes. It is a cohomology theory based on the existence of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s with prescribed properties.
Definition
The de Rham complex is the cochain complex of exterior differential forms on some smooth manifold M, with the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
as the differential.
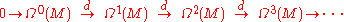
where Ω0(M) is the space of smooth functions on M, Ω1(M) is the space of 1-forms, and so forth. Forms which are the image of other forms under the exterior derivative are called exact and forms
whose exterior derivative is 0 are called closed (see closed and exact differential forms
Closed and exact differential forms
In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
); the relationship
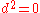then says that exact forms are closed.The converse, however, is not in general true; closed forms need not be exact. A simple but significant case is the 1-form of angle measure on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, written conventionally as dθ. There is no actual function θ defined on the whole circle for which this is true; the increment of 2π in going once round the circle in the positive direction means that we can't take a single-valued θ. We can, however, change the topology by removing just one point.
The idea of de Rham cohomology is to classify the different types of closed forms on a manifold. One performs this classification by saying that two closed forms α and β in
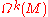are cohomologous if they differ by an exact form, that is, if is exact. This classification induces an equivalence relation on the space of closed forms in . One then defines the 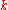-th de Rham cohomology group 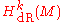to be the set of equivalence classes, that is, the set of closed forms in 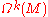modulo the exact forms.Note that, for any manifold M with n connected components
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
This follows from the fact that any smooth function on M with zero derivative (i.e. locally constant) is constant on each of the connected components of M.
De Rham cohomology computed
One may often find the general de Rham cohomologies of a manifold using the above fact about the zero cohomology and a Mayer–Vietoris sequence. Another useful fact is that the de Rham cohomology is a homotopyHomotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
invariant. While the computation is not given, the following are the computed de Rham cohomologies for some common topological objects:
The n-sphere:
For the n-sphere, and also when taken together with a product of open intervals, we have the following. Let n > 0, m ≥ 0, and I an open real interval. Then
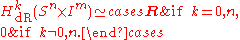
The n-torus:
Similarly, allowing n > 0 here, we obtain
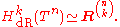
Punctured Euclidean space:
Punctured Euclidean space is simply Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
with the origin removed. For n > 0, we have:
 |
 |
 |
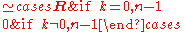The Möbius strip, M:
This more-or-less follows from the fact that the Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
may be, loosely speaking, "contracted" to the 1-sphere:
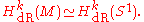
De Rham's theorem
Stokes' theoremStokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
is an expression of duality
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
between de Rham cohomology and the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of chains. It says that the pairing of differential forms and chains, via integration, gives a homomorphism from de Rham cohomology
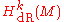to singular cohomology groups Hk(M; R). De Rham's theorem, proved by Georges de RhamGeorges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
in 1931, states that for a smooth manifold M, this map is in fact an isomorphism.
The wedge product endows the direct sum of these groups with a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
structure. A further result of the theorem is that the two cohomology rings are isomorphic (as graded rings), where the analogous product on singular cohomology is the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
.
Sheaf-theoretic de Rham isomorphism
The de Rham cohomology is isomorphic to the Čech cohomologyCech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
H*(U,F), where F is the sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s determined by F(U) = R for all connected open sets U in M, and for open sets U and V such that U ⊂ V, the group morphism resV,U : F(V) → F(U) is given by the identity map on R, and where U is a good open cover of M (i.e. all the open sets in the open cover U are contractible
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
to a point, and all finite intersections of sets in U are either empty or contractible to a point).
Stated another way, if M is a compact Cm+1 manifold of dimension m, then for each k≤m, there is an isomorphism
where the left-hand side is the k-th de Rham cohomology group and the right-hand side is the Čech cohomology for the constant sheaf
Constant sheaf
In mathematics, the constant sheaf on a topological space X associated to a set A is a sheaf of sets on X whose stalks are all equal to A. It is denoted by or AX. The constant presheaf with value A is the presheaf that assigns to each open subset of X the value A, and all of whose restriction maps...
with fibre R.
Proof
Let Ωk denote the sheaf of germsSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of k-forms on M (with Ω0 the sheaf of Cm + 1 functions on M). By the Poincaré lemma, the following sequence of sheaves is exact (in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of sheaves):
This sequence now breaks up into short exact sequences
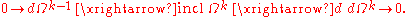
Each of these induces a long exact sequence in cohomology.
Since the sheaf of Cm + 1 functions on a manifold admits partitions of unity, the sheaf-cohomology Hi(Ωk) vanishes for i>0. So the long exact cohomology sequences themselves ultimately separate into a chain of isomorphisms. At one end of the chain is the Čech cohomology and at the other lies the de Rham cohomology.
Related ideas
The de Rham cohomology has inspired many mathematical ideas, including Dolbeault cohomologyDolbeault cohomology
In mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold...
, Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
, and the Atiyah-Singer index theorem. However, even in more classical contexts, the theorem has inspired a number of developments. Firstly, the Hodge theorem proves that there is an isomorphism between the cohomology consisting of harmonic forms and the de Rham cohomology consisting of closed forms modulo exact forms. This relies on an appropriate definition of harmonic forms and of the Hodge theorem. For further details see Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
.
Harmonic forms
If is a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, then each equivalence class in
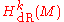contains exactly one harmonic form. That is, every member ω of a given equivalence class of closed forms can be written as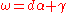where
is some form, and γ is harmonic: Δγ=0.Any harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
on a compact connected Riemannian manifold is a constant. Thus, this particular representative element can be understood to be an extremum (a minimum) of all cohomologously equivalent forms on the manifold. For example, on a 2-torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, one may envision a constant 1-form as one where all of the "hair" is combed neatly in the same direction (and all of the "hair" having the same length). In this case, there are two cohomologically distinct combings; all of the others are linear combinations. In particular, this implies that the 1st Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
of a two-torus is two. More generally, on an n-dimensional torus Tn, one can consider the various combings of k-forms on the torus. There are n choose k such combings that can be used to form the basis vectors for
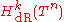; the k-th Betti number for the de Rham cohomology group for the n-torus is thus n choose k.More precisely, for a differential manifold M, one may equip it with some auxiliary Riemannian metric. Then the Laplacian Δ is defined by
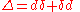
with d the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
and δ the codifferential. The Laplacian is a homogeneous (in grading
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
) linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
acting upon the exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s: we can look at its action on each component of degree k separately.
If M is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and oriented, the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the Laplacian acting upon the space of k-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s is then equal (by Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
) to that of the de Rham cohomology group in degree k: the Laplacian picks out a unique harmonic form in each cohomology class of closed forms. In particular, the space of all harmonic k-forms on M is isomorphic to Hk(M;R). The dimension of each such space is finite, and is given by the k-th Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
.
Hodge decomposition
Letting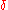 be the codifferential, one says that a form is co-closed if and co-exact if for some form . The Hodge decomposition states that any k-form can be split into three L2Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
components:
where
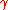is harmonic: 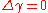. This follows by noting that exact and co-exact forms are orthogonal; the orthogonal complement then consists of forms that are both closed and co-closed: that is, of harmonic forms. Here, orthogonality is defined with respect to the L2Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
inner product on
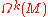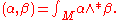
:A precise definition and proof of the decomposition requires the problem to be formulated on Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s. The idea here is that a Sobolev space provides the natural setting for both the idea of square-integrability and the idea of differentiation. This language helps overcome some of the limitations of requiring compact support.