Partition of unity
Encyclopedia
In mathematics
, a partition of unity of a topological space
X is a set of continuous functions,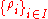
, from X to the unit interval
[0,1] such that for every point,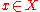
,
Sometimes, the requirement is not as strict: the sum of all the function values at a particular point is only required to be positive rather than a fixed number for all points in the space
Partitions of unity are useful because they often allow one to extend local constructions to the whole space.
The existence of partitions of unity assumes two distinct forms:
Thus one chooses either to have the supports
indexed by the open cover, or the supports compact. If the space is compact
, then there exist partitions satisfying both requirements.
Paracompactness
of the space is a necessary condition to guarantee the existence of a partition of unity subordinate to any open cover
. Depending on the category
which the space belongs to, it may also be a sufficient condition. The construction uses mollifier
s (bump functions), which exist in the continuous and smooth
manifold
categories, but not the analytic category. Thus analytic partitions of unity do not exist. See analytic continuation
.
) of a function defined over a manifold: One first defines the integral of a function whose support is contained in a single coordinate patch of the manifold; then one uses a partition of unity to define the integral of an arbitrary function; finally one shows that the definition is independent of the chosen partition of unity.
A partition of unity can be used to show the existence of a Riemannian metric on an arbitrary manifold.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a partition of unity of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is a set of continuous functions,
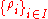, from X to the unit intervalUnit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1] such that for every point,
,
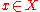- there is a neighbourhoodNeighbourhood (mathematics)In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of x where all but a finite number of the functions are 0, and - the sum of all the function values at x is 1, i.e.,
.
Sometimes, the requirement is not as strict: the sum of all the function values at a particular point is only required to be positive rather than a fixed number for all points in the space
The existence of partitions of unity assumes two distinct forms:
- Given any open cover {Ui}i∈I of a space, there exists a partition {ρi}i∈I indexed over the same set I such that suppSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
ρi⊆Ui. Such a partition is said to be subordinate to the open cover {Ui}i. - Given any open cover {Ui}i∈I of a space, there exists a partition {ρj}j∈J indexed over a possibly distinct index set J such that each ρj has compact support and for each j∈J, supp ρj⊆Ui for some i∈I.
Thus one chooses either to have the supports
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
indexed by the open cover, or the supports compact. If the space is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, then there exist partitions satisfying both requirements.
Paracompactness
Paracompact space
In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
of the space is a necessary condition to guarantee the existence of a partition of unity subordinate to any open cover
Paracompact space
In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
. Depending on the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
which the space belongs to, it may also be a sufficient condition. The construction uses mollifier
Mollifier
In mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
s (bump functions), which exist in the continuous and smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
categories, but not the analytic category. Thus analytic partitions of unity do not exist. See analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
.
Applications
A partition of unity can be used to define the integral (with respect to a volume formVolume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
) of a function defined over a manifold: One first defines the integral of a function whose support is contained in a single coordinate patch of the manifold; then one uses a partition of unity to define the integral of an arbitrary function; finally one shows that the definition is independent of the chosen partition of unity.
A partition of unity can be used to show the existence of a Riemannian metric on an arbitrary manifold.
External links
- General information on partition of unity at [Mathworld]
- Applications of a partition of unity at [Planet Math]