Mollifier
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, mollifiers (also known as approximations to the identity) are smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s with special properties, used in distribution theory
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
to create sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of smooth functions approximating nonsmooth (generalized) functions, via convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
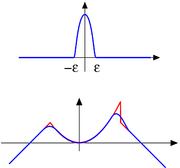
. Intuitively, given a function which is rather irregular, by convolving it with a mollifier the function gets "mollified", that is, its sharp features are smoothed, while still remaining close to the original nonsmooth function. They are also known as Friedrichs mollifiers after Kurt Otto Friedrichs, the
mathematician who introduced them.
History
Mollifiers were introduced by Kurt Otto Friedrichs in his paper , which is a watershed in the modern theory of partial differential equations. The name of the concept had a curious genesis: at that time Friedrichs was a colleague of the mathematician Donald Alexander Flanders, and since he liked to consult colleagues about English usage, he asked Flanders how to name the smoothing operator he was about to introduce. Flanders was a puritanPuritan
The Puritans were a significant grouping of English Protestants in the 16th and 17th centuries. Puritanism in this sense was founded by some Marian exiles from the clergy shortly after the accession of Elizabeth I of England in 1558, as an activist movement within the Church of England...
so his friends nicknamed him Moll after Moll Flanders
Moll Flanders
The Fortunes and Misfortunes of the Famous Moll Flanders is a novel written by Daniel Defoe in 1722, after his work as a journalist and pamphleteer. By 1722, Defoe had become a recognised novelist, with the success of Robinson Crusoe in 1719...
in recognition of his moral qualities, and he suggested to call the new mathematical concept a "mollifier" as a pun incorporating both Flanders' nickname and the verb 'to mollify', meaning 'to smooth over' in a figurative sense.
Sergei Sobolev had previously used mollifiers in his epoch making 1938 paper containing the proof of the Sobolev embedding theorem, as Friedrichs himself later acknowledged.
There is a little misunderstanding in the concept of mollifier: Friedrichs defined as "mollifier" the integral operator whose kernel is one of the functions nowadays called mollifiers. However, since the properties of an integral operator are completely determined by its kernel, the name mollfier was inherited by the kernel itself as a result of common usage.
Modern (distribution based) definition
. If
is a smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
on ℝn, n ≥ 1, satisfying the following three requirements
- it is compactly supportedSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
(such as a bump function) 
where
is the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
and the limit must be understood in the space of Schwartz distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s, then
is a mollifier. The function 
could satisfy also further conditions: for example, if it satisfies
≥ 0 for all x ∈ ℝn, then it is a positive mollifier
=
for some infinitely differentiable function 
: ℝ+ → ℝ, then it is a symmetric mollifier
Concrete example
Consider the functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
ℝn defined by
It is easily seen that this function is infinitely differentiable, non analytic
Non-analytic smooth function
In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth...
with vanishing derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
for
. Divide this function by its integral over the whole space to get a function 
of integral one, which can be used as mollifier as described above: it is also easy to see that 
defines a positive and symmetric mollifier.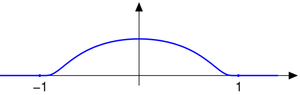
Properties
All properties of a mollifier are related to its behaviour under the operation of convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
: we list the following ones, whose proofs can be found in every text on distribution theory
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
.
Smoothing property
For any distribution
, the following sequence of convolutions indexed by the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
where
denotes convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
, is a sequence of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s.
Approximation of identity
For any distribution
, the following sequence of convolutions indexed by the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
converges to 
Support of convolution
For any distribution
,
where
indicates the support in the sense of distributions, and 
indicates their Minkowski additionMinkowski addition
In geometry, the Minkowski sum of two sets A and B in Euclidean space is the result of adding every element of A to every element of B, i.e...
.
Applications
The basic applications of mollifiers is to prove properties valid for smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s also in nonsmooth situations:
Product of distributions
In some theories of generalized functionGeneralized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s, mollifiers are used to define the multiplication of distributions: precisely, given two distributions
and 
, the limit of the product of a smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
and a distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
defines (if it exists) their product in various theories of generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s.
"Weak=Strong" theorems
Very informally, mollifiers are used to prove the identity of two different kind of extension of differential operators: the strong extension and the weak extensionWeak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
. The paper illustrates this concept quite well: however the high quantity of technical details needed to show what this really means prevent us from being formally detailed in this short description.
Smooth cutoff functions
By convolution of the characteristic function of the unit ball
with the smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
(defined as in with 
), one obtains the function
which is a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
equal to
on 
, with support contained in 
. This can be seen easily by observing that if 
and 
then 
. Hence for 
,
.It is easy to see how this construction can be generalized to obtain a smooth function identical to one on a neighbourhood of a given compact set, and equal to zero in every point whose distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
from this set is greater than a given
. Such a function is called a (smooth) cutoff function: those functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
are used to eliminate singularities of a given (generalized
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
) function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
by multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
. They leave unchanged the value of the (generalized
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
) function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
they multiply only on a given set, thus modifying its support: also cutoff functions are the basic parts of smooth partitions of unity.
See also
- Approximate identityApproximate identityIn functional analysis and ring theory, an approximate identity is a net in a Banach algebra or ring that acts as a substitute for an identity element....
- Bump function
- ConvolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
- Distribution (mathematics)Distribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
- Kurt Otto Friedrichs
- Generalized functionGeneralized functionIn mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
- Sergei Sobolev