Generalized function
Encyclopedia
In mathematics
, generalized functions are objects generalizing the notion of function
s. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth function
s, and (going to extremes) describing physical phenomena such as point charges. They are applied extensively, especially in physics
and engineering
.
A common feature of some of the approaches is that they build on operator aspects of everyday, numerical functions. The early history is connected with some ideas on operational calculus
, and more contemporary developments in certain directions are closely related to ideas of Mikio Sato
, on what he calls algebraic analysis
. Important influences on the subject have been the technical requirements of theories of partial differential equation
s, and group representation
theory.
, in the Laplace transform, and in Riemann's theory of trigonometric series, which were not necessarily the Fourier series
of an integrable function. These were disconnected aspects of mathematical analysis
at the time.
The intensive use of the Laplace transform in engineering led to the heuristic
use of symbolic methods, called operational calculus
. Since justifications were given that used divergent series
, these methods had a bad reputation from the point of view of pure mathematics
. They are typical of later application of generalized function methods. An influential book on operational calculus was Oliver Heaviside
's Electromagnetic Theory of 1899.
When the Lebesgue integral was introduced, there was for the first time a notion of generalized function central to mathematics. An integrable function, in Lebesgue's theory, is equivalent to any other which is the same almost everywhere
. That means its value at a given point is (in a sense) not its most important feature. In functional analysis
a clear formulation is given of the essential feature of an integrable function, namely the way it defines a linear functional
on other functions. This allows a definition of weak derivative
.
During the late 1920s and 1930s further steps were taken, basic to future work. The Dirac delta function
was boldly defined by Paul Dirac
(an aspect of his scientific formalism
); this was to treat measures
, thought of as densities (such as charge density
) like honest functions. Sergei Sobolev, working in partial differential equation theory, defined the first adequate theory of generalized functions, from the mathematical point of view, in order to work with weak solution
s of PDEs. Others proposing related theories at the time were Salomon Bochner
and Kurt Friedrichs. Sobolev's work was further developed in an extended form by L. Schwartz.
, developed by Laurent Schwartz
. It can be called a principled theory, based on duality theory
for topological vector space
s. Its main rival, in applied mathematics
, is to use sequences of smooth approximations (the 'James Lighthill
' explanation), which is more ad hoc. This now enters the theory as mollifier
theory.
This theory was very successful and is still widely used, but suffers from the main drawback that it allows only linear
operations. In other words, distributions cannot be multiplied (except for very special cases): unlike most classical function space
s, they are not an algebra
. For example it is not meaningful to square the Dirac delta function
. Work of Schwartz from around 1954 showed that this was an intrinsic difficulty.
Some solutions to the multiplication problem have been proposed. One is based on a very simple and intuitive definition a generalized function given by Yu. V. Egorov (see also his article in Demidov's book in the book list below) that allows arbitrary operations on, and between, generalized functions.
Another solution of the multiplication problem is dictated by the path integral formulation
of quantum mechanics
.
Since this is required to be equivalent to the Schrödinger theory of quantum mechanics
which is invariant under coordinate transformations, this property must be shared by path integrals. This fixes all products of generalized functions
as shown by H. Kleinert
and A. Chervyakov. The result is equivalent to what can be derived from
dimensional regularization
.
and those by E. Rosinger, Y. Egorov, and R. Robinson
.
In the first case, the multiplication is determined with some regularization of generalized function. In the second case, the algebra is constructed as multiplication of distributions. Both cases are discussed below.
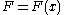to its smooth
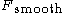and its singular 
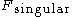parts. The product of generalized functions 
and 
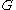appears as
.
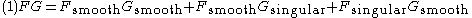Such a rule applies to both, the space of main functions and the space of operators which act on the space of the main functions.
The associativity of multiplication is achieved; and the function signum is defined in such a way, that its square is unity everywhere (including the origin of coordinates). Note that the product of singular parts does not appear in the right-hand side of (1); in particular,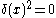
. Such a formalism includes the conventional theory of generalized functions (without their product) as a special case. However, the resulting algebra is non-commutative: generalized functions signum and delta anticommute.
Few applications of the algebra were suggested.
Various approaches are used today. The simplest one is based on the definition of generalized function given by Yu. V. Egorov (see ref. below). Another approach to construct associative differential algebra
s is based on J.-F. Colombeau's construction: see Colombeau algebra
. These are factor spaces
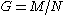
of "moderate" modulo "negligible" nets of functions, where "moderateness" and "negligibility" refers to growth with respect to the index of the family.
.
Then for any semi normed algebra (E,P), the factor space will be
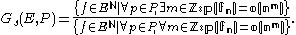
In particular, for (E, P)=(C,|.|) one gets (Colombeau's) generalized complex numbers (which can be "infinitely large" and "infinitesimally small" and still allow for rigorous arithmetics,
very similar to nonstandard numbers).
For (E, P) = (C∞(R),{pk})
(where pk is the supremum of all derivatives of order less than or equal to k on the ball of radius k)
one gets Colombeau's simplified algebra
.
where ∗ is the convolution
operation, and
This injection is non-canonical in the sense that it depends on the choice of the mollifier
φ, which should be C∞, of integral one and have all its derivatives at 0 vanishing. To obtain a canonical injection, the indexing set can be modified to be N × D(R),
with a convenient filter base on D(R) (functions of vanishing moment
s up to order q).
of semi normed algebras on some topological space X, then Gs(E, P) will also have this property.
This means that the notion of restriction will be defined, which allows to define the support
of a generalized function w.r.t. a subsheaf, in particular:
's wave front set
also for generalized functions.
This has an especially important application in the analysis of
propagation
of singularities
.
, based on the field of fractions
of convolution
algebras that are integral domains; and the theories of hyperfunction
s, based (in their initial conception) on boundary values of analytic function
s, and now making use of sheaf theory.
s that goes beyond the manifold
s that are the typical function domains. The applications are mostly in number theory
, particularly to adelic algebraic group
s. André Weil
rewrote Tate's thesis
in this language, characterizing the zeta distribution on the idele group; and has also applied it to the explicit formula of an L-function.
. This is on the Schwartz pattern, constructing objects dual to the test objects, smooth sections of a bundle that have compact support. The most developed theory is that of De Rham currents, dual to differential form
s. These are homological in nature, in the way that differential forms give rise to De Rham cohomology
. They can be used to formulate a very general Stokes' theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, generalized functions are objects generalizing the notion of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s, and (going to extremes) describing physical phenomena such as point charges. They are applied extensively, especially in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
.
A common feature of some of the approaches is that they build on operator aspects of everyday, numerical functions. The early history is connected with some ideas on operational calculus
Operational calculus
Operational calculus, also known as operational analysis, is a technique by which problems in analysis, in particular differential equations, are transformed into algebraic problems, usually the problem of solving a polynomial equation.-History:...
, and more contemporary developments in certain directions are closely related to ideas of Mikio Sato
Mikio Sato
is a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
, on what he calls algebraic analysis
Algebraic analysis
Algebraic analysis is an area of mathematics that deals with systems of linear partial differential equations by using sheaf theory and complex analysis to study properties and generalizations of functions such as hyperfunctions and microfunctions.-See also:...
. Important influences on the subject have been the technical requirements of theories of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, and group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
theory.
Some early history
In the mathematics of the nineteenth century, aspects of generalized function theory appeared, for example in the definition of the Green's functionGreen's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
, in the Laplace transform, and in Riemann's theory of trigonometric series, which were not necessarily the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of an integrable function. These were disconnected aspects of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
at the time.
The intensive use of the Laplace transform in engineering led to the heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
use of symbolic methods, called operational calculus
Operational calculus
Operational calculus, also known as operational analysis, is a technique by which problems in analysis, in particular differential equations, are transformed into algebraic problems, usually the problem of solving a polynomial equation.-History:...
. Since justifications were given that used divergent series
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
, these methods had a bad reputation from the point of view of pure mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
. They are typical of later application of generalized function methods. An influential book on operational calculus was Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
's Electromagnetic Theory of 1899.
When the Lebesgue integral was introduced, there was for the first time a notion of generalized function central to mathematics. An integrable function, in Lebesgue's theory, is equivalent to any other which is the same almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. That means its value at a given point is (in a sense) not its most important feature. In functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
a clear formulation is given of the essential feature of an integrable function, namely the way it defines a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on other functions. This allows a definition of weak derivative
Weak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
.
During the late 1920s and 1930s further steps were taken, basic to future work. The Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
was boldly defined by Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
(an aspect of his scientific formalism
Scientific formalism
Scientific formalism is a broad term for a family of approaches to the presentation of science. It is viewed as an important part of the scientific method, especially in the physical sciences.-Levels of formalism:...
); this was to treat measures
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, thought of as densities (such as charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
) like honest functions. Sergei Sobolev, working in partial differential equation theory, defined the first adequate theory of generalized functions, from the mathematical point of view, in order to work with weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
s of PDEs. Others proposing related theories at the time were Salomon Bochner
Salomon Bochner
Salomon Bochner was an American mathematician of Austrian-Hungarian origin, known for wide-ranging work in mathematical analysis, probability theory and differential geometry.- Life :...
and Kurt Friedrichs. Sobolev's work was further developed in an extended form by L. Schwartz.
Schwartz distributions
The realization of such a concept that was to become accepted as definitive, for many purposes, was the theory of distributionsDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, developed by Laurent Schwartz
Laurent Schwartz
Laurent-Moïse Schwartz was a French mathematician. He pioneered the theory of distributions, which gives a well-defined meaning to objects such as the Dirac delta function. He was awarded the Fields medal in 1950 for his work...
. It can be called a principled theory, based on duality theory
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
for topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s. Its main rival, in applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, is to use sequences of smooth approximations (the 'James Lighthill
James Lighthill
Sir Michael James Lighthill, FRS was a British applied mathematician, known for his pioneering work in the field of aeroacoustics.-Biography:...
' explanation), which is more ad hoc. This now enters the theory as mollifier
Mollifier
In mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
theory.
This theory was very successful and is still widely used, but suffers from the main drawback that it allows only linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
operations. In other words, distributions cannot be multiplied (except for very special cases): unlike most classical function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s, they are not an algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. For example it is not meaningful to square the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. Work of Schwartz from around 1954 showed that this was an intrinsic difficulty.
Some solutions to the multiplication problem have been proposed. One is based on a very simple and intuitive definition a generalized function given by Yu. V. Egorov (see also his article in Demidov's book in the book list below) that allows arbitrary operations on, and between, generalized functions.
Another solution of the multiplication problem is dictated by the path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Since this is required to be equivalent to the Schrödinger theory of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
which is invariant under coordinate transformations, this property must be shared by path integrals. This fixes all products of generalized functions
as shown by H. Kleinert
Hagen Kleinert
Hagen Kleinert is Professor of Theoretical Physics at the Free University of Berlin, Germany , at theWest University of Timişoara, at thein Bishkek. He is also of the...
and A. Chervyakov. The result is equivalent to what can be derived from
dimensional regularization
Dimensional regularization
In theoretical physics, dimensional regularization is a method introduced by Giambiagi and Bollini for regularizing integrals in the evaluation of Feynman diagrams; in other words, assigning values to them that are meromorphic functions of an auxiliary complex parameter d, called the...
.
Algebras of generalized functions
Several constructions of algebras of generalized functions have been proposed, among others those by Yu. M. Shirokovand those by E. Rosinger, Y. Egorov, and R. Robinson
.
In the first case, the multiplication is determined with some regularization of generalized function. In the second case, the algebra is constructed as multiplication of distributions. Both cases are discussed below.
Non-commutative algebra of generalized functions
The algebra of generalized functions can be built-up with an appropriate procedure of projection of a function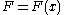 to its smooth 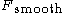and its singular 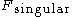parts. The product of generalized functions and 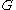appears as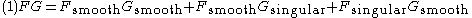.Such a rule applies to both, the space of main functions and the space of operators which act on the space of the main functions.
The associativity of multiplication is achieved; and the function signum is defined in such a way, that its square is unity everywhere (including the origin of coordinates). Note that the product of singular parts does not appear in the right-hand side of (1); in particular,
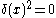. Such a formalism includes the conventional theory of generalized functions (without their product) as a special case. However, the resulting algebra is non-commutative: generalized functions signum and delta anticommute.Few applications of the algebra were suggested.
Multiplication of distributions
The problem of multiplication of distributions, a limitation of the Schwartz distribution theory, becomes serious for non-linear problems.Various approaches are used today. The simplest one is based on the definition of generalized function given by Yu. V. Egorov (see ref. below). Another approach to construct associative differential algebra
Differential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
s is based on J.-F. Colombeau's construction: see Colombeau algebra
Colombeau algebra
In mathematics, the Colombeau algebra is an algebra introduced with the aim of constructing an improved theory of distributions in which multiplication is not problematic...
. These are factor spaces
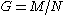
of "moderate" modulo "negligible" nets of functions, where "moderateness" and "negligibility" refers to growth with respect to the index of the family.
Example: Colombeau algebra
A simple example is obtained by using the polynomial scale on N,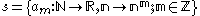.Then for any semi normed algebra (E,P), the factor space will be
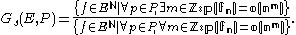
In particular, for (E, P)=(C,|.|) one gets (Colombeau's) generalized complex numbers (which can be "infinitely large" and "infinitesimally small" and still allow for rigorous arithmetics,
very similar to nonstandard numbers).
For (E, P) = (C∞(R),{pk})
(where pk is the supremum of all derivatives of order less than or equal to k on the ball of radius k)
one gets Colombeau's simplified algebra
Colombeau algebra
In mathematics, the Colombeau algebra is an algebra introduced with the aim of constructing an improved theory of distributions in which multiplication is not problematic...
.
Injection of Schwartz distributions
This algebra "contains" all distributions T of D' via the injection- j(T) = (φn ∗ T)n + N,
where ∗ is the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
operation, and
- φn(x) = n φ(nx).
This injection is non-canonical in the sense that it depends on the choice of the mollifier
Mollifier
In mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
φ, which should be C∞, of integral one and have all its derivatives at 0 vanishing. To obtain a canonical injection, the indexing set can be modified to be N × D(R),
with a convenient filter base on D(R) (functions of vanishing moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
s up to order q).
Sheaf structure
If (E,P) is a (pre-)sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of semi normed algebras on some topological space X, then Gs(E, P) will also have this property.
This means that the notion of restriction will be defined, which allows to define the support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of a generalized function w.r.t. a subsheaf, in particular:
- For the subsheaf {0}, one gets the usual support (complement of the largest open subset where the function is zero).
- For the subsheaf E (embedded using the canonical (constant) injection), one gets what is called the singular support, i.e., roughly speaking, the closure of the set where the generalized function is not a smooth function (for E = C∞).
Microlocal analysis
The Fourier transformation being (well-)defined for compactly supported generalized functions (component-wise), one can apply the same construction as for distributions, and define Lars HörmanderLars Hörmander
Lars Valter Hörmander is a Swedish mathematician who has been called "the foremost contributor to the modern theory of linear partial differential equations". He was awarded the Fields Medal in 1962, and the Wolf Prize in 1988...
's wave front set
Wave front set
In mathematical analysis, more precisely in microlocal analysis, the wave front WF characterizes the singularities of a generalized function f, not only in space, but also with respect to its Fourier transform at each point...
also for generalized functions.
This has an especially important application in the analysis of
propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
of singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
.
Other theories
These include: the convolution quotient theory of Jan MikusinskiJan Mikusinski
Prof. Jan Mikusiński was a Polish mathematician known for his pioneering work in mathematical analysis. Mikusiński developed an operational calculus - 44A40 Calculus of Mikusiński, which is relevant for solving differential equations...
, based on the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
algebras that are integral domains; and the theories of hyperfunction
Hyperfunction
In mathematics, hyperfunctions are generalizations of functions, as a 'jump' from one holomorphic function to another at a boundary, and can be thought of informally as distributions of infinite order...
s, based (in their initial conception) on boundary values of analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s, and now making use of sheaf theory.
Topological groups
Bruhat introduced a class of test functions, the Schwartz–Bruhat functions as they are now known, on a class of locally compact groupLocally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s that goes beyond the manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s that are the typical function domains. The applications are mostly in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, particularly to adelic algebraic group
Adelic algebraic group
In abstract algebra, an adelic algebraic group is a topological group defined by an algebraic group G over a number field K, and the adele ring A = A of K. It consists of the points of G having values in A; the definition of the appropriate topology is straightforward only in case G is a linear...
s. André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
rewrote Tate's thesis
Tate's thesis
In number theory, Tate's thesis is the thesis of where he reformulated the work of Erich Hecke on L-series in terms of Fourier analysis on adelic groups....
in this language, characterizing the zeta distribution on the idele group; and has also applied it to the explicit formula of an L-function.
Generalized section
A further way in which the theory has been extended is as generalized sections of a smooth vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
. This is on the Schwartz pattern, constructing objects dual to the test objects, smooth sections of a bundle that have compact support. The most developed theory is that of De Rham currents, dual to differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s. These are homological in nature, in the way that differential forms give rise to De Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
. They can be used to formulate a very general Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
.
See also
- rigged Hilbert spaceRigged Hilbert spaceIn mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
- generalized eigenfunction
- Distribution (mathematics)Distribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
- Beppo-Levi space
Books
- L. Schwartz: Théorie des distributions
- L. Schwartz: Sur l'impossibilité de la multiplication des distributions. Comptes Rendus de L'Academie des Sciences, Paris, 239 (1954) 847-848.
- I.M. Gel'fand et al.: Generalized Functions, vols I–VI, Academic Press, 1964–. (Translated from Russian.)
- L. Hörmander: The Analysis of Linear Partial Differential Operators, Springer Verlag, 1983.
- A. S. Demidov: Generalized Functions in Mathematical Physics: Main Ideas and Concepts (Nova Science Publishers, Huntington, 2001). With an addition by Yu. V. Egorov.
- M. Oberguggenberger: Multiplication of distributions and applications to partial differential equations (Longman, Harlow, 1992).
- M. Oberguggenberger: Generalized functions in nonlinear models - a survey. Nonlinear Analysis 47(8) (2001), 5029-5040 online here.
- J.-F. ColombeauColombeau algebraIn mathematics, the Colombeau algebra is an algebra introduced with the aim of constructing an improved theory of distributions in which multiplication is not problematic...
: New Generalized Functions and Multiplication of Distributions, North Holland, 1983. - M. Grosser et al.: Geometric theory of generalized functions with applications to general relativity, Kluwer Academic Publishers, 2001.
- H. KleinertHagen KleinertHagen Kleinert is Professor of Theoretical Physics at the Free University of Berlin, Germany , at theWest University of Timişoara, at thein Bishkek. He is also of the...
, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2006)(also available online here ). See Chapter 11 for products of generalized functions.