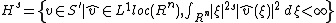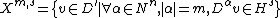Beppo-Levi space
Encyclopedia
In functional analysis
, a branch of mathematics, a Beppo-Levi space, named after Beppo Levi
, is a certain space of generalized function
s.
In the following,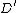 is the space of distributions
is the space of distributions
,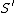 is the space of tempered distributions in
is the space of tempered distributions in 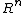 ,
,  the differentiation operator with
the differentiation operator with  a multi-index, and
a multi-index, and 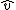 is the Fourier transform
is the Fourier transform
of .
.
The Beppo-Levi space is
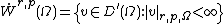
( denotes the Sobolev
denotes the Sobolev
semi-norm)
An alternative definition is:
Given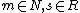 such that
such that
Let
Then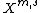 denotes the Beppo-Levi space
denotes the Beppo-Levi space
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a branch of mathematics, a Beppo-Levi space, named after Beppo Levi
Beppo Levi
Beppo Levi was an Italian mathematician. He published high-level academic articles and books not only in mathematics, but also in physics, history, philosophy, and pedagogy. Levi was a member of the Bologna Academy of Sciences and of the Accademia dei Lincei.- Early years :Beppo Levi was born on...
, is a certain space of generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s.
In the following,
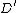 is the space of distributions
is the space of distributionsDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
,
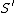 is the space of tempered distributions in
is the space of tempered distributions in 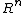 ,
,  the differentiation operator with
the differentiation operator with  a multi-index, and
a multi-index, and 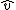 is the Fourier transform
is the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of
 .
.The Beppo-Levi space is
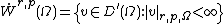
(
 denotes the Sobolev
denotes the SobolevSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
semi-norm)
An alternative definition is:
Given
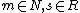 such that
such thatLet
Then
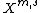 denotes the Beppo-Levi space
denotes the Beppo-Levi space