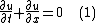Weak solution
Encyclopedia
In mathematics
, a weak solution (also called a generalized solution) to an ordinary
or partial differential equation
is a function
for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for different classes of equations. One of the most important is based on the notion of distributions
.
Avoiding the language of distributions, one starts with a differential equation and rewrites it in such a way that no derivatives of the solution of the equation show up (the new form is called the weak formulation
, and the solutions to it are called weak solutions). Somewhat surprisingly, a differential equation may have solutions which are not differentiable; and the weak formulation allows one to find such solutions.
Weak solutions are important because a great many differential equations encountered in modelling real world phenomena do not admit sufficiently smooth solutions and then the only way of solving such equations is using the weak formulation. Even in situations where an equation does have differentiable solutions, it is often convenient to first prove the existence of weak solutions and only later show that those solutions are in fact smooth enough.
(see partial derivative
for the notation) where u = u(t, x) is a function of two real
variables. Assume that u is continuously differentiable on the Euclidean space
R2, multiply this equation (1) by a smooth function
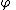of compact support, and integrate. One obtains
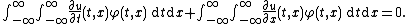
Using Fubini's theorem
which allows one to interchange the order of integration, as well as integration by parts
(in t for the first term and in x for the second term) this equation becomes
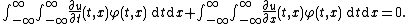
(Notice that while the integrals go from −∞ to ∞, the integrals are essentially over a finite box because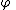
has compact support, and it is this observation which also allows for integration by parts without the introduction of boundary terms.)
We have shown that equation (1) implies equation (2) as long as u is continuously differentiable. The key to the concept of weak solution is that there exist functions u which satisfy equation (2) for any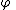
, and such u may not be differentiable and thus, they do not satisfy equation (1). A simple example of such function is u(t, x) = |t − x| for all t and x. (That u defined in this way satisfies equation (2) is easy enough to check, one needs to integrate separately on the regions above and below the line x = t and use integration by parts.) A solution u of equation (2) is called a weak solution of equation (1).
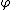, such that whatever derivatives in u show up in the equation, they are "transferred" via integration by parts to 
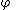. In this way one obtains solutions to the original equation which are not necessarily differentiable.
The approach illustrated above works for equations more general than the wave equation. Indeed, consider a linear differential operator
in an open set
W in Rn
where the multi-index (α1, α2, ..., αn) varies over some finite set in Nn and the coefficients
are smooth enough functions of x.
The differential equation P(x, ∂)u(x) = 0 can, after being multiplied by a smooth test function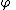
with compact support in W and integrated by parts, be written as
where the differential operator Q(x, ∂) is given by the formula
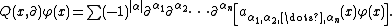
The number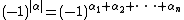
shows up because one needs α1 + α2 + ... + αn integrations by parts to transfer all the partial derivatives from u to
in each term of the differential equation, and each integration by parts entails a multiplication by −1.
The differential operator Q(x, ∂) is the formal adjoint of P(x, ∂) (see also adjoint of an operator for the concept of adjoint).
In summary, if the original (strong) problem was to find a |α|-times differentiable function u defined on the open set W such that
(a so-called strong solution), then an integrable function u would be said to be a weak solution if
for every smooth function
with compact support in W.
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a weak solution (also called a generalized solution) to an ordinary
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
or partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for different classes of equations. One of the most important is based on the notion of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
.
Avoiding the language of distributions, one starts with a differential equation and rewrites it in such a way that no derivatives of the solution of the equation show up (the new form is called the weak formulation
Weak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
, and the solutions to it are called weak solutions). Somewhat surprisingly, a differential equation may have solutions which are not differentiable; and the weak formulation allows one to find such solutions.
Weak solutions are important because a great many differential equations encountered in modelling real world phenomena do not admit sufficiently smooth solutions and then the only way of solving such equations is using the weak formulation. Even in situations where an equation does have differentiable solutions, it is often convenient to first prove the existence of weak solutions and only later show that those solutions are in fact smooth enough.
A concrete example
As an illustration of the concept, consider the first-order wave equationWave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
(see partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
for the notation) where u = u(t, x) is a function of two real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variables. Assume that u is continuously differentiable on the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R2, multiply this equation (1) by a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
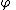of compact support, and integrate. One obtains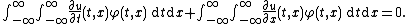Using Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
which allows one to interchange the order of integration, as well as integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
(in t for the first term and in x for the second term) this equation becomes
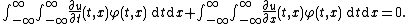
(Notice that while the integrals go from −∞ to ∞, the integrals are essentially over a finite box because
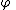has compact support, and it is this observation which also allows for integration by parts without the introduction of boundary terms.)We have shown that equation (1) implies equation (2) as long as u is continuously differentiable. The key to the concept of weak solution is that there exist functions u which satisfy equation (2) for any
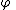, and such u may not be differentiable and thus, they do not satisfy equation (1). A simple example of such function is u(t, x) = |t − x| for all t and x. (That u defined in this way satisfies equation (2) is easy enough to check, one needs to integrate separately on the regions above and below the line x = t and use integration by parts.) A solution u of equation (2) is called a weak solution of equation (1).General case
The general idea which follows from this example is that, when solving a differential equation in u, one can rewrite it using a so-called test function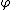, such that whatever derivatives in u show up in the equation, they are "transferred" via integration by parts to 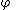. In this way one obtains solutions to the original equation which are not necessarily differentiable.The approach illustrated above works for equations more general than the wave equation. Indeed, consider a linear differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
in an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
W in Rn
where the multi-index (α1, α2, ..., αn) varies over some finite set in Nn and the coefficients
are smooth enough functions of x.The differential equation P(x, ∂)u(x) = 0 can, after being multiplied by a smooth test function
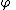with compact support in W and integrated by parts, be written aswhere the differential operator Q(x, ∂) is given by the formula
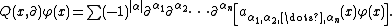
The number
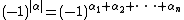
shows up because one needs α1 + α2 + ... + αn integrations by parts to transfer all the partial derivatives from u to
in each term of the differential equation, and each integration by parts entails a multiplication by −1.The differential operator Q(x, ∂) is the formal adjoint of P(x, ∂) (see also adjoint of an operator for the concept of adjoint).
In summary, if the original (strong) problem was to find a |α|-times differentiable function u defined on the open set W such that
(a so-called strong solution), then an integrable function u would be said to be a weak solution if
for every smooth function
with compact support in W.Other kinds of weak solution
The notion of weak solution based on distributions is sometimes inadequate. In the case of hyperbolic systems, the notion of weak solution based on distributions does not guarantee uniqueness, and it is necessary to supplement it with entropy conditions or some other selection criterion. In fully nonlinear PDE such as the Hamilton-Jacobi equation, there is a very different definition of weak solution called viscosity solutionViscosity solution
In mathematics, the viscosity solution concept was introduced in the early 1980s by Pierre-Louis Lions and Michael Crandall as a generalization of the classical concept of what is meant by a 'solution' to a partial differential equation...
.
Reference
- L.C. Evans, Partial Differential Equations, American Mathematical Society, Providence, 1998. ISBN 0-8218-0772-2