
Viscosity solution
Encyclopedia
In mathematics
, the viscosity solution concept was introduced in the early 1980s by Pierre-Louis Lions
and Michael Crandall as a generalization of the classical concept of what is meant by a 'solution' to a partial differential equation
(PDE). It has been found that the viscosity solution is the natural solution concept to use in many applications of PDE's, including for example first order equations arising in optimal control
(the Hamilton-Jacobi equation), differential game
s (the Isaacs equation) or front evolution problems, as well as second-order equations such as the ones arising in stochastic optimal control or stochastic differential games.
The classical concept was that a PDE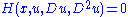
over a domain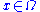 has a solution if we can find a function
has a solution if we can find a function
u(x) continuous and differentiable over the entire domain such that ,
,  ,
,  ,
, 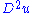 satisfy the above equation at every point.
satisfy the above equation at every point.
If a scalar equation is degenerate elliptic (defined below), one can define a type of weak solution
called viscosity solution.
Under the viscosity solution concept, u need not be everywhere differentiable. There may be points where either or
or 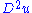 does not exist and yet u satisfies the equation in an appropriate sense. The definition allows only for certain kind of singularities, so that existence, uniqueness, and stability under uniform limits, hold for a large class of equations.
does not exist and yet u satisfies the equation in an appropriate sense. The definition allows only for certain kind of singularities, so that existence, uniqueness, and stability under uniform limits, hold for a large class of equations.
An equation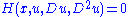 in a domain
in a domain  is defined to be degenerate elliptic if for any two symmetric matrices
is defined to be degenerate elliptic if for any two symmetric matrices 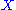 and
and  such that
such that  is positive definite
is positive definite
, and any values of ,
,  and
and 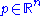 , we have the inequality
, we have the inequality 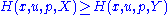 . For example
. For example 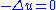 is degenerate elliptic. Any first order equation is degenerate elliptic.
is degenerate elliptic. Any first order equation is degenerate elliptic.
An upper semicontinuous function in
in  is defined to be a subsolution of a degenerate elliptic equation in the viscosity sense if for any point
is defined to be a subsolution of a degenerate elliptic equation in the viscosity sense if for any point 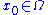 and any
and any  function
function  such that
such that  and
and  in a neighborhood of
in a neighborhood of 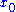 , we have
, we have 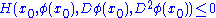 .
.
An lower semicontinuous function in
in  is defined to be a supersolution of a degenerate elliptic equation in the viscosity sense if for any point
is defined to be a supersolution of a degenerate elliptic equation in the viscosity sense if for any point 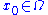 and any
and any 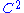 function
function 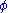 such that
such that  and
and  in a neighborhood of
in a neighborhood of  , we have
, we have 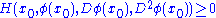 .
.
A continuous
function u is a viscosity solution of the PDE if it is both a viscosity supersolution and a viscosity subsolution.
in 1983 regarding the Hamilton-Jacobi equation. The name is justified by the fact that the existence of solutions was obtained by the vanishing viscosity method. The definition of solution had actually been given earlier by Lawrence Evans in 1980. Subsequently the definition and properties of viscosity solutions for the Hamilton-Jacobi equation were refined in a joint work by Crandall, Evans and Lions in 1984.
For a few years the work on viscosity solutions concentrated on first order equations because it was not known whether second order elliptic equations would have a unique viscosity solution except in very particular cases. The breakthrough result came with the method introduced by Robert Jensen in 1988 to prove the comparison principle using a regularization of the graph of the solution through parallel surfaces (replaced by sup-convolutions in more modern proofs).
In subsequent years the concept of viscosity solution has become increasingly prevalent in analysis of degenerate elliptic PDE. Based on their stability properties, Barles and Souganidis obtained a very simple and general proof of convergence of finite difference schemes. Further regularity properties of viscosity solutions were obtained, especially in the uniformly elliptic case with the work of Luis Caffarelli
. Viscosity solutions have become a central concept in the study of elliptic PDE as can be corroborated by the fact that currently the Users guide has more than 800 citations, being the most cited paper of mathematics for six years straight from 2003 to 2008 according to mathscinet
.
In the modern approach, the existence of solutions is obtained most often though the Perron method. The vanishing viscosity method is not practical for second order equations in general since the addition of artificial viscosity does not guarantee the existence of a classical solution. Moreover, the definition of viscosity solutions does not involve any viscosity of any kind. Thus, it has been suggested that the name viscosity solution does not represent the concept appropriately. Yet, the name persists because of the history of the subject. Other names that were suggested were Crandall-Lions solutions, in honor to their pioneers,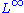 -weak solutions, referring to their stability properties, or comparison solutions, referring to their most characteristic property.
-weak solutions, referring to their stability properties, or comparison solutions, referring to their most characteristic property.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the viscosity solution concept was introduced in the early 1980s by Pierre-Louis Lions
Pierre-Louis Lions
Pierre-Louis Lions is a French mathematician. His parents were Jacques-Louis Lions, a mathematician and at that time professor at the University of Nancy, who in particular became President of the International Mathematical Union, and Andrée Olivier, his wife...
and Michael Crandall as a generalization of the classical concept of what is meant by a 'solution' to a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
(PDE). It has been found that the viscosity solution is the natural solution concept to use in many applications of PDE's, including for example first order equations arising in optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
(the Hamilton-Jacobi equation), differential game
Differential game
In game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. The problem usually consists of two actors, a pursuer and an evader, with conflicting goals...
s (the Isaacs equation) or front evolution problems, as well as second-order equations such as the ones arising in stochastic optimal control or stochastic differential games.
The classical concept was that a PDE
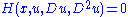
over a domain
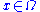 has a solution if we can find a function
has a solution if we can find a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
u(x) continuous and differentiable over the entire domain such that
 ,
,  ,
,  ,
, 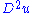 satisfy the above equation at every point.
satisfy the above equation at every point.If a scalar equation is degenerate elliptic (defined below), one can define a type of weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
called viscosity solution.
Under the viscosity solution concept, u need not be everywhere differentiable. There may be points where either
 or
or 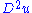 does not exist and yet u satisfies the equation in an appropriate sense. The definition allows only for certain kind of singularities, so that existence, uniqueness, and stability under uniform limits, hold for a large class of equations.
does not exist and yet u satisfies the equation in an appropriate sense. The definition allows only for certain kind of singularities, so that existence, uniqueness, and stability under uniform limits, hold for a large class of equations.Definition
There are several equivalent ways to phrase the definition of viscosity solutions. See for example the section II.4 of Fleming and Soner's book or the definition using semi-jets in the Users Guide.An equation
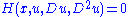 in a domain
in a domain  is defined to be degenerate elliptic if for any two symmetric matrices
is defined to be degenerate elliptic if for any two symmetric matrices 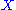 and
and  such that
such that  is positive definite
is positive definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, and any values of
 ,
,  and
and 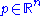 , we have the inequality
, we have the inequality 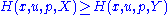 . For example
. For example 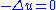 is degenerate elliptic. Any first order equation is degenerate elliptic.
is degenerate elliptic. Any first order equation is degenerate elliptic.An upper semicontinuous function
 in
in  is defined to be a subsolution of a degenerate elliptic equation in the viscosity sense if for any point
is defined to be a subsolution of a degenerate elliptic equation in the viscosity sense if for any point 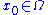 and any
and any  function
function  such that
such that  and
and  in a neighborhood of
in a neighborhood of 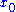 , we have
, we have 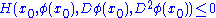 .
.An lower semicontinuous function
 in
in  is defined to be a supersolution of a degenerate elliptic equation in the viscosity sense if for any point
is defined to be a supersolution of a degenerate elliptic equation in the viscosity sense if for any point 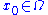 and any
and any 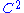 function
function 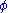 such that
such that  and
and  in a neighborhood of
in a neighborhood of  , we have
, we have  .
.A continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
function u is a viscosity solution of the PDE if it is both a viscosity supersolution and a viscosity subsolution.
Basic properties
The three basic properties of viscosity solutions are existence, uniqueness and stability.- The uniqueness of solutions requires some extra structural assumptions on the equation. Yet it can be shown for a very large class of degenerate elliptic equations. It is a direct consequence of the comparison principle. Some simple examples where comparison principle holds are
-
 with H uniformly continuous in x.
with H uniformly continuous in x. - (Uniformly elliptic case)
 so that
so that  is Lipschitz with respect to all variableas and for every
is Lipschitz with respect to all variableas and for every  and
and  ,
,  for some
for some  .
.
- The existence of solutions holds in all cases where the comparison principle holds and the boundary conditions can be enforced in some way (through barrier functionBarrier functionIn constrained optimization, a field of mathematics, a barrier function is a continuous function whose value on a point increases to infinity as the point approaches the boundary of the feasible region . It is used as a penalizing term for violations of constraints...
s in the case of a Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
). For first order equations, it can be obtained using the vanishing viscosity method or for most equations using Perron's method. - The stability of solutions in
 holds as follows: a locally uniform limit of a sequence of solutions (or subsolutions, or supersolutions) is a solution (or subsolution, or supersolution).
holds as follows: a locally uniform limit of a sequence of solutions (or subsolutions, or supersolutions) is a solution (or subsolution, or supersolution).
- The existence of solutions holds in all cases where the comparison principle holds and the boundary conditions can be enforced in some way (through barrier function
History
The term viscosity solutions first appear in the work of Michael Crandall and Pierre-Louis LionsPierre-Louis Lions
Pierre-Louis Lions is a French mathematician. His parents were Jacques-Louis Lions, a mathematician and at that time professor at the University of Nancy, who in particular became President of the International Mathematical Union, and Andrée Olivier, his wife...
in 1983 regarding the Hamilton-Jacobi equation. The name is justified by the fact that the existence of solutions was obtained by the vanishing viscosity method. The definition of solution had actually been given earlier by Lawrence Evans in 1980. Subsequently the definition and properties of viscosity solutions for the Hamilton-Jacobi equation were refined in a joint work by Crandall, Evans and Lions in 1984.
For a few years the work on viscosity solutions concentrated on first order equations because it was not known whether second order elliptic equations would have a unique viscosity solution except in very particular cases. The breakthrough result came with the method introduced by Robert Jensen in 1988 to prove the comparison principle using a regularization of the graph of the solution through parallel surfaces (replaced by sup-convolutions in more modern proofs).
In subsequent years the concept of viscosity solution has become increasingly prevalent in analysis of degenerate elliptic PDE. Based on their stability properties, Barles and Souganidis obtained a very simple and general proof of convergence of finite difference schemes. Further regularity properties of viscosity solutions were obtained, especially in the uniformly elliptic case with the work of Luis Caffarelli
Luis Caffarelli
Luis A. Caffarelli is an Argentinian mathematician and leader in the field of partial differential equations and their applications....
. Viscosity solutions have become a central concept in the study of elliptic PDE as can be corroborated by the fact that currently the Users guide has more than 800 citations, being the most cited paper of mathematics for six years straight from 2003 to 2008 according to mathscinet
Mathematical Reviews
Mathematical Reviews is a journal and online database published by the American Mathematical Society that contains brief synopses of many articles in mathematics, statistics and theoretical computer science.- Reviews :...
.
In the modern approach, the existence of solutions is obtained most often though the Perron method. The vanishing viscosity method is not practical for second order equations in general since the addition of artificial viscosity does not guarantee the existence of a classical solution. Moreover, the definition of viscosity solutions does not involve any viscosity of any kind. Thus, it has been suggested that the name viscosity solution does not represent the concept appropriately. Yet, the name persists because of the history of the subject. Other names that were suggested were Crandall-Lions solutions, in honor to their pioneers,
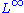 -weak solutions, referring to their stability properties, or comparison solutions, referring to their most characteristic property.
-weak solutions, referring to their stability properties, or comparison solutions, referring to their most characteristic property.

