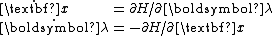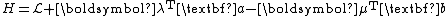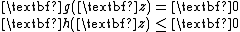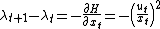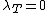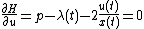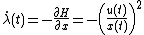Optimal control
Encyclopedia
Optimal control theory, an extension of the calculus of variations
, is a mathematical optimization
method for deriving control policies
. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman
in the United States.
(a sufficient condition).
We begin with a simple example. Consider a car traveling on a straight line through a hilly road. The question is, how should the driver press the accelerator pedal in order to minimize the total traveling time? Clearly in this example, the term control law refers specifically to the way in which the driver presses the accelerator and shifts the gears. The "system" consists of both the car and the road, and the optimality criterion is the minimization of the total traveling time. Control problems usually include ancillary constraint
s. For example the amount of available fuel might be limited, the accelerator pedal cannot be pushed through the floor of the car, speed limits, etc.
A proper cost functional is a mathematical expression giving the traveling time as a function of the speed, geometrical considerations, and initial conditions of the system. It is often the case that the constraints are interchangeable with the cost functional.
Another optimal control problem is to find the way to drive the car so as to minimize its fuel consumption, given that it must complete a given course in a time not exceeding some amount. Yet another control problem is to minimize the total monetary cost of completing the trip, given assumed monetary prices for time and fuel.
A more abstract framework goes as follows. Minimize the continuous-time cost functional

subject to the first-order dynamic constraints
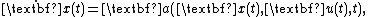
the algebraic path constraints

and the boundary conditions

where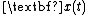 is the state,
is the state,  is the control,
is the control,  is the independent variable (generally speaking, time),
is the independent variable (generally speaking, time),  is the initial time, and
is the initial time, and  is the terminal time. The terms
is the terminal time. The terms 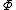 and
and  are called the endpoint cost and Lagrangian
are called the endpoint cost and Lagrangian
, respectively. Furthermore, it is noted that the path constraints are in general inequality constraints and thus may not be active (i.e., equal to zero) at the optimal solution. It is also noted that the optimal control problem as stated above may have multiple solutions (i.e., the solution may not be unique). Thus, it is most often the case that any solution to the optimal control problem is locally minimizing.
to the optimal control problem is locally minimizing.
. The LQ problem is stated as follows. Minimize the quadratic continuous-time cost functional
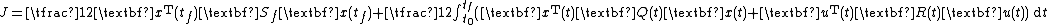
Subject to the linear first-order dynamic constraints

and the initial condition

A particular form of the LQ problem that arises in many control system problems is that of the linear quadratic regulator (LQR) where all of the matrices (i.e., ,
, 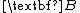 ,
,  , and
, and 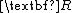 ) are constant, the initial time is arbitrarily set to zero, and the terminal time is taken in the limit
) are constant, the initial time is arbitrarily set to zero, and the terminal time is taken in the limit  (this last assumption is what is known as infinite horizon). The LQR problem is stated as follows. Minimize the infinite horizon quadratic continuous-time cost functional
(this last assumption is what is known as infinite horizon). The LQR problem is stated as follows. Minimize the infinite horizon quadratic continuous-time cost functional
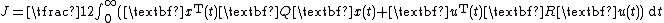
Subject to the linear time-invariant first-order dynamic constraints
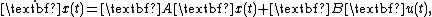
and the initial condition
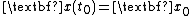
In the finite-horizon case the matrices are restricted in that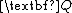 and
and  are positive semi-definite and positive definite, respectively. In the infinite-horizon case, however, the matrices
are positive semi-definite and positive definite, respectively. In the infinite-horizon case, however, the matrices
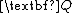 and
and 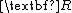 are not only positive-semidefinite and positive-definite, respectively, but are also constant. These additional restrictions on
are not only positive-semidefinite and positive-definite, respectively, but are also constant. These additional restrictions on
 and
and  in the infinite-horizon case are enforced to ensure that the cost functional remains positive. Furthermore, in order to ensure that the cost function is bounded, the additional restriction is imposed that the pair
in the infinite-horizon case are enforced to ensure that the cost functional remains positive. Furthermore, in order to ensure that the cost function is bounded, the additional restriction is imposed that the pair 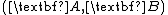 is controllable. Note that the LQ or LQR cost functional can be thought of physically as attempting to minimize the control energy (measured as a quadratic form).
is controllable. Note that the LQ or LQR cost functional can be thought of physically as attempting to minimize the control energy (measured as a quadratic form).
The infinite horizon problem (i.e., LQR) may seem overly restrictive and essentially useless because it assumes that the operator is driving the system to zero-state and hence driving the output of the system to zero. This is indeed correct. However the problem of driving the output to a desired nonzero level can be solved after the zero output one is. In fact, it can be proved that this secondary LQR problem can be solved in a very straightforward manner. It has been shown in classical optimal control theory that the LQ (or LQR) optimal control has the feedback form
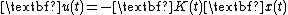
where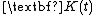 is a properly dimensioned matrix, given as
is a properly dimensioned matrix, given as

and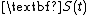 is the solution of the differential Riccati equation
is the solution of the differential Riccati equation
. The differential Riccati equation is given as

For the finite horizon LQ problem, the Riccati equation is integrated backward in time using the terminal boundary condition
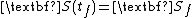
For the infinite horizon LQR problem, the differential Riccati equation is replaced with the algebraic Riccati equation (ARE) given as

Understanding that the ARE arises from infinite horizon problem, the matrices ,
,  ,
, 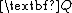 , and
, and 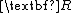 are all constant. It is noted that there are in general two solutions to the algebraic Riccati equation and the positive definite (or positive semi-definite) solution is the one that is used to compute the feedback gain. It is noted that the LQ (LQR) problem was elegantly solved by Rudolf Kalman
are all constant. It is noted that there are in general two solutions to the algebraic Riccati equation and the positive definite (or positive semi-definite) solution is the one that is used to compute the feedback gain. It is noted that the LQ (LQR) problem was elegantly solved by Rudolf Kalman
.
. Thus, the resulting dynamical system is a Hamiltonian system
of the form
where
is the augmented Hamiltonian and in an indirect method, the boundary-value problem is solved (using the appropriate boundary or transversality conditions). The beauty of using an indirect method is that the state and adjoint (i.e.,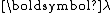 ) are solved for and the resulting solution is readily verified to be an extremal trajectory. The disadvantage of indirect methods is that the boundary-value problem is often extremely difficult to solve (particularly for problems that span large time intervals or problems with interior point constraints). A well-known software program that implements indirect methods is BNDSCO.
) are solved for and the resulting solution is readily verified to be an extremal trajectory. The disadvantage of indirect methods is that the boundary-value problem is often extremely difficult to solve (particularly for problems that span large time intervals or problems with interior point constraints). A well-known software program that implements indirect methods is BNDSCO.
The approach that has risen to prominence in numerical optimal control over the past two decades (i.e., from the 1980s to the present) is that of so called direct methods. In a direct method, the state and/or control are approximated using an appropriate function approximation (e.g., polynomial approximation or piecewise constant parameterization). Simultaneously, the cost functional is approximated as a cost function. Then, the coefficients of the function approximations are treated as optimization variables and the problem is "transcribed" to a nonlinear optimization problem of the form:
Minimize
subject to the algebraic constraints
Depending upon the type of direct method employed, the size of the nonlinear optimization problem can be quite small (e.g., as in a direct shooting or quasilinearization method) or may be quite large (e.g., a direct collocation method). In the latter case (i.e., a collocation method), the nonlinear optimization problem may be literally thousands to tens of thousands of variables and constraints. Given the size of many NLPs arising from a direct method, it may appear somewhat counter-intuitive that solving the nonlinear optimization problem is easier than solving the boundary-value problem. It is, however, the fact that the NLP is easier to solve than the boundary-value problem. The reason for the relative ease of computation, particularly of a direct collocation method, is that the NLP is sparse and many well-known software programs exist (e.g., SNOPT
) to solve large sparse NLPs. As a result, the range of problems that can be solved via direct methods (particularly direct collocation methods which are very popular these days) is significantly larger than the range of problems that can be solved via indirect methods. In fact, direct methods have become so popular these days that many people have written elaborate software programs that employ these methods. In particular, many such programs written in FORTRAN include DIRCOL, SOCS, OTIS, GESOP/ASTOS
and DITAN. In recent years, due to the advent of the MATLAB programming language, optimal control software in MATLAB has become more common. Examples of academically developed MATLAB software tools implementing direct methods include RIOTS,DIDO
, DIRECT, and GPOPS, while an example of an industry developed MATLAB tool is PROPT
. These software tools have increased significantly the opportunity for people to explore complex optimal control problems both for academic research and industrial-strength problems. Finally, it is noted that general-purpose MATLAB
optimization environments such as TOMLAB
have made coding complex optimal control problems significantly easier than was previously possible in languages such as C and FORTRAN
.
ly, contemporary control theory is now primarily concerned with discrete time
systems and solutions. The Theory of Consistent Approximations provides conditions under which solutions to a series of increasingly accurate discretized optimal control problem converge to the solution of the original, continuous-time problem. Not all discretization methods have this property, even seemingly obvious ones. For instance, using a variable step-size routine to integrate the problem's dynamic equations may generate a gradient which does not converge to zero (or point in the right direction) as the solution is approached. The direct method RIOTS is based on the Theory of Consistent Approximation.
) . The costate summarizes in one number the marginal value of expanding or contracting the state variable next turn. The marginal value is not only the gains accruing to it next turn but associated with the duration of the program. It is nice when
. The costate summarizes in one number the marginal value of expanding or contracting the state variable next turn. The marginal value is not only the gains accruing to it next turn but associated with the duration of the program. It is nice when  can be solved analytically, but usually the most one can do is describe it sufficiently well that the intuition can grasp the character of the solution and an equation solver can solve numerically for the values.
can be solved analytically, but usually the most one can do is describe it sufficiently well that the intuition can grasp the character of the solution and an equation solver can solve numerically for the values.
Having obtained , the turn-t optimal value for the control can usually be solved as a differential equation conditional on knowledge of
, the turn-t optimal value for the control can usually be solved as a differential equation conditional on knowledge of  . Again it is infrequent, especially in continuous-time problems, that one obtains the value of the control or the state explicitly. Usually the strategy is to solve for thresholds and regions that characterize the optimal control and use a numerical solver to isolate the actual choice values in time.
. Again it is infrequent, especially in continuous-time problems, that one obtains the value of the control or the state explicitly. Usually the strategy is to solve for thresholds and regions that characterize the optimal control and use a numerical solver to isolate the actual choice values in time.
 to date
to date 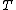 . At date
. At date  there is
there is  ore in the ground, and the instantaneous stock of ore
ore in the ground, and the instantaneous stock of ore 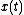 declines at the rate the mine owner extracts it u(t). The mine owner extracts ore at cost
declines at the rate the mine owner extracts it u(t). The mine owner extracts ore at cost 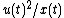 and sells ore at a constant price
and sells ore at a constant price  . He does not value the ore remaining in the ground at time
. He does not value the ore remaining in the ground at time  (there is no "scrap value"). He chooses the rate of extraction in time u(t) to maximize profits over the period of ownership with no time discounting.
(there is no "scrap value"). He chooses the rate of extraction in time u(t) to maximize profits over the period of ownership with no time discounting.
Journals
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, is a mathematical optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
method for deriving control policies
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman
Richard Bellman
Richard Ernest Bellman was an American applied mathematician, celebrated for his invention of dynamic programming in 1953, and important contributions in other fields of mathematics.-Biography:...
in the United States.
General method
Optimal control deals with the problem of finding a control law for a given system such that a certain optimality criterion is achieved. A control problem includes a cost functional that is a function of state and control variables. An optimal control is a set of differential equations describing the paths of the control variables that minimize the cost functional. The optimal control can be derived using Pontryagin's maximum principle (a necessary condition also known as Pontryagin's minimum principle or simply Pontryagin's Principle), or by solving the Hamilton-Jacobi-Bellman equationHamilton-Jacobi-Bellman equation
The Hamilton–Jacobi–Bellman equation is a partial differential equation which is central to optimal control theory. The solution of the HJB equation is the 'value function', which gives the optimal cost-to-go for a given dynamical system with an associated cost function.When solved locally, the...
(a sufficient condition).
We begin with a simple example. Consider a car traveling on a straight line through a hilly road. The question is, how should the driver press the accelerator pedal in order to minimize the total traveling time? Clearly in this example, the term control law refers specifically to the way in which the driver presses the accelerator and shifts the gears. The "system" consists of both the car and the road, and the optimality criterion is the minimization of the total traveling time. Control problems usually include ancillary constraint
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
s. For example the amount of available fuel might be limited, the accelerator pedal cannot be pushed through the floor of the car, speed limits, etc.
A proper cost functional is a mathematical expression giving the traveling time as a function of the speed, geometrical considerations, and initial conditions of the system. It is often the case that the constraints are interchangeable with the cost functional.
Another optimal control problem is to find the way to drive the car so as to minimize its fuel consumption, given that it must complete a given course in a time not exceeding some amount. Yet another control problem is to minimize the total monetary cost of completing the trip, given assumed monetary prices for time and fuel.
A more abstract framework goes as follows. Minimize the continuous-time cost functional

subject to the first-order dynamic constraints
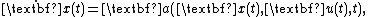
the algebraic path constraints

and the boundary conditions

where
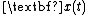 is the state,
is the state,  is the control,
is the control,  is the independent variable (generally speaking, time),
is the independent variable (generally speaking, time),  is the initial time, and
is the initial time, and  is the terminal time. The terms
is the terminal time. The terms 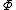 and
and  are called the endpoint cost and Lagrangian
are called the endpoint cost and LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
, respectively. Furthermore, it is noted that the path constraints are in general inequality constraints and thus may not be active (i.e., equal to zero) at the optimal solution. It is also noted that the optimal control problem as stated above may have multiple solutions (i.e., the solution may not be unique). Thus, it is most often the case that any solution
 to the optimal control problem is locally minimizing.
to the optimal control problem is locally minimizing.Linear quadratic control
A special case of the general nonlinear optimal control problem given in the previous section is the linear quadratic (LQ) optimal control problemLinear-quadratic regulator
The theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic functional is called the LQ problem...
. The LQ problem is stated as follows. Minimize the quadratic continuous-time cost functional
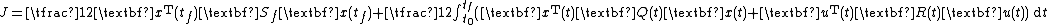
Subject to the linear first-order dynamic constraints

and the initial condition

A particular form of the LQ problem that arises in many control system problems is that of the linear quadratic regulator (LQR) where all of the matrices (i.e.,
 ,
, 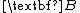 ,
,  , and
, and 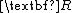 ) are constant, the initial time is arbitrarily set to zero, and the terminal time is taken in the limit
) are constant, the initial time is arbitrarily set to zero, and the terminal time is taken in the limit  (this last assumption is what is known as infinite horizon). The LQR problem is stated as follows. Minimize the infinite horizon quadratic continuous-time cost functional
(this last assumption is what is known as infinite horizon). The LQR problem is stated as follows. Minimize the infinite horizon quadratic continuous-time cost functional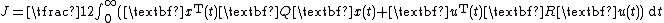
Subject to the linear time-invariant first-order dynamic constraints
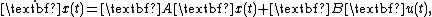
and the initial condition
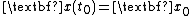
In the finite-horizon case the matrices are restricted in that
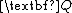 and
and  are positive semi-definite and positive definite, respectively. In the infinite-horizon case, however, the matrices
are positive semi-definite and positive definite, respectively. In the infinite-horizon case, however, the matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
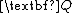 and
and 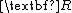 are not only positive-semidefinite and positive-definite, respectively, but are also constant. These additional restrictions on
are not only positive-semidefinite and positive-definite, respectively, but are also constant. These additional restrictions on and
and  in the infinite-horizon case are enforced to ensure that the cost functional remains positive. Furthermore, in order to ensure that the cost function is bounded, the additional restriction is imposed that the pair
in the infinite-horizon case are enforced to ensure that the cost functional remains positive. Furthermore, in order to ensure that the cost function is bounded, the additional restriction is imposed that the pair 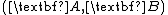 is controllable. Note that the LQ or LQR cost functional can be thought of physically as attempting to minimize the control energy (measured as a quadratic form).
is controllable. Note that the LQ or LQR cost functional can be thought of physically as attempting to minimize the control energy (measured as a quadratic form).The infinite horizon problem (i.e., LQR) may seem overly restrictive and essentially useless because it assumes that the operator is driving the system to zero-state and hence driving the output of the system to zero. This is indeed correct. However the problem of driving the output to a desired nonzero level can be solved after the zero output one is. In fact, it can be proved that this secondary LQR problem can be solved in a very straightforward manner. It has been shown in classical optimal control theory that the LQ (or LQR) optimal control has the feedback form
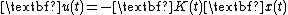
where
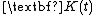 is a properly dimensioned matrix, given as
is a properly dimensioned matrix, given as
and
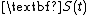 is the solution of the differential Riccati equation
is the solution of the differential Riccati equationRiccati equation
In mathematics, a Riccati equation is any ordinary differential equation that is quadratic in the unknown function. In other words, it is an equation of the form y' = q_0 + q_1 \, y + q_2 \, y^2...
. The differential Riccati equation is given as

For the finite horizon LQ problem, the Riccati equation is integrated backward in time using the terminal boundary condition
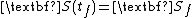
For the infinite horizon LQR problem, the differential Riccati equation is replaced with the algebraic Riccati equation (ARE) given as

Understanding that the ARE arises from infinite horizon problem, the matrices
 ,
,  ,
, 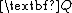 , and
, and 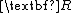 are all constant. It is noted that there are in general two solutions to the algebraic Riccati equation and the positive definite (or positive semi-definite) solution is the one that is used to compute the feedback gain. It is noted that the LQ (LQR) problem was elegantly solved by Rudolf Kalman
are all constant. It is noted that there are in general two solutions to the algebraic Riccati equation and the positive definite (or positive semi-definite) solution is the one that is used to compute the feedback gain. It is noted that the LQ (LQR) problem was elegantly solved by Rudolf KalmanRudolf Kalman
Rudolf Emil Kálmán is a Hungarian-American electrical engineer, mathematical system theorist, and college professor, who was educated in the United States, and has done most of his work there. He is currently a retired professor from three different institutes of technology and universities...
.
Numerical methods for optimal control
Optimal control problems are generally nonlinear and therefore, generally do not have analytic solutions (e.g., like the linear-quadratic optimal control problem). As a result, it is necessary to employ numerical methods to solve optimal control problems. In the early years of optimal control (circa 1950s to 1980s) the favored approach for solving optimal control problems was that of indirect methods. In an indirect method, the calculus of variations is employed to obtain the first-order optimality conditions. These conditions result in a two-point (or, in the case of a complex problem, a multi-point) boundary-value problem. This boundary-value problem actually has a special structure because it arises from taking the derivative of a HamiltonianHamiltonian (control theory)
The Hamiltonian of optimal control theory was developed by L. S. Pontryagin as part of his minimum principle. It was inspired by, but is distinct from, the Hamiltonian of classical mechanics. Pontryagin proved that a necessary condition for solving the optimal control problem is that the control...
. Thus, the resulting dynamical system is a Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
of the form
where
is the augmented Hamiltonian and in an indirect method, the boundary-value problem is solved (using the appropriate boundary or transversality conditions). The beauty of using an indirect method is that the state and adjoint (i.e.,
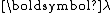 ) are solved for and the resulting solution is readily verified to be an extremal trajectory. The disadvantage of indirect methods is that the boundary-value problem is often extremely difficult to solve (particularly for problems that span large time intervals or problems with interior point constraints). A well-known software program that implements indirect methods is BNDSCO.
) are solved for and the resulting solution is readily verified to be an extremal trajectory. The disadvantage of indirect methods is that the boundary-value problem is often extremely difficult to solve (particularly for problems that span large time intervals or problems with interior point constraints). A well-known software program that implements indirect methods is BNDSCO.The approach that has risen to prominence in numerical optimal control over the past two decades (i.e., from the 1980s to the present) is that of so called direct methods. In a direct method, the state and/or control are approximated using an appropriate function approximation (e.g., polynomial approximation or piecewise constant parameterization). Simultaneously, the cost functional is approximated as a cost function. Then, the coefficients of the function approximations are treated as optimization variables and the problem is "transcribed" to a nonlinear optimization problem of the form:
Minimize
subject to the algebraic constraints
Depending upon the type of direct method employed, the size of the nonlinear optimization problem can be quite small (e.g., as in a direct shooting or quasilinearization method) or may be quite large (e.g., a direct collocation method). In the latter case (i.e., a collocation method), the nonlinear optimization problem may be literally thousands to tens of thousands of variables and constraints. Given the size of many NLPs arising from a direct method, it may appear somewhat counter-intuitive that solving the nonlinear optimization problem is easier than solving the boundary-value problem. It is, however, the fact that the NLP is easier to solve than the boundary-value problem. The reason for the relative ease of computation, particularly of a direct collocation method, is that the NLP is sparse and many well-known software programs exist (e.g., SNOPT
SNOPT
SNOPT is a software package for solving large-scale optimization problems written by Philip Gill, Walter Murray and Michael Saunders....
) to solve large sparse NLPs. As a result, the range of problems that can be solved via direct methods (particularly direct collocation methods which are very popular these days) is significantly larger than the range of problems that can be solved via indirect methods. In fact, direct methods have become so popular these days that many people have written elaborate software programs that employ these methods. In particular, many such programs written in FORTRAN include DIRCOL, SOCS, OTIS, GESOP/ASTOS
Astos
ASTOS is a Trajectory optimization and simulation tool for launch and re-entry missions, orbit transfers, design optimization and for re-entry safety assessments. It solves Aerospace problems with a data driven interface and automatic initial guesses...
and DITAN. In recent years, due to the advent of the MATLAB programming language, optimal control software in MATLAB has become more common. Examples of academically developed MATLAB software tools implementing direct methods include RIOTS,DIDO
DIDO (optimal control)
DIDO is a MATLAB program for solving hybrid optimal control problems. Powered by the pseudospectral knotting method, the general-purpose program is named after Dido, the legendary founder and first queen of Carthage who is famous in mathematics for her remarkable solution to a constrained optimal...
, DIRECT, and GPOPS, while an example of an industry developed MATLAB tool is PROPT
PROPT
The PROPT MATLAB Optimal Control Software is a new generation platform for solving applied optimal control and parameters estimation problems.The platform was developed by MATLAB Programming Contest Winner, in 2008...
. These software tools have increased significantly the opportunity for people to explore complex optimal control problems both for academic research and industrial-strength problems. Finally, it is noted that general-purpose MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
optimization environments such as TOMLAB
TOMLAB
The TOMLAB Optimization Environment is a modeling platform for solving applied optimization problems in MATLAB.-Description:TOMLAB is a general purpose development and modeling environment in MATLAB for research, teaching and practical solution of optimization problems...
have made coding complex optimal control problems significantly easier than was previously possible in languages such as C and FORTRAN
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
.
Discrete-time optimal control
The examples thus far have shown continuous time systems and control solutions. In fact, as optimal control solutions are now often implemented digitalDigital
A digital system is a data technology that uses discrete values. By contrast, non-digital systems use a continuous range of values to represent information...
ly, contemporary control theory is now primarily concerned with discrete time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
systems and solutions. The Theory of Consistent Approximations provides conditions under which solutions to a series of increasingly accurate discretized optimal control problem converge to the solution of the original, continuous-time problem. Not all discretization methods have this property, even seemingly obvious ones. For instance, using a variable step-size routine to integrate the problem's dynamic equations may generate a gradient which does not converge to zero (or point in the right direction) as the solution is approached. The direct method RIOTS is based on the Theory of Consistent Approximation.
Examples
A common solution strategy in many optimal control problems is to solve for the costate (sometimes called the shadow priceShadow price
In constrained optimization in economics, the shadow price is the instantaneous change per unit of the constraint in the objective value of the optimal solution of an optimization problem obtained by relaxing the constraint...
)
 . The costate summarizes in one number the marginal value of expanding or contracting the state variable next turn. The marginal value is not only the gains accruing to it next turn but associated with the duration of the program. It is nice when
. The costate summarizes in one number the marginal value of expanding or contracting the state variable next turn. The marginal value is not only the gains accruing to it next turn but associated with the duration of the program. It is nice when  can be solved analytically, but usually the most one can do is describe it sufficiently well that the intuition can grasp the character of the solution and an equation solver can solve numerically for the values.
can be solved analytically, but usually the most one can do is describe it sufficiently well that the intuition can grasp the character of the solution and an equation solver can solve numerically for the values.Having obtained
 , the turn-t optimal value for the control can usually be solved as a differential equation conditional on knowledge of
, the turn-t optimal value for the control can usually be solved as a differential equation conditional on knowledge of  . Again it is infrequent, especially in continuous-time problems, that one obtains the value of the control or the state explicitly. Usually the strategy is to solve for thresholds and regions that characterize the optimal control and use a numerical solver to isolate the actual choice values in time.
. Again it is infrequent, especially in continuous-time problems, that one obtains the value of the control or the state explicitly. Usually the strategy is to solve for thresholds and regions that characterize the optimal control and use a numerical solver to isolate the actual choice values in time.Finite time
Consider the problem of a mine owner who must decide at what rate to extract ore from his mine. He owns rights to the ore from date to date
to date 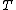 . At date
. At date  there is
there is  ore in the ground, and the instantaneous stock of ore
ore in the ground, and the instantaneous stock of ore 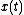 declines at the rate the mine owner extracts it u(t). The mine owner extracts ore at cost
declines at the rate the mine owner extracts it u(t). The mine owner extracts ore at cost 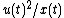 and sells ore at a constant price
and sells ore at a constant price  . He does not value the ore remaining in the ground at time
. He does not value the ore remaining in the ground at time  (there is no "scrap value"). He chooses the rate of extraction in time u(t) to maximize profits over the period of ownership with no time discounting.
(there is no "scrap value"). He chooses the rate of extraction in time u(t) to maximize profits over the period of ownership with no time discounting.| 1. Discrete-time version The manager maximizes profit 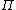 : : subject to the law of evolution for the state variable 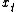 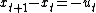 Form the Hamiltonian and differentiate: 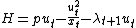
As the mine owner does not value the ore remaining at time 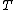 , ,
Using the above equations, it is easy to solve for the 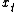 and and 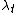 series series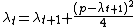 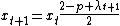 and using the initial and turn-T conditions, the 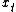 series can be solved explicitly, giving series can be solved explicitly, giving 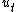 . . |
2. Continuous-time version The manager maximizes profit  : :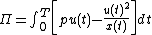 subject to the law of evolution for the state variable  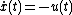 Form the Hamiltonian and differentiate: 
As the mine owner does not value the ore remaining at time 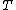 , ,
Using the above equations, it is easy to solve for the differential equations governing  and and  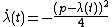 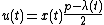 and using the initial and turn-T conditions, the functions can be solved numerically. |
See also
- Dynamic programmingDynamic programmingIn mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
- Bellman equationBellman equationA Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
- Linear-quadratic regulatorLinear-quadratic regulatorThe theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic functional is called the LQ problem...
- Stochastic controlStochastic controlStochastic control is a subfield of control theory which deals with the existence of uncertainty in the data. The designer assumes, in a Bayesian probability-driven fashion, that a random noise with known probability distribution affects the state evolution and the observation of the controllers...
- Trajectory optimizationTrajectory optimizationTrajectory optimization is the process of designing a trajectory that minimizes or maximizes some measure of performance within prescribed constraint boundaries...
- Gauss pseudospectral methodGauss pseudospectral methodThe Gauss pseudospectral method , one of many topics named after Carl Friedrich Gauss, is a direct transcription method for discretizing a continuous optimal control problem into a nonlinear program . The Gauss pseudospectral method differs from several other pseudospectral methods in that the...
- Pseudospectral optimal controlPseudospectral optimal controlPseudospectral optimal control is a computational method for solving optimal control problems. Pseudospectral optimal control techniques have been extensively used to solve a wide range of problems such as those arising in UAV trajectory generation, missile guidance, control of robotic arms,...
- Pursuit-evasionPursuit-evasionPursuit-evasion is a family of problems in mathematics and computer science in which one group attempts to track down members of another group in an environment. Early work on problems of this type modeled the environment geometrically...
games - DIDODIDO (optimal control)DIDO is a MATLAB program for solving hybrid optimal control problems. Powered by the pseudospectral knotting method, the general-purpose program is named after Dido, the legendary founder and first queen of Carthage who is famous in mathematics for her remarkable solution to a constrained optimal...
- JModelica.orgJModelica.orgJModelica.org is a free and open source platform based on the Modelica modeling language for modeling, simulation, optimization and analysis of complex dynamic systems. The platform is maintained and developed by Modelon AB in collaboration with academic and industrial institutions, notably Lund...
(Modelica-based open source platform for dynamic optimization) - PROPT (Optimal Control Software for MATLAB)PROPTThe PROPT MATLAB Optimal Control Software is a new generation platform for solving applied optimal control and parameters estimation problems.The platform was developed by MATLAB Programming Contest Winner, in 2008...
- SNOPTSNOPTSNOPT is a software package for solving large-scale optimization problems written by Philip Gill, Walter Murray and Michael Saunders....
- Sliding mode controlSliding mode controlIn control theory, sliding mode control, or SMC, is a nonlinear control method that alters the dynamics of a nonlinear system by application of a discontinuous control signal that forces the system to "slide" along a cross-section of the system's normal behavior. The state-feedback control law is...
- DNSS pointDNSS pointDNSS points arise in optimal control problems that exhibit multiple optimal solutions. A DNSS point-named alphabetically after Deckert and Nishimura, Sethi, and Skiba-is an indifference point in an optimal control problem such that starting from such a point, the problem has more than one different...
- Brachistochrone
Further reading
Books- Athans, M. A. and Falb, P. L., Optimal Control, McGraw-Hill, New York, 1966.
- Becerra, V.M., 2008, Optimal control. Scholarpedia, 3(1):5354
- Bryson, A. E., 1969. Applied Optimal Control: Optimization, Estimation, & Control.
- Evans, L.C., An Introduction to Optimal Control Theory (available free online)
- Ross, I. M. A Primer on Pontryagin's Principle in Optimal Control, Collegiate Publishers, 2009. ISBN 978-0-9843571-0-9. (http://www.ElissarGlobal.com free chapter available online)
- H. O. Fattorini and S. S. Sritharan, "Existence of Optimal Controls for Viscous Flow Problems," Proceedings of the Royal Society of London Series A, Vol. 439, 1992, pp. 81–102.
- H. O. Fattorini and S. S. Sritharan, "Necessary and Sufficient Conditions for Optimal Controls in Viscous Flow," Proceedings of the Royal Society of Edinburgh, Series A, Vol. 124A, 1994, pp. 211–251.
- H. O. Fattorini and S. S. Sritharan, "Optimal chattering controls for viscous flow," Nonlinear analysis, Theory, Methods and Applications, Vol. 25, No. 8, pp. 763–797, 1995.
- H. O. Fattorini and S. S. Sritharan,"Optimal control problems with state constraints in fluid mechanics and combustion," Applied Mathematics and Optimization, Vol. 38(2), 1998, pp. 159–192.
- Kirk, D. E., 2004. Optimal Control Theory: An Introduction.
- Lebedev, L. P., and Cloud, M. J., 2003. The Calculus of Variations and Functional Analysis with Optimal Control and Applications in Mechanics. World Scientific. Especially chpt. 2.
- Lewis, F. L., and Syrmos, V. L., 19nn. Optimal Control, 2nd ed. John Wiley & Sons.
- S. S. Sritharan, "Optimal Control of Viscous Flow", SIAM, 1998. (http://www.ec-securehost.com/SIAM/ot59.html)
- S. S. Sritharan, "An Optimal Control Problem in Exterior Hydrodynamics," Proceedings of the Royal Society of Edinburgh, Series 121A, 1992, pp. 5–32.
- S. S. Sritharan,"Deterministic and stochastic control of viscous flow with linear, monotone and hyper viscosities," Applied Mathematics and Optimization, Vol. 41(2), pp. 255–308, 2000.
- Stengel, R. F., 1994. Optimal Control and Estimation. Dover.
- Sethi, S. P., and Thompson, G. L., 2000. Optimal Control Theory: Applications to Management Science and Economics, 2nd edition, Springer (ISBN 0387280928 and ISBN 0792386086). Slides are available at http://www.utdallas.edu/~sethi/OPRE7320presentation.html
- Sontag, Eduardo D. Mathematical Control Theory: Deterministic Finite Dimensional Systems. Second Edition. Springer. (ISBN 0-387-984895) (available free online)
- Brogan, William L. 1990. Modern Control Theory. ISBN 0135897637
Journals
- Optimal Control Applications and Methods. John Wiley & Sons, Inc.
- SIAM Journal of Control and Optimization.
External links
- ACADO Toolkit - Open Source Toolkit for Automatic Control and Dynamic Optimization (C++, MATLAB interface available)
- Dr. Benoît CHACHUAT: Automatic Control Laboratory - Nonlinear Programming, Calculus of Variations and Optimal Control.
- Flood: An open source neural networks C++ library
- GPOPS - Open Source Pseudospectral Optimal Control Solver in MATLAB
- Elmer G. Wiens: Optimal Control - Applications of Optimal Control Theory Using the Pontryagin Maximum Principle with interactive models.
- PPOPT - MATLAB Optimal Control Software
- PSOPT - Open Source Pseudospectral Optimal Control Solver in C++
- GESOP - Graphical Environment for Simulation and OPtimization