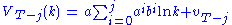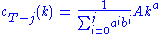
Dynamic programming
Encyclopedia
In mathematics
and computer science
, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblem
s which are only slightly smaller and optimal substructure
(described below). When applicable, the method takes far less time than naive methods.
The key idea behind dynamic programming is quite simple. In general, to solve a given problem, we need to solve different parts of the problem (subproblems), then combine the solutions of the subproblems to reach an overall solution. Often, many of these subproblems are really the same. The dynamic programming approach seeks to solve each subproblem only once, thus reducing the number of computations. This is especially useful when the number of repeating subproblems is exponentially large.
Top-down dynamic programming simply means storing the results of certain calculations, which are later used again since the completed calculation is a sub-problem of a larger calculation. Bottom-up dynamic programming involves formulating a complex calculation as a recursive
series of simpler calculations.
to describe the process of solving problems where one needs to find the best decisions one after another. By 1953, he refined this to the modern meaning, referring specifically to nesting smaller decision problems inside larger decisions, and the field was thereafter recognized by the IEEE as a systems analysis
and engineering
topic. Bellman's contribution is remembered in the name of the Bellman equation
, a central result of dynamic programming which restates an optimization problem in recursive
form.
The word dynamic was chosen by Bellman to capture the time-varying aspect of the problems, and also because it sounded impressive. The word programming referred to the use of the method to find an optimal program, in the sense of a military schedule for training or logistics. This usage is the same as that in the phrases linear programming
and mathematical programming, a synonym for mathematical optimization.
Dynamic programming is both a mathematical optimization method and a computer programming method. In both contexts it refers to simplifying a complicated problem by breaking it down into simpler subproblems in a recursive
manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively; Bellman called this the "Principle of Optimality". Likewise, in computer science, a problem that can be broken down recursively is said to have optimal substructure
.
If subproblems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the subproblems. In the optimization literature this relationship is called the Bellman equation
.
of the system at times i from 1 to n. The definition of Vn(y) is the value obtained in state y at the last time n. The values Vi at earlier times i=n-1,n-2,...,2,1 can be found by working backwards, using a recursive
relationship called the Bellman equation
. For i=2,...n, Vi -1 at any state y is calculated from Vi by maximizing a simple function (usually the sum) of the gain from decision i-1 and the function Vi at the new state of the system if this decision is made. Since Vi has already been calculated for the needed states, the above operation yields Vi -1 for those states. Finally, V1 at the initial state of the system is the value of the optimal solution. The optimal values of the decision variables can be recovered, one by one, by tracking back the calculations already performed.
and overlapping subproblem
s. However, when the overlapping problems are much smaller than the original problem, the strategy is called "divide and conquer
" rather than "dynamic programming". This is why mergesort, quicksort, and finding all matches of a regular expression
are not classified as dynamic programming problems.
Optimal substructure means that the solution to a given optimization problem can be obtained by the combination of optimal solutions to its subproblems. Consequently, the first step towards devising a dynamic programming solution is to check whether the problem exhibits such optimal substructure. Such optimal substructures are usually described by means of recursion
. For example, given a graph G=(V,E), the shortest path p from a vertex u to a vertex v exhibits optimal substructure: take any intermediate vertex w on this shortest path p. If p is truly the shortest path, then the path p1 from u to w and p2 from w to v are indeed the shortest paths between the corresponding vertices (by the simple cut-and-paste argument described in CLRS). Hence, one can easily formulate the solution for finding shortest paths in a recursive manner, which is what the Bellman-Ford algorithm
does.
Overlapping subproblems means that the space of subproblems must be small, that is, any recursive algorithm solving the problem should solve the same subproblems over and over, rather than generating new subproblems. For example, consider the recursive formulation for generating the Fibonacci series: Fi = Fi-1 + Fi-2, with base case F1=F2=1. Then F43 = F42 + F41, and F42 = F41 + F40. Now F41 is being solved in the recursive subtrees of both F43 as well as F42. Even though the total number of subproblems is actually small (only 43 of them), we end up solving the same problems over and over if we adopt a naive recursive solution such as this. Dynamic programming takes account of this fact and solves each subproblem only once. Note that the subproblems must be only slightly smaller (typically taken to mean a constant additive factor) than the larger problem; when they are a multiplicative factor smaller the problem is no longer classified as dynamic programming.
This can be achieved in either of two ways:
Some programming language
s can automatically memoize
the result of a function call with a particular set of arguments, in order to speed up call-by-name evaluation (this mechanism is referred to as call-by-need). Some languages make it possible portably (e.g. Scheme, Common Lisp
or Perl
), some need special extensions (e.g. C++
, see). Some languages have automatic memoization
built in, such as tabled Prolog
and J
, which supports memoization with the M. adverb . In any case, this is only possible for a referentially transparent function.
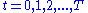and must decide how much to consume and how much to save in each period.
Let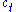
be consumption in period 
, and assume consumption yields utility
as long as the consumer lives. Assume the consumer is impatient, so that he discounts future utility by a factor 
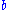each period, where 
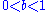. Let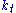 
be capital
in period
. Assume initial capital is a given amount 
, and suppose that this period's capital and consumption determine next period's capital as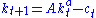 
, where 
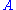is a positive constant and 
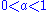. Assume capital cannot be negative. Then the consumer's decision problem can be written as follows:
Written this way, the problem looks complicated, because it involves solving for all the choice variables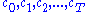
and 
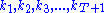simultaneously. (Note that 
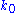is not a choice variable—the consumer's initial capital is taken as given.)
The dynamic programming approach to solving this problem involves breaking it apart into a sequence of smaller decisions. To do so, we define a sequence of value functions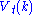
, for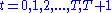 
which represent the value of having any amount of capital 
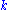at each time 
. Note that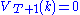 
, that is, there is (by assumption) no utility from having capital after death.
The value of any quantity of capital at any previous time can be calculated by backward induction
using the Bellman equation
. In this problem, for each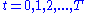
, the Bellman equation is
This problem is much simpler than the one we wrote down before, because it involves only two decision variables,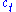
and 
. Intuitively, instead of choosing his whole lifetime plan at birth, the consumer can take things one step at a time. At time 
, his current capital 
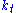is given, and he only needs to choose current consumption 
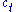and saving 
.
To actually solve this problem, we work backwards. For simplicity, the current level of capital is denoted as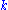
. 
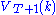is already known, so using the Bellman equation once we can calculate 
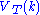, and so on until we get to 
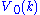, which is the value of the initial decision problem for the whole lifetime. In other words, once we know 
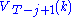, we can calculate 
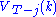, which is the maximum of 
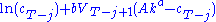, where 
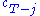is the choice variable and 
.
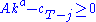Working backwards, it can be shown that the value function at time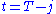
is
where each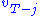
is a constant, and the optimal amount to consume at time 
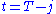is
which can be simplified to
We see that it is optimal to consume a larger fraction of current wealth as one gets older, finally consuming all remaining wealth in period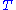
, the last period of life.
for the shortest path problem
is a successive approximation scheme that solves the dynamic programming functional equation for the shortest path problem by the Reaching method.
In fact, Dijkstra's explanation of the logic behind the algorithm, namely
is a paraphrasing of Bellman's
famous Principle of Optimality in the context of the shortest path problem
.
function fib(n)
if n = 0 return 0
if n = 1 return 1
return fib(n − 1) + fib(n − 2)
Notice that if we call, say,
In particular,
Now, suppose we have a simple map
object, m, which maps each value of
var m := map(0 → 0, 1 → 1)
function fib(n)
if map m does not contain key n
m[n] := fib(n − 1) + fib(n − 2)
return m[n]
This technique of saving values that have already been calculated is called memoization
; this is the top-down approach, since we first break the problem into subproblems and then calculate and store values.
In the bottom-up approach we calculate the smaller values of
function fib(n)
var previousFib := 0, currentFib := 1
if n = 0
return 0
else repeat n − 1 times //loop is skipped if n=1
var newFib := previousFib + currentFib
previousFib := currentFib
currentFib := newFib
return currentFib
In both these examples, we only calculate
. For example, when , four possible solutions are
There are at least three possible approaches: brute force
, backtracking
, and dynamic programming.
Brute force consists of checking all assignments of zeros and ones and counting those that have balanced rows and columns (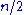
zeros and 
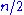ones). As there are 
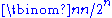possible assignments, this strategy is not practical except maybe up to 
.
Backtracking for this problem consists of choosing some order of the matrix elements and recursively placing ones or zeros, while checking that in every row and column the number of elements that have not been assigned plus the number of ones or zeros are both at least n / 2. While more sophisticated than brute force, this approach will visit every solution once, making it impractical for n larger than six, since the number of solutions is already 116963796250 for n = 8, as we shall see.
Dynamic programming makes it possible to count the number of solutions without visiting them all. Imagine backtracking values for the first row - what information would we require about the remaining rows, in order to be able to accurately count the solutions obtained for each first row values? We consider boards, where , whose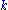
rows contain 
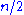zeros and 
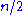ones. The function f to which memoization
is applied maps vectors of n pairs of integers to the number of admissible boards (solutions). There is one pair for each column and its two components indicate respectively the number of ones and zeros that have yet to be placed in that column. We seek the value of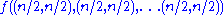
(
arguments or one vector of 
elements). The process of subproblem creation involves iterating over every one of 
possible assignments for the top row of the board, and going through every column, subtracting one from the appropriate element of the pair for that column, depending on whether the assignment for the top row contained a zero or a one at that position. If any one of the results is negative, then the assignment is invalid and does not contribute to the set of solutions (recursion stops). Otherwise, we have an assignment for the top row of the board and recursively compute the number of solutions to the remaining board, adding the numbers of solutions for every admissible assignment of the top row and returning the sum, which is being memoized. The base case is the trivial subproblem, which occurs for a board. The number of solutions for this board is either zero or one, depending on whether the vector is a permutation of 
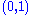and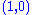 
pairs or not.
For example, in the two boards shown above the sequences of vectors would be
The number of solutions is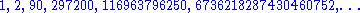
Links to the MAPLE implementation of the dynamic programming approach may be found among the external links.
with n × n squares and a cost-function c(i, j) which returns a cost associated with square i, j (i being the row, j being the column). For instance (on a 5 × 5 checkerboard),
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblem
Overlapping subproblem
In computer science, a problem is said to have overlapping subproblems if the problem can be broken down into subproblems which are reused several times or a recursive algorithm for the problem solves the same subproblem over and over rather than always generating new subproblem.For example, the...
s which are only slightly smaller and optimal substructure
Optimal substructure
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions to its subproblems...
(described below). When applicable, the method takes far less time than naive methods.
The key idea behind dynamic programming is quite simple. In general, to solve a given problem, we need to solve different parts of the problem (subproblems), then combine the solutions of the subproblems to reach an overall solution. Often, many of these subproblems are really the same. The dynamic programming approach seeks to solve each subproblem only once, thus reducing the number of computations. This is especially useful when the number of repeating subproblems is exponentially large.
Top-down dynamic programming simply means storing the results of certain calculations, which are later used again since the completed calculation is a sub-problem of a larger calculation. Bottom-up dynamic programming involves formulating a complex calculation as a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
series of simpler calculations.
History
The term dynamic programming was originally used in the 1940s by Richard BellmanRichard Bellman
Richard Ernest Bellman was an American applied mathematician, celebrated for his invention of dynamic programming in 1953, and important contributions in other fields of mathematics.-Biography:...
to describe the process of solving problems where one needs to find the best decisions one after another. By 1953, he refined this to the modern meaning, referring specifically to nesting smaller decision problems inside larger decisions, and the field was thereafter recognized by the IEEE as a systems analysis
Systems analysis
Systems analysis is the study of sets of interacting entities, including computer systems analysis. This field is closely related to requirements analysis or operations research...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
topic. Bellman's contribution is remembered in the name of the Bellman equation
Bellman equation
A Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
, a central result of dynamic programming which restates an optimization problem in recursive
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
form.
The word dynamic was chosen by Bellman to capture the time-varying aspect of the problems, and also because it sounded impressive. The word programming referred to the use of the method to find an optimal program, in the sense of a military schedule for training or logistics. This usage is the same as that in the phrases linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
and mathematical programming, a synonym for mathematical optimization.
Overview
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively; Bellman called this the "Principle of Optimality". Likewise, in computer science, a problem that can be broken down recursively is said to have optimal substructure
Optimal substructure
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions to its subproblems...
.
If subproblems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the subproblems. In the optimization literature this relationship is called the Bellman equation
Bellman equation
A Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
.
Dynamic programming in mathematical optimization
In terms of mathematical optimization, dynamic programming usually refers to simplifying a decision by breaking it down into a sequence of decision steps over time. This is done by defining a sequence of value functions V1, V2, ... Vn, with an argument y representing the stateState variable
A state variable is one of the set of variables that describe the "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour...
of the system at times i from 1 to n. The definition of Vn(y) is the value obtained in state y at the last time n. The values Vi at earlier times i=n-1,n-2,...,2,1 can be found by working backwards, using a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
relationship called the Bellman equation
Bellman equation
A Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
. For i=2,...n, Vi -1 at any state y is calculated from Vi by maximizing a simple function (usually the sum) of the gain from decision i-1 and the function Vi at the new state of the system if this decision is made. Since Vi has already been calculated for the needed states, the above operation yields Vi -1 for those states. Finally, V1 at the initial state of the system is the value of the optimal solution. The optimal values of the decision variables can be recovered, one by one, by tracking back the calculations already performed.
Dynamic programming in computer programming
There are two key attributes that a problem must have in order for dynamic programming to be applicable: optimal substructureOptimal substructure
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions to its subproblems...
and overlapping subproblem
Overlapping subproblem
In computer science, a problem is said to have overlapping subproblems if the problem can be broken down into subproblems which are reused several times or a recursive algorithm for the problem solves the same subproblem over and over rather than always generating new subproblem.For example, the...
s. However, when the overlapping problems are much smaller than the original problem, the strategy is called "divide and conquer
Divide and conquer algorithm
In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
" rather than "dynamic programming". This is why mergesort, quicksort, and finding all matches of a regular expression
Regular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
are not classified as dynamic programming problems.
Optimal substructure means that the solution to a given optimization problem can be obtained by the combination of optimal solutions to its subproblems. Consequently, the first step towards devising a dynamic programming solution is to check whether the problem exhibits such optimal substructure. Such optimal substructures are usually described by means of recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. For example, given a graph G=(V,E), the shortest path p from a vertex u to a vertex v exhibits optimal substructure: take any intermediate vertex w on this shortest path p. If p is truly the shortest path, then the path p1 from u to w and p2 from w to v are indeed the shortest paths between the corresponding vertices (by the simple cut-and-paste argument described in CLRS). Hence, one can easily formulate the solution for finding shortest paths in a recursive manner, which is what the Bellman-Ford algorithm
Bellman-Ford algorithm
The Bellman–Ford algorithm computes single-source shortest paths in a weighted digraph.For graphs with only non-negative edge weights, the faster Dijkstra's algorithm also solves the problem....
does.
Overlapping subproblems means that the space of subproblems must be small, that is, any recursive algorithm solving the problem should solve the same subproblems over and over, rather than generating new subproblems. For example, consider the recursive formulation for generating the Fibonacci series: Fi = Fi-1 + Fi-2, with base case F1=F2=1. Then F43 = F42 + F41, and F42 = F41 + F40. Now F41 is being solved in the recursive subtrees of both F43 as well as F42. Even though the total number of subproblems is actually small (only 43 of them), we end up solving the same problems over and over if we adopt a naive recursive solution such as this. Dynamic programming takes account of this fact and solves each subproblem only once. Note that the subproblems must be only slightly smaller (typically taken to mean a constant additive factor) than the larger problem; when they are a multiplicative factor smaller the problem is no longer classified as dynamic programming.
- Top-down approach: This is the direct fall-out of the recursive formulation of any problem. If the solution to any problem can be formulated recursively using the solution to its subproblems, and if its subproblems are overlapping, then one can easily memoizeMemoizationIn computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs...
or store the solutions to the subproblems in a table. Whenever we attempt to solve a new subproblem, we first check the table to see if it is already solved. If a solution has been recorded, we can use it directly, otherwise we solve the subproblem and add its solution to the table.
- Bottom-up approachTop-down and bottom-up designTop–down and bottom–up are strategies of information processing and knowledge ordering, mostly involving software, but also other humanistic and scientific theories . In practice, they can be seen as a style of thinking and teaching...
: This is the more interesting case. Once we formulate the solution to a problem recursively as in terms of its subproblems, we can try reformulating the problem in a bottom-up fashion: try solving the subproblems first and use their solutions to build-on and arrive at solutions to bigger subproblems. This is also usually done in a tabular form by iteratively generating solutions to bigger and bigger subproblems by using the solutions to small subproblems. For example, if we already know the values of F41 and F40, we can directly calculate the value of F42.
Some programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s can automatically memoize
Memoization
In computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs...
the result of a function call with a particular set of arguments, in order to speed up call-by-name evaluation (this mechanism is referred to as call-by-need). Some languages make it possible portably (e.g. Scheme, Common Lisp
Common Lisp
Common Lisp, commonly abbreviated CL, is a dialect of the Lisp programming language, published in ANSI standard document ANSI INCITS 226-1994 , . From the ANSI Common Lisp standard the Common Lisp HyperSpec has been derived for use with web browsers...
or Perl
Perl
Perl is a high-level, general-purpose, interpreted, dynamic programming language. Perl was originally developed by Larry Wall in 1987 as a general-purpose Unix scripting language to make report processing easier. Since then, it has undergone many changes and revisions and become widely popular...
), some need special extensions (e.g. C++
C++
C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
, see). Some languages have automatic memoization
Memoization
In computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs...
built in, such as tabled Prolog
Prolog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
and J
J (programming language)
The J programming language, developed in the early 1990s by Kenneth E. Iverson and Roger Hui, is a synthesis of APL and the FP and FL function-level languages created by John Backus....
, which supports memoization with the M. adverb . In any case, this is only possible for a referentially transparent function.
Optimal consumption and saving
A mathematical optimization problem that is often used in teaching dynamic programming to economists (because it can be solved by hand) concerns a consumer who lives over the periods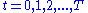 and must decide how much to consume and how much to save in each period.Let
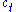be consumption in period , and assume consumption yields utilityUtility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
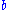as long as the consumer lives. Assume the consumer is impatient, so that he discounts future utility by a factor each period, where 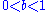. Let 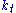be capitalCapital (economics)
In economics, capital, capital goods, or real capital refers to already-produced durable goods used in production of goods or services. The capital goods are not significantly consumed, though they may depreciate in the production process...
in period
. Assume initial capital is a given amount , and suppose that this period's capital and consumption determine next period's capital as 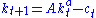, where 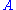is a positive constant and 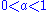. Assume capital cannot be negative. Then the consumer's decision problem can be written as follows:-
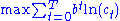subject to 
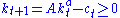for all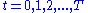 
Written this way, the problem looks complicated, because it involves solving for all the choice variables
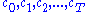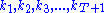and simultaneously. (Note that 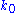is not a choice variable—the consumer's initial capital is taken as given.)The dynamic programming approach to solving this problem involves breaking it apart into a sequence of smaller decisions. To do so, we define a sequence of value functions
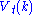, for 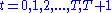which represent the value of having any amount of capital 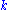at each time . Note that 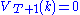, that is, there is (by assumption) no utility from having capital after death.The value of any quantity of capital at any previous time can be calculated by backward induction
Backward induction
Backward induction is the process of reasoning backwards in time, from the end of a problem or situation, to determine a sequence of optimal actions. It proceeds by first considering the last time a decision might be made and choosing what to do in any situation at that time. Using this...
using the Bellman equation
Bellman equation
A Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
. In this problem, for each
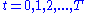, the Bellman equation is-
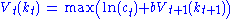subject to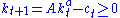 
This problem is much simpler than the one we wrote down before, because it involves only two decision variables,
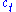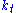and . Intuitively, instead of choosing his whole lifetime plan at birth, the consumer can take things one step at a time. At time , his current capital is given, and he only needs to choose current consumption 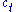and saving .To actually solve this problem, we work backwards. For simplicity, the current level of capital is denoted as
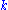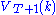. is already known, so using the Bellman equation once we can calculate 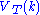, and so on until we get to 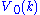, which is the value of the initial decision problem for the whole lifetime. In other words, once we know 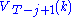, we can calculate 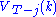, which is the maximum of 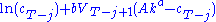, where 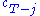is the choice variable and 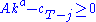.Working backwards, it can be shown that the value function at time
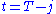is
where each
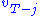is a constant, and the optimal amount to consume at time 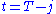is
which can be simplified to
-
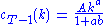, and 
, and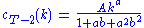 
, etc.
We see that it is optimal to consume a larger fraction of current wealth as one gets older, finally consuming all remaining wealth in period
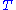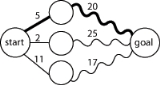
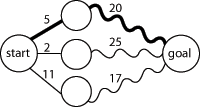
, the last period of life.Dijkstra's algorithm for the shortest path problem
From a dynamic programming point of view, Dijkstra's algorithmDijkstra's algorithm
Dijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree...
for the shortest path problem
Shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
is a successive approximation scheme that solves the dynamic programming functional equation for the shortest path problem by the Reaching method.
In fact, Dijkstra's explanation of the logic behind the algorithm, namely
is a paraphrasing of Bellman's
Richard Bellman
Richard Ernest Bellman was an American applied mathematician, celebrated for his invention of dynamic programming in 1953, and important contributions in other fields of mathematics.-Biography:...
famous Principle of Optimality in the context of the shortest path problem
Shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
.
Fibonacci sequence
Here is a naïve implementation of a function finding the nth member of the Fibonacci sequence, based directly on the mathematical definition:function fib(n)
if n = 0 return 0
if n = 1 return 1
return fib(n − 1) + fib(n − 2)
Notice that if we call, say,
fib(5), we produce a call tree that calls the function on the same value many different times:
-
fib(5) -
fib(4) + fib(3) -
(fib(3) + fib(2)) + (fib(2) + fib(1)) -
((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1)) -
(((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
In particular,
fib(2) was calculated three times from scratch. In larger examples, many more values of fib, or subproblems, are recalculated, leading to an exponential time algorithm.Now, suppose we have a simple map
Associative array
In computer science, an associative array is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection....
object, m, which maps each value of
fib that has already been calculated to its result, and we modify our function to use it and update it. The resulting function requires only O(n) time instead of exponential time:var m := map(0 → 0, 1 → 1)
function fib(n)
if map m does not contain key n
m[n] := fib(n − 1) + fib(n − 2)
return m[n]
This technique of saving values that have already been calculated is called memoization
Memoization
In computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs...
; this is the top-down approach, since we first break the problem into subproblems and then calculate and store values.
In the bottom-up approach we calculate the smaller values of
fib first, then build larger values from them. This method also uses O(n) time since it contains a loop that repeats n − 1 times, however it only takes constant (O(1)) space, in contrast to the top-down approach which requires O(n) space to store the map.function fib(n)
var previousFib := 0, currentFib := 1
if n = 0
return 0
else repeat n − 1 times //loop is skipped if n=1
var newFib := previousFib + currentFib
previousFib := currentFib
currentFib := newFib
return currentFib
In both these examples, we only calculate
fib(2) one time, and then use it to calculate both fib(4) and fib(3), instead of computing it every time either of them is evaluated. (Note the calculation of the Fibonacci sequence is used to demonstrate dynamic programming. An O(1) formula, known as Binet's formula, exists from which an arbitrary term can be calculated, which is more efficient than any dynamic programming technique.)A type of balanced 0-1 matrix
Consider the problem of assigning values, either zero or one, to the positions of an matrix, even, so that each row and each column contains exactly zeros and ones. We ask how many different assignments there are for a given. For example, when , four possible solutions areThere are at least three possible approaches: brute force
Brute-force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
, backtracking
Backtracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
, and dynamic programming.
Brute force consists of checking all assignments of zeros and ones and counting those that have balanced rows and columns (
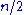zeros and 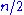ones). As there are 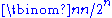possible assignments, this strategy is not practical except maybe up to .Backtracking for this problem consists of choosing some order of the matrix elements and recursively placing ones or zeros, while checking that in every row and column the number of elements that have not been assigned plus the number of ones or zeros are both at least n / 2. While more sophisticated than brute force, this approach will visit every solution once, making it impractical for n larger than six, since the number of solutions is already 116963796250 for n = 8, as we shall see.
Dynamic programming makes it possible to count the number of solutions without visiting them all. Imagine backtracking values for the first row - what information would we require about the remaining rows, in order to be able to accurately count the solutions obtained for each first row values? We consider boards, where , whose
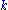rows contain 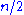zeros and 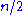ones. The function f to which memoizationMemoization
In computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs...
is applied maps vectors of n pairs of integers to the number of admissible boards (solutions). There is one pair for each column and its two components indicate respectively the number of ones and zeros that have yet to be placed in that column. We seek the value of
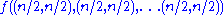( arguments or one vector of elements). The process of subproblem creation involves iterating over every one of possible assignments for the top row of the board, and going through every column, subtracting one from the appropriate element of the pair for that column, depending on whether the assignment for the top row contained a zero or a one at that position. If any one of the results is negative, then the assignment is invalid and does not contribute to the set of solutions (recursion stops). Otherwise, we have an assignment for the top row of the board and recursively compute the number of solutions to the remaining board, adding the numbers of solutions for every admissible assignment of the top row and returning the sum, which is being memoized. The base case is the trivial subproblem, which occurs for a board. 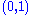The number of solutions for this board is either zero or one, depending on whether the vector is a permutation of and 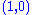pairs or not.For example, in the two boards shown above the sequences of vectors would be
((2, 2) (2, 2) (2, 2) (2, 2)) ((2, 2) (2, 2) (2, 2) (2, 2)) k = 4
0 1 0 1 0 0 1 1
((1, 2) (2, 1) (1, 2) (2, 1)) ((1, 2) (1, 2) (2, 1) (2, 1)) k = 3
1 0 1 0 0 0 1 1
((1, 1) (1, 1) (1, 1) (1, 1)) ((0, 2) (0, 2) (2, 0) (2, 0)) k = 2
0 1 0 1 1 1 0 0
((0, 1) (1, 0) (0, 1) (1, 0)) ((0, 1) (0, 1) (1, 0) (1, 0)) k = 1
1 0 1 0 1 1 0 0
((0, 0) (0, 0) (0, 0) (0, 0)) ((0, 0) (0, 0), (0, 0) (0, 0))
The number of solutions is
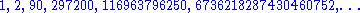
Links to the MAPLE implementation of the dynamic programming approach may be found among the external links.
Checkerboard
Consider a checkerboardCheckerboard
A checkerboard or chequerboard is a board of chequered pattern on which English draughts is played. It is an 8×8 board and the 64 squares are of alternating dark and light color, often red and black....
with n × n squares and a cost-function c(i, j) which returns a cost associated with square i, j (i being the row, j being the column). For instance (on a 5 × 5 checkerboard),
| 5 | 6 | 7 | 4 | 7 | 8 |
|---|---|---|---|---|---|
| 4 | 7 | 6 | 1 | 1 | 4 |
| 3 | 3 | 5 | 7 | 8 | 2 |
| 2 | - | 6 | 7 | 0 | - |
| 1 | - | - | *5* | - | - |
| |2 | |4 | ||||
| 5 | |||||
| 4 | |||||
| 3 | |||||
| 2 | x | x | x | ||
| 1 | o | ||||
| |2 | |4 | ||||
| 5 | |||||
| 4 | A | ||||
| 3 | B | C | D | ||
| 2 | |||||
| 1 | |||||
| |2 | |4 | if y = 2 |
