
Markov decision process
Encyclopedia
Markov decision processes (MDPs), named after Andrey Markov
, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problem
s solved via dynamic programming
and reinforcement learning
. MDPs were known at least as early as the 1950s (cf. Bellman 1957). Much research in the area was spawned due to Ronald A. Howard
's book, Dynamic Programming and Markov Processes, in 1960. Today they are used in a variety of areas, including robotics, automated control, economics and manufacturing.
More precisely, a Markov Decision Process is a discrete time
stochastic
control process. At each time step, the process is in some state , and the decision maker may choose any action
, and the decision maker may choose any action  that is available in state
that is available in state  . The process responds at the next time step by randomly moving into a new state
. The process responds at the next time step by randomly moving into a new state  , and giving the decision maker a corresponding reward
, and giving the decision maker a corresponding reward 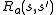 .
.
The probability that the process moves into its new state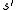 is influenced by the chosen action. Specifically, it is given by the state transition function
is influenced by the chosen action. Specifically, it is given by the state transition function  . Thus, the next state
. Thus, the next state 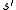 depends on the current state
depends on the current state  and the decision maker's action
and the decision maker's action  . But given
. But given  and
and  , it is conditionally independent of all previous states and actions; in other words, the state transitions of an MDP possess the Markov property
, it is conditionally independent of all previous states and actions; in other words, the state transitions of an MDP possess the Markov property
.
Markov decision processes are an extension of Markov chain
s; the difference is the addition of actions (allowing choice) and rewards (giving motivation). Conversely, if only one action exists for each state and all rewards are zero, a Markov decision process reduces to a Markov chain
.
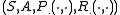 , where
, where
(The theory of Markov decision processes does not actually require or
or 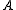 to be finite, but the basic algorithms below assume that they are finite.)
to be finite, but the basic algorithms below assume that they are finite.)
 that specifies the action
that specifies the action 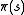 that the decision maker will choose when in state
that the decision maker will choose when in state  . Note that once a Markov decision process is combined with a policy in this way, this fixes the action for each state and the resulting combination behaves like a Markov chain
. Note that once a Markov decision process is combined with a policy in this way, this fixes the action for each state and the resulting combination behaves like a Markov chain
.
The goal is to choose a policy that will maximize some cumulative function of the random rewards, typically the expected discounted sum over a potentially infinite horizon:
that will maximize some cumulative function of the random rewards, typically the expected discounted sum over a potentially infinite horizon:
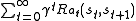 (where we choose
(where we choose 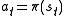 )
)
where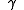 is the discount factor and satisfies
is the discount factor and satisfies 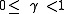 . (For example,
. (For example, 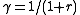 when the discount rate is r.)
when the discount rate is r.) 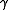 is typically close to 1.
is typically close to 1.
Because of the Markov property, the optimal policy for this particular problem can indeed be written as a function of only, as assumed above.
only, as assumed above.
or dynamic programming
. In what follows we present the latter approach.
Suppose we know the state transition function and the reward function
and the reward function 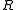 , and we wish to calculate the policy that maximizes the expected discounted reward.
, and we wish to calculate the policy that maximizes the expected discounted reward.
The standard family of algorithms to calculate this optimal policy requires storage for two arrays indexed by state: value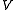 , which contains real values, and policy
, which contains real values, and policy  which contains actions. At the end of the algorithm,
which contains actions. At the end of the algorithm,  will contain the solution and
will contain the solution and 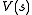 will contain the discounted sum of the rewards to be earned (on average) by following that solution from state
will contain the discounted sum of the rewards to be earned (on average) by following that solution from state  .
.
The algorithm has the following two kinds of steps, which are repeated in some order for all the states until no further changes take place.
They are
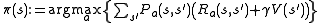
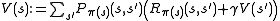
Their order depends on the variant of the algorithm; one can also do them for all states at once or state by state, and more often to some states than others. As long as no state is permanently excluded from either of the steps, the algorithm will eventually arrive at the correct solution.
,
the array is not used; instead, the value of
array is not used; instead, the value of 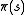 is calculated whenever it is needed. Shapley's 1953 paper on stochastic games included as a special case the value iteration method for MDPs, but this was recognized only later on.
is calculated whenever it is needed. Shapley's 1953 paper on stochastic games included as a special case the value iteration method for MDPs, but this was recognized only later on.
Substituting the calculation of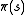 into the calculation of
into the calculation of  gives the combined step:
gives the combined step: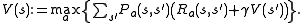
This update rule is iterated for all states until it converges with the left-hand side equal to the right-hand side (which is the Bellman equation
until it converges with the left-hand side equal to the right-hand side (which is the Bellman equation
for this problem).
Instead of repeating step two to convergence, it may be formulated and solved as a set of linear equations.
This variant has the advantage that there is a definite stopping condition: when the array does not change in the course of applying step 1 to all states, the algorithm is completed.
does not change in the course of applying step 1 to all states, the algorithm is completed.
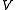 or
or  around those states recently) or based on use (those states are near the starting state, or otherwise of interest to the person or program using the algorithm).
around those states recently) or based on use (those states are near the starting state, or otherwise of interest to the person or program using the algorithm).
with only one player.
 is known when action is to be taken; otherwise
is known when action is to be taken; otherwise 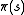 cannot be calculated. When this assumption is not true, the problem is called a partially observable Markov decision process or POMDP.
cannot be calculated. When this assumption is not true, the problem is called a partially observable Markov decision process or POMDP.
(Sutton and Barto, 1998).
For this purpose it is useful to define a further function, which corresponds to taking the action and then continuing optimally (or according to whatever policy one currently has):
and then continuing optimally (or according to whatever policy one currently has):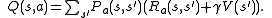
While this function is also unknown, experience during learning is based on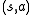 pairs (together with the outcome
pairs (together with the outcome 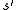 ); that is, "I was in state
); that is, "I was in state  and I tried doing
and I tried doing  and
and 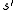 happened"). Thus, one has an array
happened"). Thus, one has an array 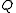 and uses experience to update it directly. This is known as Q-learning
and uses experience to update it directly. This is known as Q-learning
.
The power of reinforcement learning lies in its ability to solve the Markov decision process without computing the transition probabilities; note that transition probabilities are needed in value and policy iteration. Also, reinforcement learning can be combined with function approximation, and thereby one can solve problems with a very large number of states. Reinforcement Learning can also be handily performed within Monte Carlo simulators of systems.
If the state space and action space are finite,
If the state space and action space are continuous,
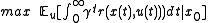
Where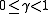
. Under this assumption, although the decision maker could make decision at any time, on the current state, he could not get more benefit to make more than one actions. It is better for him to take action only at the time when system transit from current state to another state. Under some conditions,(for detail check Corollary 3.14 of Continuous-Time Markov Decision Processes), if our optimal value function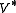 is independent of state i, we will have a following equation:
is independent of state i, we will have a following equation: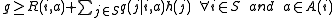
If there exists a function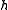 , then
, then  will be the smallest g could satisfied the above equation. In order to find the
will be the smallest g could satisfied the above equation. In order to find the 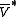 , we could have the following linear programming model:
, we could have the following linear programming model:
Andrey Markov
Andrey Andreyevich Markov was a Russian mathematician. He is best known for his work on theory of stochastic processes...
, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s solved via dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
and reinforcement learning
Reinforcement learning
Inspired by behaviorist psychology, reinforcement learning is an area of machine learning in computer science, concerned with how an agent ought to take actions in an environment so as to maximize some notion of cumulative reward...
. MDPs were known at least as early as the 1950s (cf. Bellman 1957). Much research in the area was spawned due to Ronald A. Howard
Ronald A. Howard
Ronald A. Howard has been a professor at Stanford University since 1965. In 1964 he defined the profession of decision analysis, and since then has been developing the field as professor in the Department of Engineering-Economic Systems in the School of Engineering at Stanford.Howard directs...
's book, Dynamic Programming and Markov Processes, in 1960. Today they are used in a variety of areas, including robotics, automated control, economics and manufacturing.
More precisely, a Markov Decision Process is a discrete time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
control process. At each time step, the process is in some state
 , and the decision maker may choose any action
, and the decision maker may choose any action  that is available in state
that is available in state  . The process responds at the next time step by randomly moving into a new state
. The process responds at the next time step by randomly moving into a new state  , and giving the decision maker a corresponding reward
, and giving the decision maker a corresponding reward 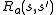 .
.The probability that the process moves into its new state
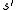 is influenced by the chosen action. Specifically, it is given by the state transition function
is influenced by the chosen action. Specifically, it is given by the state transition function  . Thus, the next state
. Thus, the next state 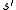 depends on the current state
depends on the current state  and the decision maker's action
and the decision maker's action  . But given
. But given  and
and  , it is conditionally independent of all previous states and actions; in other words, the state transitions of an MDP possess the Markov property
, it is conditionally independent of all previous states and actions; in other words, the state transitions of an MDP possess the Markov propertyMarkov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
.
Markov decision processes are an extension of Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s; the difference is the addition of actions (allowing choice) and rewards (giving motivation). Conversely, if only one action exists for each state and all rewards are zero, a Markov decision process reduces to a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
.
Definition
A Markov decision process is a 4-tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
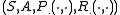 , where
, where-
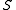 is a finite set of states,
is a finite set of states, -
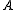 is a finite set of actions (alternatively,
is a finite set of actions (alternatively, 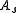 is the finite set of actions available from state
is the finite set of actions available from state  ),
), -
 is the probability that action
is the probability that action  in state
in state  at time
at time  will lead to state
will lead to state  at time
at time 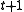 ,
, 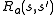 is the immediate reward (or expectedExpectedExpected may refer to:*Expectation*Expected value*Expected shortfall*Expected utility hypothesis*Expected return*Expected gainSee also*Unexpected...
is the immediate reward (or expectedExpectedExpected may refer to:*Expectation*Expected value*Expected shortfall*Expected utility hypothesis*Expected return*Expected gainSee also*Unexpected...
immediate reward) received after transition to state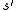 from state
from state  with transition probability
with transition probability 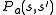 .
.
(The theory of Markov decision processes does not actually require
 or
or 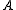 to be finite, but the basic algorithms below assume that they are finite.)
to be finite, but the basic algorithms below assume that they are finite.)Problem
The core problem of MDPs is to find a policy for the decision maker: a function that specifies the action
that specifies the action 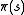 that the decision maker will choose when in state
that the decision maker will choose when in state  . Note that once a Markov decision process is combined with a policy in this way, this fixes the action for each state and the resulting combination behaves like a Markov chain
. Note that once a Markov decision process is combined with a policy in this way, this fixes the action for each state and the resulting combination behaves like a Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
.
The goal is to choose a policy
 that will maximize some cumulative function of the random rewards, typically the expected discounted sum over a potentially infinite horizon:
that will maximize some cumulative function of the random rewards, typically the expected discounted sum over a potentially infinite horizon: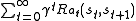 (where we choose
(where we choose 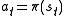 )
)where
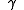 is the discount factor and satisfies
is the discount factor and satisfies 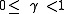 . (For example,
. (For example, 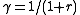 when the discount rate is r.)
when the discount rate is r.) 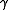 is typically close to 1.
is typically close to 1.Because of the Markov property, the optimal policy for this particular problem can indeed be written as a function of
 only, as assumed above.
only, as assumed above.Algorithms
MDPs can be solved by linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
or dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
. In what follows we present the latter approach.
Suppose we know the state transition function
 and the reward function
and the reward function 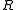 , and we wish to calculate the policy that maximizes the expected discounted reward.
, and we wish to calculate the policy that maximizes the expected discounted reward.The standard family of algorithms to calculate this optimal policy requires storage for two arrays indexed by state: value
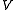 , which contains real values, and policy
, which contains real values, and policy  which contains actions. At the end of the algorithm,
which contains actions. At the end of the algorithm,  will contain the solution and
will contain the solution and 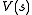 will contain the discounted sum of the rewards to be earned (on average) by following that solution from state
will contain the discounted sum of the rewards to be earned (on average) by following that solution from state  .
.The algorithm has the following two kinds of steps, which are repeated in some order for all the states until no further changes take place.
They are
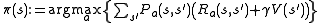
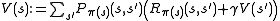
Their order depends on the variant of the algorithm; one can also do them for all states at once or state by state, and more often to some states than others. As long as no state is permanently excluded from either of the steps, the algorithm will eventually arrive at the correct solution.
Value iteration
In value iteration (Bellman 1957), which is also called backward inductionBackward induction
Backward induction is the process of reasoning backwards in time, from the end of a problem or situation, to determine a sequence of optimal actions. It proceeds by first considering the last time a decision might be made and choosing what to do in any situation at that time. Using this...
,
the
 array is not used; instead, the value of
array is not used; instead, the value of 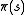 is calculated whenever it is needed. Shapley's 1953 paper on stochastic games included as a special case the value iteration method for MDPs, but this was recognized only later on.
is calculated whenever it is needed. Shapley's 1953 paper on stochastic games included as a special case the value iteration method for MDPs, but this was recognized only later on.Substituting the calculation of
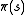 into the calculation of
into the calculation of  gives the combined step:
gives the combined step: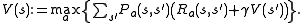
This update rule is iterated for all states
 until it converges with the left-hand side equal to the right-hand side (which is the Bellman equation
until it converges with the left-hand side equal to the right-hand side (which is the Bellman equationBellman equation
A Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
for this problem).
Policy iteration
In policy iteration (Howard 1960), step one is performed once, and then step two is repeated until it converges. Then step one is again performed once and so on.Instead of repeating step two to convergence, it may be formulated and solved as a set of linear equations.
This variant has the advantage that there is a definite stopping condition: when the array
 does not change in the course of applying step 1 to all states, the algorithm is completed.
does not change in the course of applying step 1 to all states, the algorithm is completed.Modified policy iteration
In modified policy iteration (van Nunen, 1976; Puterman and Shin 1978), step one is performed once, and then step two is repeated several times. Then step one is again performed once and so on.Prioritized sweeping
In this variant, the steps are preferentially applied to states which are in some way important - whether based on the algorithm (there were large changes in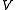 or
or  around those states recently) or based on use (those states are near the starting state, or otherwise of interest to the person or program using the algorithm).
around those states recently) or based on use (those states are near the starting state, or otherwise of interest to the person or program using the algorithm).Extensions and generalizations
A Markov decision process is a stochastic gameStochastic game
In game theory, a stochastic game, introduced by Lloyd Shapley in the early 1950s, is a dynamic game with probabilistic transitions played by one or more players. The game is played in a sequence of stages. At the beginning of each stage the game is in some state...
with only one player.
Partial observability
The solution above assumes that the state is known when action is to be taken; otherwise
is known when action is to be taken; otherwise 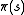 cannot be calculated. When this assumption is not true, the problem is called a partially observable Markov decision process or POMDP.
cannot be calculated. When this assumption is not true, the problem is called a partially observable Markov decision process or POMDP.Reinforcement Learning
If the probabilities or rewards are unknown, the problem is one of reinforcement learningReinforcement learning
Inspired by behaviorist psychology, reinforcement learning is an area of machine learning in computer science, concerned with how an agent ought to take actions in an environment so as to maximize some notion of cumulative reward...
(Sutton and Barto, 1998).
For this purpose it is useful to define a further function, which corresponds to taking the action
 and then continuing optimally (or according to whatever policy one currently has):
and then continuing optimally (or according to whatever policy one currently has):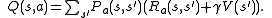
While this function is also unknown, experience during learning is based on
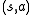 pairs (together with the outcome
pairs (together with the outcome 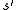 ); that is, "I was in state
); that is, "I was in state  and I tried doing
and I tried doing  and
and 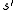 happened"). Thus, one has an array
happened"). Thus, one has an array 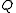 and uses experience to update it directly. This is known as Q-learning
and uses experience to update it directly. This is known as Q-learningQ-learning
Q-learning is a reinforcement learning technique that works by learning an action-value function that gives the expected utility of taking a given action in a given state and following a fixed policy thereafter. One of the strengths of Q-learning is that it is able to compare the expected utility...
.
The power of reinforcement learning lies in its ability to solve the Markov decision process without computing the transition probabilities; note that transition probabilities are needed in value and policy iteration. Also, reinforcement learning can be combined with function approximation, and thereby one can solve problems with a very large number of states. Reinforcement Learning can also be handily performed within Monte Carlo simulators of systems.
Continuous-time Markov Decision Process
In Discrete-time Markov Decision Process, decisions are made at discrete time epoch. However, for Continuous-time Markov Decision Process, decisions can be made at any time when decision maker wants. Different than Discrete-time Markov Decision Process, Continuous-time Markov Decision Process could better model the decision making process when the interested system has continuous dynamics, i.e., the system dynamics is defined by Partial Differential Equations(PDEs).Definition
In order to discuss the Continuous-time Markov Decision Process, we introduce two sets of notations:If the state space and action space are finite,
-
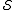 : State space;
: State space; -
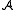 : Action space;
: Action space; -
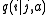 :
:  , transition rate function;
, transition rate function; -
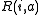 :
: 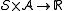 , a reward function.
, a reward function.
If the state space and action space are continuous,
-
 : State space.;
: State space.; -
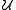 : Space of possible control;
: Space of possible control; -
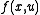 :
: 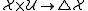 , a transition rate function;
, a transition rate function; -
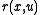 :
: 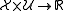 , a reward rate function,(
, a reward rate function,( and
and  is the reward function we discussed in previous case.)
is the reward function we discussed in previous case.)
Problem
Like the Discrete-time Markov Decision Processes, in Continuous-time Markov Decision Process we want to find the optimal policy or control which could give us the optimal expected integrated reward: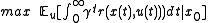
Where
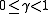
Linear programming formulation
If the state space and action space are finite, we could use linear programming formulation to find the optimal policy, which was one of the earliest solution approaches. Here we only consider the ergodic model, which means our continuous-time MDP become ergodic Continuous-time Markov Chain under stationary policyPolicy
A policy is typically described as a principle or rule to guide decisions and achieve rational outcome. The term is not normally used to denote what is actually done, this is normally referred to as either procedure or protocol...
. Under this assumption, although the decision maker could make decision at any time, on the current state, he could not get more benefit to make more than one actions. It is better for him to take action only at the time when system transit from current state to another state. Under some conditions,(for detail check Corollary 3.14 of Continuous-Time Markov Decision Processes), if our optimal value function
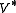 is independent of state i, we will have a following equation:
is independent of state i, we will have a following equation: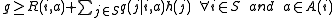
If there exists a function
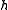 , then
, then  will be the smallest g could satisfied the above equation. In order to find the
will be the smallest g could satisfied the above equation. In order to find the 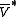 , we could have the following linear programming model:
, we could have the following linear programming model:
- Primal linear program(P-LP)
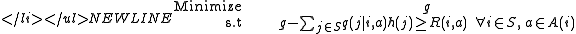
- Dual linear program(D-LP)
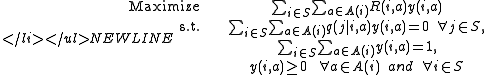
 is a feasible solution to the D-LP if
is a feasible solution to the D-LP if  is
is
nonnative and satisfied the constraints in the D-LP problem. A
feasible solution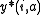 to the D-LP is said to be an optimal
to the D-LP is said to be an optimal
solution if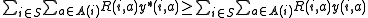
for all feasible solution y(i,a) to the D-LP.
Once we found the optimal solution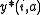 , we could use those optimal solution to establish the optimal policies.
, we could use those optimal solution to establish the optimal policies.
Hamilton-Jacobi-Bellman equation
In Continuous-time MDP, if the state space and action space are continuous, the optimal criterion could be found by solving Hamilton-Jacobi-Bellman partial differential equation.
In order to discuss the HJB equation, we need to reformulate
our problem
D( ) is the terminal reward function,
) is the terminal reward function, 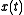 is the
is the
system state vector, is the system control vector we try to
is the system control vector we try to
find. f( ) shows how the state vector change over time.
) shows how the state vector change over time.
Hamilton-Jacobi-Bellman equation is as follows: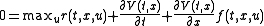
We could solve the equation to find the optimal control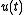 , which could give us the optimal value
, which could give us the optimal value 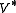
Alternative notations
The terminology and notation for MDPs are not entirely settled. There are two main streams — one focuses on maximization problems from contexts like economics, using the terms action, reward, value and calling the discount factor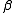 or
or 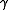 , while the other focuses on minimization problems from engineering and navigation, using the terms control, cost, cost-to-go and calling the discount factor
, while the other focuses on minimization problems from engineering and navigation, using the terms control, cost, cost-to-go and calling the discount factor  . In addition, the notation for the transition probability varies.
. In addition, the notation for the transition probability varies.
in this article alternative comment action 
control 
reward 
cost 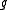
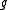 is the negative of
is the negative of 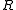
value 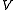
cost-to-go 
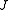 is the negative of
is the negative of 
policy 
policy 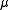
discounting factor 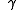
discounting factor 
transition probability 
transition probability 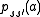
In addition, transition probability is sometimes written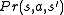 ,
,  or, rarely,
or, rarely, 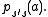
See also
- Partially observable Markov decision processPartially observable Markov decision processA Partially Observable Markov Decision Process is a generalization of a Markov Decision Process. A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state...
- Dynamic programmingDynamic programmingIn mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
- Bellman equationBellman equationA Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
for applications to economics. - Hamilton–Jacobi–Bellman equation
- Optimal controlOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
External links
- MDP Toolbox for Matlab - An excellent tutorial and Matlab toolbox for working with MDPs.
- Reinforcement Learning An Introduction by Richard S. Sutton and Andrew G. Barto
- SPUDD A structured MDP solver for download by Jesse Hoey
- Learning to Solve Markovian Decision Processes by Satinder P. Singh
- Partially observable Markov decision process
- Dual linear program(D-LP)

