
Stochastic game
Encyclopedia
In game theory
, a stochastic game, introduced by Lloyd Shapley
in the early 1950s, is a dynamic game with probabilistic transitions played by one or more players. The game is played in a sequence of stages. At the beginning of each stage the game is in some state. The players select actions and each player receives a payoff that depends on the current state and the chosen actions. The game then moves to a new random state whose distribution depends on the previous state and the actions chosen by the players. The procedure is repeated at the new state and play continues for a finite or infinite number of stages. The total payoff to a player is often taken to be the discounted sum of the stage payoffs or the limit inferior of the averages of the stage payoffs.
Stochastic games generalize both Markov decision process
es and repeated game
s.
 ; a state space
; a state space  (either a finite set or a measurable space
(either a finite set or a measurable space  ); for each player
); for each player  , an action set
, an action set 
(either a finite set or a measurable space ); a transition probability
); a transition probability  from
from  , where
, where 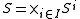 is the action profiles, to
is the action profiles, to  , where
, where 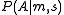 is the probability that the next state is in
is the probability that the next state is in 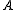 given the current state
given the current state  and the current action profile
and the current action profile  ; and a payoff function
; and a payoff function  from
from  to
to  , where the
, where the 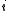 -th coordinate of
-th coordinate of  ,
,  , is the payoff to player
, is the payoff to player  as a function of the state
as a function of the state  and the action profile
and the action profile  .
.
The game starts at some initial state . At stage
. At stage  , players first observe
, players first observe  , then simultaneously choose actions
, then simultaneously choose actions  , then observe the action profile
, then observe the action profile 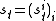 , and then nature selects
, and then nature selects 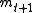 according to the probability
according to the probability  . A play of the stochastic game,
. A play of the stochastic game, 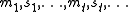 ,
,
defines a stream of payoffs , where
, where  .
.
The discounted game with discount factor
with discount factor  (
( ) is the game where the payoff to player
) is the game where the payoff to player 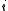 is
is  . The
. The  -stage game
-stage game
is the game where the payoff to player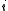 is
is  .
.
The value , respectively
, respectively  , of a two-person zero-sum stochastic game
, of a two-person zero-sum stochastic game  , respectively
, respectively  , with finitely many states and actions exists, and Truman Bewley
, with finitely many states and actions exists, and Truman Bewley
and Elon Kohlberg (1976) proved that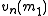 converges to a limit as
converges to a limit as  goes to infinity and that
goes to infinity and that  converges to the same limit as
converges to the same limit as 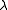 goes to
goes to  .
.
The "undiscounted" game is the game where the payoff to player
is the game where the payoff to player  is the "limit" of the averages of the stage payoffs. Some precautions are needed in defining the value of a two-person zero-sum
is the "limit" of the averages of the stage payoffs. Some precautions are needed in defining the value of a two-person zero-sum 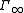 and in defining equilibrium payoffs of a non-zero-sum
and in defining equilibrium payoffs of a non-zero-sum  . The uniform value
. The uniform value  of a two-person zero-sum stochastic game
of a two-person zero-sum stochastic game  exists if for every
exists if for every  there is a positive integer
there is a positive integer  and a strategy pair
and a strategy pair  of player 1 and
of player 1 and  of player 2 such that for every
of player 2 such that for every  and
and  and every
and every  the expectation of
the expectation of  with respect to the probability on plays defined by
with respect to the probability on plays defined by  and
and  is at least
is at least  , and the expectation of
, and the expectation of 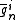 with respect to the probability on plays defined by
with respect to the probability on plays defined by  and
and  is at most
is at most  . Jean Francois Mertens and Abraham Neyman (1981) proved that every two-person zero-sum stochastic game with finitely many states and actions has a uniform value.
. Jean Francois Mertens and Abraham Neyman (1981) proved that every two-person zero-sum stochastic game with finitely many states and actions has a uniform value.
If there is a finite number of players and the action sets and the set of states are finite, then a stochastic game with a finite number of stages always has a Nash equilibrium
. The same is true for a game with infinitely many stages if the total payoff is the discounted sum. Nicolas Vieille has shown that all two-person stochastic games with finite state and action spaces have
approximate Nash equilibria
when the total payoff is the limit inferior of the averages of the stage payoffs. Whether such equilibria exist when there are more than two players is a challenging open question.
s which correspond to the special case where there is only one state.
es and two-person stochastic games. They coin the term Competitive MDPs to encompass both one- and two-player stochastic games.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, a stochastic game, introduced by Lloyd Shapley
Lloyd Shapley
Lloyd Stowell Shapley is a distinguished American mathematician and economist. He is a Professor Emeritus at University of California, Los Angeles, affiliated with departments of Mathematics and Economics...
in the early 1950s, is a dynamic game with probabilistic transitions played by one or more players. The game is played in a sequence of stages. At the beginning of each stage the game is in some state. The players select actions and each player receives a payoff that depends on the current state and the chosen actions. The game then moves to a new random state whose distribution depends on the previous state and the actions chosen by the players. The procedure is repeated at the new state and play continues for a finite or infinite number of stages. The total payoff to a player is often taken to be the discounted sum of the stage payoffs or the limit inferior of the averages of the stage payoffs.
Stochastic games generalize both Markov decision process
Markov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
es and repeated game
Repeated game
In game theory, a repeated game is an extensive form game which consists in some number of repetitions of some base game . The stage game is usually one of the well-studied 2-person games...
s.
Theory
The ingredients of a stochastic game are: a finite set of players ; a state space
; a state space  (either a finite set or a measurable space
(either a finite set or a measurable space  ); for each player
); for each player  , an action set
, an action set 
(either a finite set or a measurable space
 ); a transition probability
); a transition probability  from
from  , where
, where 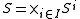 is the action profiles, to
is the action profiles, to  , where
, where 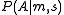 is the probability that the next state is in
is the probability that the next state is in 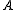 given the current state
given the current state  and the current action profile
and the current action profile  ; and a payoff function
; and a payoff function  from
from  to
to  , where the
, where the 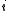 -th coordinate of
-th coordinate of  ,
,  , is the payoff to player
, is the payoff to player  as a function of the state
as a function of the state  and the action profile
and the action profile  .
.The game starts at some initial state
 . At stage
. At stage  , players first observe
, players first observe  , then simultaneously choose actions
, then simultaneously choose actions  , then observe the action profile
, then observe the action profile 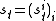 , and then nature selects
, and then nature selects 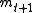 according to the probability
according to the probability  . A play of the stochastic game,
. A play of the stochastic game, 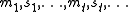 ,
,defines a stream of payoffs
 , where
, where  .
.The discounted game
 with discount factor
with discount factor  (
( ) is the game where the payoff to player
) is the game where the payoff to player 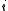 is
is  . The
. The  -stage game
-stage gameis the game where the payoff to player
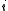 is
is  .
.The value
 , respectively
, respectively  , of a two-person zero-sum stochastic game
, of a two-person zero-sum stochastic game  , respectively
, respectively  , with finitely many states and actions exists, and Truman Bewley
, with finitely many states and actions exists, and Truman BewleyTruman Bewley
Truman Fassett Bewley is an American economist. He is the Alfred Cowles Professor of Economics at Yale University. Originally specializing in mathematical economics and General equilibrium theory, since the late 1990s Bewley has gained renown for his work on sticky wages...
and Elon Kohlberg (1976) proved that
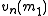 converges to a limit as
converges to a limit as  goes to infinity and that
goes to infinity and that  converges to the same limit as
converges to the same limit as 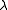 goes to
goes to  .
.The "undiscounted" game
 is the game where the payoff to player
is the game where the payoff to player  is the "limit" of the averages of the stage payoffs. Some precautions are needed in defining the value of a two-person zero-sum
is the "limit" of the averages of the stage payoffs. Some precautions are needed in defining the value of a two-person zero-sum 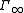 and in defining equilibrium payoffs of a non-zero-sum
and in defining equilibrium payoffs of a non-zero-sum  . The uniform value
. The uniform value  of a two-person zero-sum stochastic game
of a two-person zero-sum stochastic game  exists if for every
exists if for every  there is a positive integer
there is a positive integer  and a strategy pair
and a strategy pair  of player 1 and
of player 1 and  of player 2 such that for every
of player 2 such that for every  and
and  and every
and every  the expectation of
the expectation of  with respect to the probability on plays defined by
with respect to the probability on plays defined by  and
and  is at least
is at least  , and the expectation of
, and the expectation of 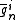 with respect to the probability on plays defined by
with respect to the probability on plays defined by  and
and  is at most
is at most  . Jean Francois Mertens and Abraham Neyman (1981) proved that every two-person zero-sum stochastic game with finitely many states and actions has a uniform value.
. Jean Francois Mertens and Abraham Neyman (1981) proved that every two-person zero-sum stochastic game with finitely many states and actions has a uniform value.If there is a finite number of players and the action sets and the set of states are finite, then a stochastic game with a finite number of stages always has a Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. The same is true for a game with infinitely many stages if the total payoff is the discounted sum. Nicolas Vieille has shown that all two-person stochastic games with finite state and action spaces have
approximate Nash equilibria
Epsilon-equilibrium
In game theory, an epsilon-equilibrium, or near-Nash equilibrium, is a strategy profile that approximately satisfies the condition of Nash equilibrium.- Definition :Given a game and a real non-negative parameter ε, a strategy profile is said to be an...
when the total payoff is the limit inferior of the averages of the stage payoffs. Whether such equilibria exist when there are more than two players is a challenging open question.
Applications
Stochastic games have applications in economics, evolutionary biology and computer networks. They are generalizations of repeated gameRepeated game
In game theory, a repeated game is an extensive form game which consists in some number of repetitions of some base game . The stage game is usually one of the well-studied 2-person games...
s which correspond to the special case where there is only one state.
Referring book
The most complete reference is the book of articles edited by Neyman and Sorin. The more elementary book of Filar and Vrieze provides a unified rigorous treatment of the theories of Markov Decision ProcessMarkov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
es and two-person stochastic games. They coin the term Competitive MDPs to encompass both one- and two-player stochastic games.

