
Epsilon-equilibrium
Encyclopedia
In game theory
, an epsilon-equilibrium, or near-Nash equilibrium, is a strategy profile that approximately satisfies the condition of Nash equilibrium
.
ε-equilibrium if it is not possible for any player to gain more than ε in expected payoff
by unilaterally deviating from his strategy
. Every Nash Equilibrium
is equivalent to
a ε-equilibrium where ε = 0.
Formally, let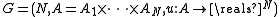 be a N-player game with action sets
be a N-player game with action sets 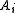 for each player and utility function u. A vector of strategies
for each player and utility function u. A vector of strategies 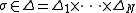 is an
is an  -Nash Equilibrium for G if
-Nash Equilibrium for G if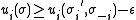 for all
for all 
stochastic game
s of potentially infinite duration. There are
simple examples of stochastic games with no Nash equilibrium
but with an ε-equilibrium for any ε strictly bigger than 0.
Perhaps the simplest such example is the following variant of Matching Pennies
, suggested by Everett. Player 1 hides a penny and
Player 2 must guess if it is heads up or tails up. If Player 2 guesses correctly, he
wins the penny from Player 1 and the game ends. If Player 2 incorrectly guesses that the penny
is heads up,
the game ends with payoff zero to both players. If he incorrectly guesses that it is tails up, the game repeats. If the play continues forever, the payoff to both players is zero.
Given a parameter ε > 0, any strategy profile where Player 2 guesses heads up with
probability ε and tails up with probability 1-ε (at every stage of the game, and independently
from previous stages) is an ε-equilibrium for the game. The expected payoff of Player 2 in
such a strategy profile is at least 1-ε. However, it is easy to see that there is no
strategy for Player 2 that can guarantee an expected payoff of exactly 1. Therefore, the game
has no Nash equilibrium
.
Another simple example is the finitely repeated prisoner's dilemma for T periods, where the payoff is averaged over the T periods. The only Nash equilibrium
of this game is to choose Defect in each period. Now consider the two strategies tit-for-tat and grim trigger
. Although neither tit-for-tat nor grim trigger
are Nash equilibria for the game, both of them are -equilibria for some positive
-equilibria for some positive  . The acceptable values of
. The acceptable values of  depend on the payoffs of the consituent game and on the number T of periods.
depend on the payoffs of the consituent game and on the number T of periods.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, an epsilon-equilibrium, or near-Nash equilibrium, is a strategy profile that approximately satisfies the condition of Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
.
Definition
Given a game and a real non-negative parameter ε, a strategy profile is said to be anε-equilibrium if it is not possible for any player to gain more than ε in expected payoff
by unilaterally deviating from his strategy
Strategy
Strategy, a word of military origin, refers to a plan of action designed to achieve a particular goal. In military usage strategy is distinct from tactics, which are concerned with the conduct of an engagement, while strategy is concerned with how different engagements are linked...
. Every Nash Equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
is equivalent to
a ε-equilibrium where ε = 0.
Formally, let
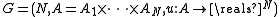 be a N-player game with action sets
be a N-player game with action sets 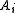 for each player and utility function u. A vector of strategies
for each player and utility function u. A vector of strategies 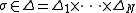 is an
is an  -Nash Equilibrium for G if
-Nash Equilibrium for G if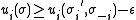 for all
for all 
Example
The notion of ε-equilibria is important in the theory ofstochastic game
Stochastic game
In game theory, a stochastic game, introduced by Lloyd Shapley in the early 1950s, is a dynamic game with probabilistic transitions played by one or more players. The game is played in a sequence of stages. At the beginning of each stage the game is in some state...
s of potentially infinite duration. There are
simple examples of stochastic games with no Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
but with an ε-equilibrium for any ε strictly bigger than 0.
Perhaps the simplest such example is the following variant of Matching Pennies
Matching pennies
Matching pennies is the name for a simple example game used in game theory. It is the two strategy equivalent of Rock, Paper, Scissors. Matching pennies is used primarily to illustrate the concept of mixed strategies and a mixed strategy Nash equilibrium....
, suggested by Everett. Player 1 hides a penny and
Player 2 must guess if it is heads up or tails up. If Player 2 guesses correctly, he
wins the penny from Player 1 and the game ends. If Player 2 incorrectly guesses that the penny
is heads up,
the game ends with payoff zero to both players. If he incorrectly guesses that it is tails up, the game repeats. If the play continues forever, the payoff to both players is zero.
Given a parameter ε > 0, any strategy profile where Player 2 guesses heads up with
probability ε and tails up with probability 1-ε (at every stage of the game, and independently
from previous stages) is an ε-equilibrium for the game. The expected payoff of Player 2 in
such a strategy profile is at least 1-ε. However, it is easy to see that there is no
strategy for Player 2 that can guarantee an expected payoff of exactly 1. Therefore, the game
has no Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
.
Another simple example is the finitely repeated prisoner's dilemma for T periods, where the payoff is averaged over the T periods. The only Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
of this game is to choose Defect in each period. Now consider the two strategies tit-for-tat and grim trigger
Grim trigger
In game theory, grim trigger is a trigger strategy for a repeated game, such as an iterated prisoner's dilemma. Initially, a player using grim trigger will cooperate, but as soon as the opponent defects , the player using grim trigger will defect for the remainder of the iterated game...
. Although neither tit-for-tat nor grim trigger
Grim trigger
In game theory, grim trigger is a trigger strategy for a repeated game, such as an iterated prisoner's dilemma. Initially, a player using grim trigger will cooperate, but as soon as the opponent defects , the player using grim trigger will defect for the remainder of the iterated game...
are Nash equilibria for the game, both of them are
 -equilibria for some positive
-equilibria for some positive  . The acceptable values of
. The acceptable values of  depend on the payoffs of the consituent game and on the number T of periods.
depend on the payoffs of the consituent game and on the number T of periods.

