Bellman equation
Encyclopedia
A Bellman equation named after its discoverer, Richard Bellman
, is a necessary condition for optimality associated with the mathematical optimization
method known as dynamic programming
. It writes the value of a decision problem at a certain point in time in terms of the payoff from some initial choices and the value of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into simpler subproblems, as Bellman's Principle of Optimality prescribes.
The Bellman equation was first applied to engineering control theory
and to other topics in applied mathematics, and subsequently became an important tool in economic theory.
Almost any problem which can be solved using optimal control theory can also be solved by analyzing the appropriate Bellman equation. However, the term 'Bellman equation' usually refers to the dynamic programming equation associated with discrete-time optimization problems. In continuous-time optimization problems, the analogous equation is a partial differential equation
which is usually called the Hamilton-Jacobi-Bellman equation
.
Dynamic programming breaks a multi-period planning problem into simpler steps at different points in time. Therefore, it requires keeping track of how the decision situation is evolving over time. The information about the current situation which is needed to make a correct decision is called the state (See Bellman, 1957, Ch. III.2). For example, to decide how much to consume and spend at each point in time, people would need to know (among other things) their initial wealth. Therefore, wealth would be one of their state variable
s, but there would probably be others.
The variables chosen at any given point in time are often called the control variables. For example, given their current wealth, people might decide how much to consume now. Choosing the control variables now may be equivalent to choosing the next state; more generally, the next state is affected by other factors in addition to the current control. For example, in the simplest case, today's wealth (the state) and consumption (the control) might exactly determine tomorrow's wealth (the new state), though typically other factors will affect tomorrow's wealth too.
The dynamic programming approach describes the optimal plan by finding a rule that tells what the controls should be, given any possible value of the state. For example, if consumption (c) depends only on wealth (W), we would seek a rule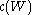
that gives consumption as a function of wealth. Such a rule, determining the controls as a function of the states, is called a policy function (See Bellman, 1957, Ch. III.2).
Finally, by definition, the optimal decision rule is the one that achieves the best possible value of the objective. For example, if someone chooses consumption, given wealth, in order to maximize happiness (assuming happiness H can be represented by a mathematical function, such as a utility
function), then each level of wealth will be associated with some highest possible level of happiness,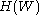
. The best possible value of the objective, written as a function of the state, is called the value function.
Richard Bellman
showed that a dynamic optimization
problem in discrete time
can be stated in a recursive
, step-by-step form by writing down the relationship between the value function in one period and the value function in the next period. The relationship between these two value functions is called the Bellman equation.
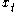. For a decision that begins at time 0, we take as given the initial state 
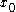. At any time, the set of possible actions depends on the current state; we can write this as 
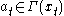, where the action 
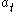represents one or more control variables. We also assume that the state changes from x to a new state T(x,a) when action a is taken, and that the current payoff from taking action a in state x is F(x,a). Finally, we assume impatience, represented by a discount factor 0<β<1.
Under these assumptions, an infinite-horizon decision problem takes the following form:
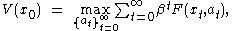
subject to the constraints
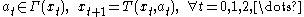
Notice that we have defined notation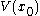
to represent the optimal value that can be obtained by maximizing this objective function subject to the assumed constraints. This function is the value function. It is a function of the initial state variable 
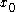, since the best value obtainable depends on the initial situation.
In computer science, a problem that can be broken apart like this is said to have optimal substructure
. In the context of dynamic game theory
, this principle is analogous to the concept of subgame perfect equilibrium
, although what constitutes an optimal policy in this case is conditioned on the decision-maker's opponents choosing similarly optimal policies from their points of view.
As suggested by the Principle of Optimality, we will consider the first decision separately, setting aside all future decisions (we will start afresh from time 1 with the new state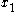
). Collecting the future decisions in brackets on the right, the previous problem is equivalent to:
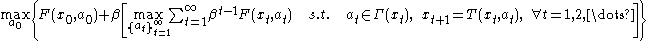
subject to the constraints
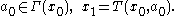
Here we are choosing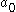
, knowing that our choice will cause the time 1 state to be 
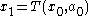. That new state will then affect the decision problem from time 1 on. The whole future decision problem appears inside the square brackets on the right.
.
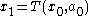Therefore we can rewrite the problem as a recursive
definition of the value function:
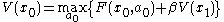, subject to the constraints: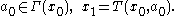 
This is the Bellman equation. It can be simplified even further if we drop time subscripts and plug in the value of the next state:
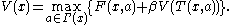
The Bellman equation is classified as a functional equation
, because solving it means finding the unknown function V, which is the value function. Recall that the value function describes the best possible value of the objective, as a function of the state x. By calculating the value function, we will also find the function a(x) that describes the optimal action as a function of the state; this is called the policy function.
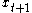is a random variable, which may be influenced by 
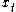and 
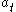, but is not determined by them exactly. We can describe this case by defining the probability distribution
conditional on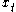
and 
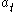, for example,
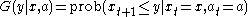
Given this probability law determining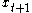
conditional on 
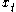and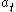 
, the Bellman equation can be written as
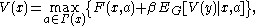
where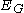
represents a conditional expectation
under distribution G.
A celebrated economic application of a Bellman equation is Merton's seminal 1973 article on the intertemporal capital asset pricing model. (See also Merton's portfolio problem
).The solution to Merton's theoretical model, one in which investors chose between income today and future income or capital gains, is a form of Bellman's equation. Because economic applications of dynamic programming usually result in a Bellman equation that is a difference equation, economists refer to dynamic programming as a "recursive method."
Stokey, Lucas & Prescott describes stochastic and nonstochastic dynamic programming in considerable detail, giving many examples of how to employ dynamic programming to solve problems in economic theory. This book led to dynamic programming being employed to solve a wide range of theoretical problems in economics, including optimal economic growth
, resource extraction
, principal–agent problems, public finance
, business investment
, asset pricing, factor supply, and industrial organization
. Ljungqvist & Sargent apply dynamic programming to study a variety of theoretical questions in monetary policy
, fiscal policy
, taxation, economic growth
, search theory
, and labor economics. Dixit & Pindyck showed the value of the method for thinking about capital budgeting
. Anderson adapted the technique to business valuation, including privately-held businesses.
Using dynamic programming to solve concrete problems is complicated by informational difficulties, such as choosing the unobservable discount rate. There are also computational issues, the main one being the curse of dimensionality
arising from the vast number of possible actions and potential state variables that must be considered before an optimal strategy can be selected. For an extensive discussion of computational issues, see Miranda & Fackler., and Meyn 2007
, a Bellman equation refers to a recursion
for expected rewards. For example, the expected reward for being in a particular state s and following some fixed policy
has the Bellman equation:
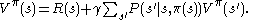
This equation describes the expected reward for taking the action prescribed by some policy
.
The equation for the optimal policy is referred to as the Bellman optimality equation:
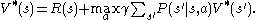
It describes the reward for taking the action giving the highest expected return.
Richard Bellman
Richard Ernest Bellman was an American applied mathematician, celebrated for his invention of dynamic programming in 1953, and important contributions in other fields of mathematics.-Biography:...
, is a necessary condition for optimality associated with the mathematical optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
method known as dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
. It writes the value of a decision problem at a certain point in time in terms of the payoff from some initial choices and the value of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into simpler subproblems, as Bellman's Principle of Optimality prescribes.
The Bellman equation was first applied to engineering control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
and to other topics in applied mathematics, and subsequently became an important tool in economic theory.
Almost any problem which can be solved using optimal control theory can also be solved by analyzing the appropriate Bellman equation. However, the term 'Bellman equation' usually refers to the dynamic programming equation associated with discrete-time optimization problems. In continuous-time optimization problems, the analogous equation is a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
which is usually called the Hamilton-Jacobi-Bellman equation
Hamilton-Jacobi-Bellman equation
The Hamilton–Jacobi–Bellman equation is a partial differential equation which is central to optimal control theory. The solution of the HJB equation is the 'value function', which gives the optimal cost-to-go for a given dynamical system with an associated cost function.When solved locally, the...
.
Analytical concepts in dynamic programming
To understand the Bellman equation, several underlying concepts must be understood. First, any optimization problem has some objective--- minimizing travel time, minimizing cost, maximizing profits, maximizing utility, et cetera. The mathematical function that describes this objective is called the objective function.Dynamic programming breaks a multi-period planning problem into simpler steps at different points in time. Therefore, it requires keeping track of how the decision situation is evolving over time. The information about the current situation which is needed to make a correct decision is called the state (See Bellman, 1957, Ch. III.2). For example, to decide how much to consume and spend at each point in time, people would need to know (among other things) their initial wealth. Therefore, wealth would be one of their state variable
State variable
A state variable is one of the set of variables that describe the "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour...
s, but there would probably be others.
The variables chosen at any given point in time are often called the control variables. For example, given their current wealth, people might decide how much to consume now. Choosing the control variables now may be equivalent to choosing the next state; more generally, the next state is affected by other factors in addition to the current control. For example, in the simplest case, today's wealth (the state) and consumption (the control) might exactly determine tomorrow's wealth (the new state), though typically other factors will affect tomorrow's wealth too.
The dynamic programming approach describes the optimal plan by finding a rule that tells what the controls should be, given any possible value of the state. For example, if consumption (c) depends only on wealth (W), we would seek a rule
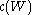that gives consumption as a function of wealth. Such a rule, determining the controls as a function of the states, is called a policy function (See Bellman, 1957, Ch. III.2).Finally, by definition, the optimal decision rule is the one that achieves the best possible value of the objective. For example, if someone chooses consumption, given wealth, in order to maximize happiness (assuming happiness H can be represented by a mathematical function, such as a utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
function), then each level of wealth will be associated with some highest possible level of happiness,
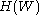. The best possible value of the objective, written as a function of the state, is called the value function.Richard Bellman
Richard Bellman
Richard Ernest Bellman was an American applied mathematician, celebrated for his invention of dynamic programming in 1953, and important contributions in other fields of mathematics.-Biography:...
showed that a dynamic optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
problem in discrete time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
can be stated in a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
, step-by-step form by writing down the relationship between the value function in one period and the value function in the next period. The relationship between these two value functions is called the Bellman equation.
A dynamic decision problem
Let the state at time t be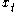. For a decision that begins at time 0, we take as given the initial state 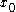. At any time, the set of possible actions depends on the current state; we can write this as 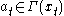, where the action 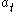represents one or more control variables. We also assume that the state changes from x to a new state T(x,a) when action a is taken, and that the current payoff from taking action a in state x is F(x,a). Finally, we assume impatience, represented by a discount factor 0<β<1.Under these assumptions, an infinite-horizon decision problem takes the following form:
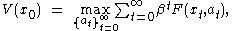
subject to the constraints
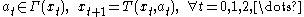
Notice that we have defined notation
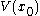to represent the optimal value that can be obtained by maximizing this objective function subject to the assumed constraints. This function is the value function. It is a function of the initial state variable 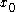, since the best value obtainable depends on the initial situation.Bellman's Principle of Optimality
The dynamic programming method breaks this decision problem into smaller subproblems. Richard Bellman's Principle of Optimality describes how to do this:Principle of Optimality: An optimal policy has the property that whatever the initial state and initial decision are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision. (See Bellman, 1957, Chap. III.3.)
In computer science, a problem that can be broken apart like this is said to have optimal substructure
Optimal substructure
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions to its subproblems...
. In the context of dynamic game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, this principle is analogous to the concept of subgame perfect equilibrium
Subgame perfect equilibrium
In game theory, a subgame perfect equilibrium is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game...
, although what constitutes an optimal policy in this case is conditioned on the decision-maker's opponents choosing similarly optimal policies from their points of view.
As suggested by the Principle of Optimality, we will consider the first decision separately, setting aside all future decisions (we will start afresh from time 1 with the new state
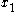). Collecting the future decisions in brackets on the right, the previous problem is equivalent to: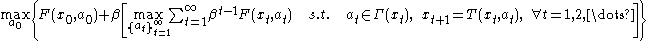subject to the constraints
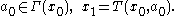
Here we are choosing
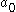, knowing that our choice will cause the time 1 state to be 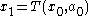. That new state will then affect the decision problem from time 1 on. The whole future decision problem appears inside the square brackets on the right.The Bellman equation
So far it seems we have only made the problem uglier by separating today's decision from future decisions. But we can simplify by noticing that what is inside the square brackets on the right is the value of the time 1 decision problem, starting from state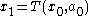.Therefore we can rewrite the problem as a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
definition of the value function:
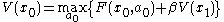, subject to the constraints: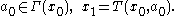 This is the Bellman equation. It can be simplified even further if we drop time subscripts and plug in the value of the next state:
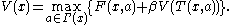
The Bellman equation is classified as a functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
, because solving it means finding the unknown function V, which is the value function. Recall that the value function describes the best possible value of the objective, as a function of the state x. By calculating the value function, we will also find the function a(x) that describes the optimal action as a function of the state; this is called the policy function.
The Bellman equation in a stochastic problem
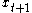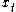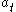Dynamic programming can be especially useful in stochastic decisions, that is, optimization problems affected by random events. For example, consider a problem exactly like the one discussed above, except that is a random variable, which may be influenced by and , but is not determined by them exactly. We can describe this case by defining the probability distributionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
conditional on
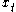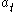and , for example,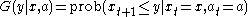Given this probability law determining
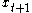conditional on 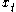and 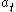, the Bellman equation can be written as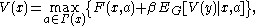where
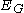represents a conditional expectationConditional expectation
In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
under distribution G.
Solution methods
- The method of undetermined coefficientsMethod of undetermined coefficientsIn mathematics, the method of undetermined coefficients, also known as the lucky guess method, is an approach to finding a particular solution to certain inhomogeneous ordinary differential equations and recurrence relations...
, also known as 'guess and verify', can be used to solve some infinite-horizon, autonomousAutonomous system (mathematics)In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable...
Bellman equations.
- The Bellman equation can be solved by backwards induction, either analyticallyClosed-form expressionIn mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
in a few special cases, or numericallyNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
on a computer. Numerical backwards induction is applicable to a wide variety of problems, but may be infeasible when there are many state variables, due to the curse of dimensionalityCurse of dimensionalityThe curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
.
- By calculating the first-order conditions associated with the Bellman equation, and then using the envelope theoremEnvelope theoremThe envelope theorem is a theorem about optimization problems in microeconomics. It may be used to prove Hotelling's lemma, Shephard's lemma, and Roy's identity...
to eliminate the derivatives of the value function, it is possible to obtain a system of difference equations or differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s called the 'Euler equationEuler-Lagrange equationIn calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
s'. Standard techniques for the solution of difference or differential equations can then be used to calculate the dynamics of the state variables and the control variables of the optimization problem.
Applications in economics
The first known application of a Bellman equation in economics is due to Martin Beckmann and Richard Muth. Martin Beckmann also wrote extensively on consumption theory using the Bellman equation in 1959. His work influenced Edmund S. Phelps, among others.A celebrated economic application of a Bellman equation is Merton's seminal 1973 article on the intertemporal capital asset pricing model. (See also Merton's portfolio problem
Merton's portfolio problem
Merton's Portfolio Problem is a well known problem in continuous-time finance. An investor with a finite lifetime must choose how much to consume and must allocate his wealth between stocks and a risk-free asset so as to maximize expected lifetime utility. The problem was formulated and solved by...
).The solution to Merton's theoretical model, one in which investors chose between income today and future income or capital gains, is a form of Bellman's equation. Because economic applications of dynamic programming usually result in a Bellman equation that is a difference equation, economists refer to dynamic programming as a "recursive method."
Stokey, Lucas & Prescott describes stochastic and nonstochastic dynamic programming in considerable detail, giving many examples of how to employ dynamic programming to solve problems in economic theory. This book led to dynamic programming being employed to solve a wide range of theoretical problems in economics, including optimal economic growth
Economic growth
In economics, economic growth is defined as the increasing capacity of the economy to satisfy the wants of goods and services of the members of society. Economic growth is enabled by increases in productivity, which lowers the inputs for a given amount of output. Lowered costs increase demand...
, resource extraction
Resource extraction
The related terms natural resource extraction both refer to the practice of locating, acquiring and selling natural resources....
, principal–agent problems, public finance
Public finance
Public finance is the revenue and expenditure of public authoritiesThe purview of public finance is considered to be threefold: governmental effects on efficient allocation of resources, distribution of income, and macroeconomic stabilization.-Overview:The proper role of government provides a...
, business investment
Investment
Investment has different meanings in finance and economics. Finance investment is putting money into something with the expectation of gain, that upon thorough analysis, has a high degree of security for the principal amount, as well as security of return, within an expected period of time...
, asset pricing, factor supply, and industrial organization
Industrial organization
Industrial organization is the field of economics that builds on the theory of the firm in examining the structure of, and boundaries between, firms and markets....
. Ljungqvist & Sargent apply dynamic programming to study a variety of theoretical questions in monetary policy
Monetary policy
Monetary policy is the process by which the monetary authority of a country controls the supply of money, often targeting a rate of interest for the purpose of promoting economic growth and stability. The official goals usually include relatively stable prices and low unemployment...
, fiscal policy
Fiscal policy
In economics and political science, fiscal policy is the use of government expenditure and revenue collection to influence the economy....
, taxation, economic growth
Economic growth
In economics, economic growth is defined as the increasing capacity of the economy to satisfy the wants of goods and services of the members of society. Economic growth is enabled by increases in productivity, which lowers the inputs for a given amount of output. Lowered costs increase demand...
, search theory
Search theory
In microeconomics, search theory studies buyers or sellers who cannot instantly find a trading partner, and must therefore search for a partner prior to transacting....
, and labor economics. Dixit & Pindyck showed the value of the method for thinking about capital budgeting
Capital budgeting
Capital budgeting is the planning process used to determine whether an organization's long term investments such as new machinery, replacement machinery, new plants, new products, and research development projects are worth pursuing...
. Anderson adapted the technique to business valuation, including privately-held businesses.
Using dynamic programming to solve concrete problems is complicated by informational difficulties, such as choosing the unobservable discount rate. There are also computational issues, the main one being the curse of dimensionality
Curse of dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
arising from the vast number of possible actions and potential state variables that must be considered before an optimal strategy can be selected. For an extensive discussion of computational issues, see Miranda & Fackler., and Meyn 2007
Example
In MDPMarkov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
, a Bellman equation refers to a recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
for expected rewards. For example, the expected reward for being in a particular state s and following some fixed policy
has the Bellman equation: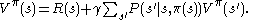This equation describes the expected reward for taking the action prescribed by some policy
.The equation for the optimal policy is referred to as the Bellman optimality equation:
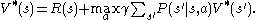
It describes the reward for taking the action giving the highest expected return.
See also
- Dynamic programmingDynamic programmingIn mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
- Hamilton-Jacobi-Bellman equationHamilton-Jacobi-Bellman equationThe Hamilton–Jacobi–Bellman equation is a partial differential equation which is central to optimal control theory. The solution of the HJB equation is the 'value function', which gives the optimal cost-to-go for a given dynamical system with an associated cost function.When solved locally, the...
- Markov decision processMarkov decision processMarkov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
- Optimal control theory
- Optimal substructureOptimal substructureIn computer science, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions to its subproblems...
- Recursive competitive equilibriumRecursive competitive equilibriumIn macroeconomics, recursive competitive equilibrium is an equilibrium concept. It has been widely used in exploring a wide variety of economic issues including business-cycle fluctuations, monetary and fiscal policy, trade related phenomena, and regularities in asset price co-movements...