
Optimal substructure
Encyclopedia
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions to its subproblems. This property is used to determine the usefulness of dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
and greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
s in a problem.
Typically, a greedy algorithm is used to solve a problem with optimal substructure if it can be proved by induction that this is optimal at each step (Cormen et al. pp. 381–2). Otherwise, providing the problem exhibits overlapping subproblem
Overlapping subproblem
In computer science, a problem is said to have overlapping subproblems if the problem can be broken down into subproblems which are reused several times or a recursive algorithm for the problem solves the same subproblem over and over rather than always generating new subproblem.For example, the...
s as well, dynamic programming is used. If there are no appropriate greedy algorithms and the problem fails to exhibit overlapping subproblems, often a lengthy but straightforward search of the solution space is the best alternative.
In the application of dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
to mathematical optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, Richard Bellman
Richard Bellman
Richard Ernest Bellman was an American applied mathematician, celebrated for his invention of dynamic programming in 1953, and important contributions in other fields of mathematics.-Biography:...
's Principle of Optimality is based on the idea that in order to solve a dynamic optimization problem from some starting period t to some ending period T, one implicitly has to solve subproblems starting from later dates s, where t
Bellman equation
A Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
, which shows how the value of the problem starting from t is related to the value of the problem starting from s.
Example
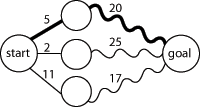
Consider finding a shortest pathShortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
for travelling between two cities by car, as illustrated in Figure 1. Such an example is likely to exhibit optimal substructure. That is, if the shortest route from Seattle to Los Angeles passes through Portland and then Sacramento, then the shortest route from Portland to Los Angeles must pass through Sacramento too. That is, the problem of how to get from Portland to Los Angeles is nested inside the problem of how to get from Seattle to Los Angeles. (The wavy lines in the graph represent solutions to the subproblems.)
As an example of a problem that is unlikely to exhibit optimal substructure, consider the problem of finding the cheapest airline ticket from Buenos Aires to Moscow. Even if that ticket involves stops in Miami and then London, we can't conclude that the cheapest ticket from Miami to Moscow stops in London, because the price at which an airline sells a multi-flight trip is usually not the sum of the prices at which it would sell the individual flights in the trip.
Definition
A slightly more formal definition of optimal substructure can be given. Let a "problem" be a collection of "alternatives", and let each alternative have an associated cost, c(a). The task is to find a set of alternatives that minimizes c(a). Suppose that the alternatives can be partitioned into subsets, where each subset has its own cost function, and each alternative belongs to only one subset. The minima of each of these cost functions can be found, as can the minima of the global cost function, restricted to the same subsets. If these minima match for each subset, then it's almost obvious that a global minimum can be picked not out of the full set of alternatives, but out of only the set that consists of the minima of the smaller, local cost functions we have defined. If minimizing the local functions is a problem of "lower order", and (specifically) if, after a finite number of these reductions, the problem becomes trivial, then the problem has an optimal substructure.Problems with optimal substructure
- Longest common subsequence problemLongest common subsequence problemThe longest common subsequence problem is to find the longest subsequence common to all sequences in a set of sequences . Note that subsequence is different from a substring, see substring vs. subsequence...
- Mergesort
- Quicksort

