Subgame perfect equilibrium
Encyclopedia
In game theory
, a subgame perfect equilibrium (or subgame perfect Nash equilibrium) is a refinement
of a Nash equilibrium
used in dynamic games. A strategy profile
is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame
of the original game. More informally, this means that if (1) the players played any smaller game that consisted of only one part of the larger game and (2) their behavior represents a Nash equilibrium of that smaller game, then their behavior is a subgame perfect equilibrium of the larger game. It is well-known that every finite extensive game has a subgame
perfect equilibrium .
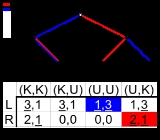
A common method for determining subgame perfect equilibria in the case of a finite game is backward induction
. Here one first considers the last actions of the game and determines which actions the final mover should take in each possible circumstance to maximize his/her utility
. One then supposes that the last actor will do these actions, and considers the second to last actions, again choosing those that maximize that actor's utility. This process continues until one reaches the first move of the game. The strategies which remain are the set of all subgame perfect equilibria for finite-horizon extensive games of perfect information. However, backward induction cannot be applied to games of imperfect or incomplete information because this entails cutting through non-singleton information sets.
The set of subgame perfect equilibria for a given game is always a subset of the set of Nash equilibria for that game. In some cases the sets can be identical.
The Ultimatum game
provides an intuitive example of a game with fewer subgame perfect equilibria than Nash equilibria.
" from the various ultimate outcomes of the game, eliminating branches which would involve any player making a move that is not credible (because it is not optimal) from that node
. One game in which the backward induction solution is well known is tic-tac-toe
, but in theory even Go
has such an optimum strategy for all players.
The interesting aspect of the word "credible" in the preceding paragraph is that taken as a whole (disregarding the irreversibility of reaching sub-games) strategies exist which are superior to subgame perfect strategies, but which are not credible in the sense that a threat to carry them out will harm the player making the threat and prevent that combination of strategies. For instance in the game of "chicken
" if one player has the option of ripping the steering wheel from their car they should always take it because it leads to a "sub game" in which their rational opponent is precluded from doing the same thing (and killing them both). The wheel-ripper will always win the game (making his opponent swerve away), and the opponent's threat to suicidally follow suit is not credible. In fact, having seen the first player discard any means of steering his car, the second player's rational options are reduced from ", " to "", leading to a subgame perfect Nash equilibrium.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, a subgame perfect equilibrium (or subgame perfect Nash equilibrium) is a refinement
Solution concept
In game theory, a solution concept is a formal rule for predicting how the game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players, therefore predicting the result of the game...
of a Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
used in dynamic games. A strategy profile
Strategy (game theory)
In game theory, a player's strategy in a game is a complete plan of action for whatever situation might arise; this fully determines the player's behaviour...
is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame
Subgame
In game theory, a subgame is any part of a game that meets the following criteria :#It has a single initial node that is the only member of that node's information set In game theory, a subgame is any part (a subset) of a game that meets the following criteria (the following terms allude to a game...
of the original game. More informally, this means that if (1) the players played any smaller game that consisted of only one part of the larger game and (2) their behavior represents a Nash equilibrium of that smaller game, then their behavior is a subgame perfect equilibrium of the larger game. It is well-known that every finite extensive game has a subgame
Subgame
In game theory, a subgame is any part of a game that meets the following criteria :#It has a single initial node that is the only member of that node's information set In game theory, a subgame is any part (a subset) of a game that meets the following criteria (the following terms allude to a game...
perfect equilibrium .
A common method for determining subgame perfect equilibria in the case of a finite game is backward induction
Backward induction
Backward induction is the process of reasoning backwards in time, from the end of a problem or situation, to determine a sequence of optimal actions. It proceeds by first considering the last time a decision might be made and choosing what to do in any situation at that time. Using this...
. Here one first considers the last actions of the game and determines which actions the final mover should take in each possible circumstance to maximize his/her utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
. One then supposes that the last actor will do these actions, and considers the second to last actions, again choosing those that maximize that actor's utility. This process continues until one reaches the first move of the game. The strategies which remain are the set of all subgame perfect equilibria for finite-horizon extensive games of perfect information. However, backward induction cannot be applied to games of imperfect or incomplete information because this entails cutting through non-singleton information sets.
The set of subgame perfect equilibria for a given game is always a subset of the set of Nash equilibria for that game. In some cases the sets can be identical.
The Ultimatum game
Ultimatum game
The ultimatum game is a game often played in economic experiments in which two players interact to decide how to divide a sum of money that is given to them. The first player proposes how to divide the sum between the two players, and the second player can either accept or reject this proposal. ...
provides an intuitive example of a game with fewer subgame perfect equilibria than Nash equilibria.
Finding subgame-perfect equilibria
The subgame-perfect Nash equilibrium is normally deduced by "backward inductionBackward induction
Backward induction is the process of reasoning backwards in time, from the end of a problem or situation, to determine a sequence of optimal actions. It proceeds by first considering the last time a decision might be made and choosing what to do in any situation at that time. Using this...
" from the various ultimate outcomes of the game, eliminating branches which would involve any player making a move that is not credible (because it is not optimal) from that node
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
. One game in which the backward induction solution is well known is tic-tac-toe
Tic-tac-toe
Tic-tac-toe, also called wick wack woe and noughts and crosses , is a pencil-and-paper game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The X player usually goes first...
, but in theory even Go
Go (board game)
Go , is an ancient board game for two players that originated in China more than 2,000 years ago...
has such an optimum strategy for all players.
The interesting aspect of the word "credible" in the preceding paragraph is that taken as a whole (disregarding the irreversibility of reaching sub-games) strategies exist which are superior to subgame perfect strategies, but which are not credible in the sense that a threat to carry them out will harm the player making the threat and prevent that combination of strategies. For instance in the game of "chicken
Chicken (game)
The game of chicken, also known as the hawk-dove or snowdrift game, is an influential model of conflict for two players in game theory...
" if one player has the option of ripping the steering wheel from their car they should always take it because it leads to a "sub game" in which their rational opponent is precluded from doing the same thing (and killing them both). The wheel-ripper will always win the game (making his opponent swerve away), and the opponent's threat to suicidally follow suit is not credible. In fact, having seen the first player discard any means of steering his car, the second player's rational options are reduced from "
See also
- ChessChessChess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
- Centipede gameCentipede gameIn game theory, the centipede game, first introduced by Rosenthal , is an extensive form game in which two players take turns choosing either to take a slightly larger share of a slowly increasing pot, or to pass the pot to the other player...
- Solution conceptSolution conceptIn game theory, a solution concept is a formal rule for predicting how the game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players, therefore predicting the result of the game...
- Glossary of game theory
- Dynamic inconsistencyDynamic inconsistencyIn economics, dynamic inconsistency, or time inconsistency, describes a situation where a decision-maker's preferences change over time in such a way that what is preferred at one point in time is inconsistent with what is preferred at another point in time...
- John Forbes NashJohn Forbes NashJohn Forbes Nash, Jr. is an American mathematician whose works in game theory, differential geometry, and partial differential equations have provided insight into the forces that govern chance and events inside complex systems in daily life...
- Minimax theorem

