Convexity in economics
Encyclopedia
Convexity is an important topic in economics. In the Arrow-Debreu model
of general economic equilibrium
, agents have convex budget set
s and convex preferences
: At equilibrium prices, the budget hyperplane supports
the best attainable indifference curve
. The profit function
is the convex conjugate
of the cost function. Convex analysis
is the standard tool for analyzing textbook economics. Non-convex phenomena in economics have been studied with nonsmooth analysis, which generalizes convex analysis
.
.
vector space
of two dimension
s may be given a Cartesian coordinate system
in which every point is identified by a list of two real numbers, called "coordinates", which are conventionally denoted by x and y. Two points in the Cartesian plane can be added coordinate-wise
further, a point can be multiplied
by each real number λ coordinate-wise
More generally, any real vector space of (finite) dimension D can be viewed as the set of all possible lists of D real numbers } together with two operation
s: vector addition and multiplication by a real number
. For finite-dimensional vector spaces, the operations of vector addition and real-number multiplication can each be defined coordinate-wise, following the example of the Cartesian plane.
In a real vector space, a set is defined to be convex
if, for each pair of its points, every point on the line segment
that joins them is covered by the set. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent
shape, is non-convex. Trivially
, the empty set
is convex.
More formally, a set Q is convex if, for all points v0 and v1 in Q and for every real number λ in the unit interval
[0,1], the point
is a member of Q.
By mathematical induction
, a set Q is convex if and only if every convex combination
of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v0, v1, . . . , vD} of a vector space is any weighted average
for some indexed set of non-negative real numbers {λd} satisfying the equation = 1.
The definition of a convex set implies that the intersection
of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set.
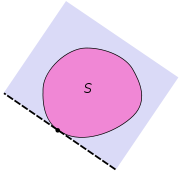Supporting hyperplane is a concept in geometry
. A hyperplane
divides a space into two half-space
s. A hyperplane is said to support a set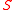
in Euclidean space
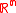if it meets both of the following:
Here, a closed half-space is the half-space that includes the hyperplane.
This theorem
states that if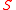
is a closed convex set
in Euclidean space
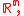and 
is a point on the boundary
of
then there exists a supporting hyperplane containing 
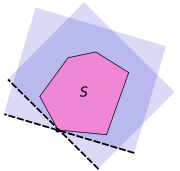
The hyperplane in the theorem may not be unique, as noticed in the second picture on the right. If the closed set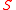
is not convex, the statement of the theorem is not true at all points on the boundary of 
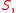as illustrated in the third picture on the right.
is supported
by the budget constraint, as shown in the diagram. If the preference set is convex, then the consumer's set of optimal decisions is a convex set, for example, a unique optimal basket (or even a line-segment of optimal baskets).
For simplicity, we shall assume that the preferences of a consumer can be described by a utility function that is a continuous function
, which implies that the preference set
s are closed
. (The meanings of "closed set" is explained below, in the subsection on optimization applications.)
)! Thus, the contemporary zoo-keeper's preferences are non-convex: The zoo-keeper prefers having either animal to having any strictly convex combination of both.
Non-convex sets have been incorporated in the theories of general economic equilibria, of market failure
s, and of public economics. These results are described in graduate-level textbooks in microeconomics
, general equilibrium theory, game theory
, mathematical economics
,
and applied mathematics (for economists). The Shapley–Folkman lemma
results establish that non-convexities are compatible with approximate equilibria in markets with many consumers; these results also apply to production economies
with many small firm
s.
In "oligopolies
" (markets dominated by a few producers), especially in "monopolies
" (markets dominated by one producer), non-convexities remain important. Concerns with large producers exploiting market power in fact initiated the literature on non-convex sets, when Piero Sraffa
wrote about on firms with increasing returns to scale
in 1926, after which Harold Hotelling
wrote about marginal cost pricing in 1938. Both Sraffa and Hotelling illuminated the market power
of producers without competitors, clearly stimulating a literature on the supply-side of the economy.
Non-convex sets arise also with environmental goods
(and other externalities
), with information economics
, and with stock market
s (and other incomplete markets
). Such applications continued to motivate economists to study non-convex sets.
, which generalizes convex analysis. "Non-convexities in [both] production and consumption ... required mathematical tools that went beyond convexity, and further development had to await the invention of non-smooth calculus" (for example, Francis Clarke's locally Lipschitz
calculus), as described by and , according to . wrote that the "major methodological innovation in the general equilibrium analysis of firms with pricing rules" was "the introduction of the methods of non- analysis, as a [synthesis] of global analysis (differential topology) and [of] convex analysis." According to , "Non-smooth analysis extends the local approximation of manifolds by tangent planes [and extends] the analogous approximation of convex sets by tangent cones to sets" that can be non-smooth or non-convex.. Economists have also used algebraic topology
.
Arrow-Debreu model
In mathematical economics, the Arrow–Debreu model suggests that under certain economic assumptions there must be a set of prices such that aggregate supplies will equal aggregate demands for every commodity in the economy.The model is central to the theory of...
of general economic equilibrium
General equilibrium
General equilibrium theory is a branch of theoretical economics. It seeks to explain the behavior of supply, demand and prices in a whole economy with several or many interacting markets, by seeking to prove that a set of prices exists that will result in an overall equilibrium, hence general...
, agents have convex budget set
Budget set
A budget set or opportunity set includes all possible consumption bundles that someone can afford given the prices of goods and the person's income level...
s and convex preferences
Convex preferences
In economics, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes"...
: At equilibrium prices, the budget hyperplane supports
Supporting hyperplane
Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...
the best attainable indifference curve
Indifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
. The profit function
Profit (economics)
In economics, the term profit has two related but distinct meanings. Normal profit represents the total opportunity costs of a venture to an entrepreneur or investor, whilst economic profit In economics, the term profit has two related but distinct meanings. Normal profit represents the total...
is the convex conjugate
Convex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
of the cost function. Convex analysis
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
is the standard tool for analyzing textbook economics. Non-convex phenomena in economics have been studied with nonsmooth analysis, which generalizes convex analysis
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
.
Preliminaries
The economics depends upon the following definitions and results from convex geometryConvex geometry
Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...
.
Real vector spaces
A realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of two dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
s may be given a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
in which every point is identified by a list of two real numbers, called "coordinates", which are conventionally denoted by x and y. Two points in the Cartesian plane can be added coordinate-wise
- (x1, y1) + (x2, y2) = (x1+x2, y1+y2);
further, a point can be multiplied
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
by each real number λ coordinate-wise
- λ (x, y) = (λx, λy).
More generally, any real vector space of (finite) dimension D can be viewed as the set of all possible lists of D real numbers } together with two operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
s: vector addition and multiplication by a real number
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
. For finite-dimensional vector spaces, the operations of vector addition and real-number multiplication can each be defined coordinate-wise, following the example of the Cartesian plane.
Convex sets
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
if, for each pair of its points, every point on the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
that joins them is covered by the set. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent
Crescent
In art and symbolism, a crescent is generally the shape produced when a circular disk has a segment of another circle removed from its edge, so that what remains is a shape enclosed by two circular arcs of different diameters which intersect at two points .In astronomy, a crescent...
shape, is non-convex. Trivially
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
, the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is convex.
More formally, a set Q is convex if, for all points v0 and v1 in Q and for every real number λ in the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1], the point
- (1 − λ) v0 + λv1
is a member of Q.
By mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, a set Q is convex if and only if every convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v0, v1, . . . , vD} of a vector space is any weighted average
Weighted mean
The weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others...
for some indexed set of non-negative real numbers {λd} satisfying the equation = 1.
The definition of a convex set implies that the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set.
Convex hull
For every subset Q of a real vector space, its is the minimal convex set that contains Q. Thus Conv(Q) is the intersection of all the convex sets that cover Q. The convex hull of a set can be equivalently defined to be the set of all convex combinations of points in Q.Duality:Intersecting half-spaces
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. A hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
divides a space into two half-space
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
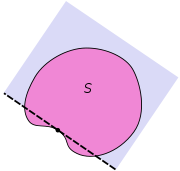
s. A hyperplane is said to support a set
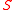in Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
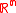if it meets both of the following:
-
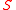is entirely contained in one of the two closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
half-spaces determined by the hyperplane -
has at least one point on the hyperplane.
Here, a closed half-space is the half-space that includes the hyperplane.
Supporting hyperplane theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
states that if
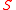is a closed convex setConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
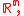and is a point on the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of
then there exists a supporting hyperplane containing The hyperplane in the theorem may not be unique, as noticed in the second picture on the right. If the closed set
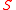is not convex, the statement of the theorem is not true at all points on the boundary of 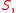as illustrated in the third picture on the right.Economics
An optimal basket of goods occurs where the consumer's convex preference setConvex preferences
In economics, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes"...
is supported
Supporting hyperplane
Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...
by the budget constraint, as shown in the diagram. If the preference set is convex, then the consumer's set of optimal decisions is a convex set, for example, a unique optimal basket (or even a line-segment of optimal baskets).
For simplicity, we shall assume that the preferences of a consumer can be described by a utility function that is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, which implies that the preference set
Convex preferences
In economics, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes"...
s are closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
. (The meanings of "closed set" is explained below, in the subsection on optimization applications.)
Non-convexity
If a preference set is non-convex, then some prices produce a budget supporting two different optimal consumption decisions. For example, we can imagine that, for zoos, a lion costs as much as an eagle, and further that a zoo's budget suffices for one eagle or one lion. We can suppose also that a zoo-keeper views either animal as equally valuable. In this case, the zoo would purchase either one lion or one eagle. Of course, a contemporary zoo-keeper does not want to purchase a half an eagle and a (or a griffinGriffin
The griffin, griffon, or gryphon is a legendary creature with the body of a lion and the head and wings of an eagle...
)! Thus, the contemporary zoo-keeper's preferences are non-convex: The zoo-keeper prefers having either animal to having any strictly convex combination of both.
Non-convex sets have been incorporated in the theories of general economic equilibria, of market failure
Market failure
Market failure is a concept within economic theory wherein the allocation of goods and services by a free market is not efficient. That is, there exists another conceivable outcome where a market participant may be made better-off without making someone else worse-off...
s, and of public economics. These results are described in graduate-level textbooks in microeconomics
Microeconomics
Microeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...
, general equilibrium theory, game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, mathematical economics
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
,
and applied mathematics (for economists). The Shapley–Folkman lemma
Shapley–Folkman lemma
In geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
results establish that non-convexities are compatible with approximate equilibria in markets with many consumers; these results also apply to production economies
Production (economics)
In economics, production is the act of creating 'use' value or 'utility' that can satisfy a want or need. The act may or may not include factors of production other than labor...
with many small firm
Business
A business is an organization engaged in the trade of goods, services, or both to consumers. Businesses are predominant in capitalist economies, where most of them are privately owned and administered to earn profit to increase the wealth of their owners. Businesses may also be not-for-profit...
s.
In "oligopolies
Oligopoly
An oligopoly is a market form in which a market or industry is dominated by a small number of sellers . The word is derived, by analogy with "monopoly", from the Greek ὀλίγοι "few" + πόλειν "to sell". Because there are few sellers, each oligopolist is likely to be aware of the actions of the others...
" (markets dominated by a few producers), especially in "monopolies
Monopoly
A monopoly exists when a specific person or enterprise is the only supplier of a particular commodity...
" (markets dominated by one producer), non-convexities remain important. Concerns with large producers exploiting market power in fact initiated the literature on non-convex sets, when Piero Sraffa
Piero Sraffa
Piero Sraffa was an influential Italian economist whose book Production of Commodities by Means of Commodities is taken as founding the Neo-Ricardian school of Economics.- Early life :...
wrote about on firms with increasing returns to scale
Returns to scale
In economics, returns to scale and economies of scale are related terms that describe what happens as the scale of production increases in the long run, when all input levels including physical capital usage are variable...
in 1926, after which Harold Hotelling
Harold Hotelling
Harold Hotelling was a mathematical statistician and an influential economic theorist.He was Associate Professor of Mathematics at Stanford University from 1927 until 1931, a member of the faculty of Columbia University from 1931 until 1946, and a Professor of Mathematical Statistics at the...
wrote about marginal cost pricing in 1938. Both Sraffa and Hotelling illuminated the market power
Market power
In economics, market power is the ability of a firm to alter the market price of a good or service. In perfectly competitive markets, market participants have no market power. A firm with market power can raise prices without losing its customers to competitors...
of producers without competitors, clearly stimulating a literature on the supply-side of the economy.
Non-convex sets arise also with environmental goods
Environmental economics
Environmental economics is a subfield of economics concerned with environmental issues. Quoting from the National Bureau of Economic Research Environmental Economics program:...
(and other externalities
Externality
In economics, an externality is a cost or benefit, not transmitted through prices, incurred by a party who did not agree to the action causing the cost or benefit...
), with information economics
Information economics
Information economics or the economics of informationis a branch of microeconomic theory that studies how information affects an economy and economic decisions. Information has special characteristics. It is easy to create but hard to trust. It is easy to spread but hard to control. It...
, and with stock market
Stock market
A stock market or equity market is a public entity for the trading of company stock and derivatives at an agreed price; these are securities listed on a stock exchange as well as those only traded privately.The size of the world stock market was estimated at about $36.6 trillion...
s (and other incomplete markets
Incomplete markets
In economics, incomplete markets refers to markets in which the number of Arrow–Debreu securities is less than the number of states of nature...
). Such applications continued to motivate economists to study non-convex sets.
Nonsmooth analysis
Economists have increasingly studied non-convex sets with nonsmooth analysisSubderivative
In mathematics, the concepts of subderivative, subgradient, and subdifferential arise in convex analysis, that is, in the study of convex functions, often in connection to convex optimization....
, which generalizes convex analysis. "Non-convexities in [both] production and consumption ... required mathematical tools that went beyond convexity, and further development had to await the invention of non-smooth calculus" (for example, Francis Clarke's locally Lipschitz
Rademacher's theorem
In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn andis Lipschitz continuous, then f is Fréchet-differentiable almost everywhere in U In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the...
calculus), as described by and , according to . wrote that the "major methodological innovation in the general equilibrium analysis of firms with pricing rules" was "the introduction of the methods of non- analysis, as a [synthesis] of global analysis (differential topology) and [of] convex analysis." According to , "Non-smooth analysis extends the local approximation of manifolds by tangent planes [and extends] the analogous approximation of convex sets by tangent cones to sets" that can be non-smooth or non-convex.. Economists have also used algebraic topology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
.