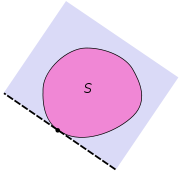
Supporting hyperplane is a concept in geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

. A hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

 divides a space into two half-space

Half-space

In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...

s. A hyperplane is said to support a set  in Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

  if it meets both of the following:

• is entirely contained in one of the two closed
  Closed set
  In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
  
   half-spaces determined by the hyperplane
• has at least one point on the hyperplane.

Here, a closed half-space is the half-space that includes the hyperplane.

Supporting hyperplane theorem

This theorem

Theorem

In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...

 states that if is a closed

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

 convex set

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 in a topological

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

  and is a point on the boundary

Boundary (topology)

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...

 of then there exists a supporting hyperplane containing If (the dual space

Dual space

In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

 of X) such that for all , then
defines a supporting hyperplane.

Conversely, if is a closed set

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

 with nonempty interior

Interior (topology)

In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....

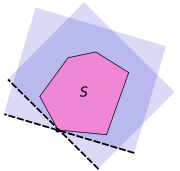
 such that every point has a supporting hyperplane, then is a convex set.

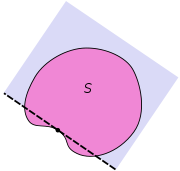
The hyperplane in the theorem may not be unique, as noticed in the second picture on the right. If the closed set is not convex, the statement of the theorem is not true at all points on the boundary of as illustrated in the third picture on the right.

A related result is the separating hyperplane theorem.

See also

• Supporting functional
  Supporting functional
  In convex analysis and mathematical optimization, the supporting functional is a generalization of the supporting hyperplane of a set.- Mathematical definition :...