Partition problem
Encyclopedia
In computer science
, the partition problem is an NP-complete
problem. The problem is to decide whether a given multiset
of integers can be partitioned
into two "halves" that have the same sum. More precisely, given a multiset S of integers, is there a way to partition S into two subsets S1 and S2 such that the sum of the numbers in S1 equals the sum of the numbers in S2? The subsets S1 and S2 must form a partition
in the sense that they are disjoint and they cover
S. The optimization version
asks for the "best" partition, and can be stated as: Find a partition into two subsets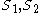
such that 
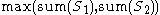(or, equivalently, the difference between 
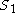and 
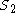) is minimized (sometimes with the additional constraint that the sizes of the two sets in the partition must be equal, or differ by at most 1).
The partition problem is equivalent to the following special case of the subset sum problem: given a set S of integers, is there a subset S1 of S that sums to exactly t /2 where t is the sum of all elements of S? (The equivalence can be seen by defining S2 to be the difference S − S1.) Therefore, the pseudo-polynomial time
dynamic programming solution to subset sum applies to the partition problem as well.
A variation of the partition problem is the 3-partition problem
, in which the set S must be partitioned into |S|/3 triples each with the same sum. In contrast to partition, 3-partition has no pseudo-polynomial time algorithm unless P = NP: 3-partition remains NP-complete even when using unary coding
.
.
The pseudo-polynomial time
dynamic programming
solution for the subset sum problem applies to the partition problem as well, and gives an exact answer in polynomial time when the size of the given integers is bounded. In general, however, the numbers in the input may be exponential in the input size, and this approach may not be feasible.
One approach to the problem, imitating the way children choose teams for a game, is the greedy algorithm, which goes through the numbers in descending order, assigning each of them to whichever subset has the smaller sum. This works well when the numbers in the set are of about the same size as its cardinality or less. Another heuristic, due to Narendra Karmarkar
and Richard Karp
, is the differencing algorithm, which at each step removes two numbers from the set and replaces them by their difference. This represents the decision to put the two numbers in different sets, without immediately deciding which one is in which set. The differencing heuristic performs better than the greedy one, but is still bad for instances where the numbers are exponential in the size of the set.
Both heuristics have a running time
of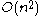
or less. The greedy algorithm is known to give a 4/3-approximation
to the optimal solution of the optimization version. (In other words, if the greedy algorithm gives two sets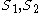
, then 
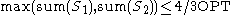.) More generally, we can consider a version that takes the 
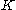largest elements, and for each partition of them, extends the partition by adding the remaining elements successively to whichever set is smaller. (The greedy algorithm corresponds to 
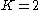.) This version runs in time 
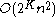and is known to give a 
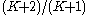approximation; thus we have a polynomial-time approximation scheme
(PTAS) for the number partition problem, though this is not an FPTAS (the running time is exponential in the desired approximation guarantee). However, there are variations of this idea that are fully polynomial-time approximation schemes for the subset-sum problem, and hence for the partition problem as well. On the other hand, the problem of minimizing the square of the difference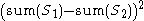
has no FPTAS unless P=NP.
There are also anytime algorithm
s, based on the differencing heuristic, that first find the solution returned by the differencing heuristic, then find progressively better solutions as time allows (possibly requiring exponential time to reach optimality, for the worst instances).
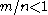tends to have many solutions and 
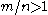tends to have few or no solutions. As n and m get larger, the probability of a perfect partition goes to 1 or 0 respectively. This was originally argued using methods from physics by Stephan Mertens, and later proved by Borgs, Chayes
, and Pittel.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the partition problem is an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem. The problem is to decide whether a given multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of integers can be partitioned
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
into two "halves" that have the same sum. More precisely, given a multiset S of integers, is there a way to partition S into two subsets S1 and S2 such that the sum of the numbers in S1 equals the sum of the numbers in S2? The subsets S1 and S2 must form a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
in the sense that they are disjoint and they cover
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
S. The optimization version
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
asks for the "best" partition, and can be stated as: Find a partition into two subsets
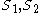such that 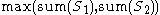(or, equivalently, the difference between 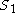and 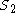) is minimized (sometimes with the additional constraint that the sizes of the two sets in the partition must be equal, or differ by at most 1).The partition problem is equivalent to the following special case of the subset sum problem: given a set S of integers, is there a subset S1 of S that sums to exactly t /2 where t is the sum of all elements of S? (The equivalence can be seen by defining S2 to be the difference S − S1.) Therefore, the pseudo-polynomial time
Pseudo-polynomial time
In computational complexity theory, a numeric algorithm runs in pseudo-polynomial time if its running time is polynomial in the numeric value of the input ....
dynamic programming solution to subset sum applies to the partition problem as well.
A variation of the partition problem is the 3-partition problem
3-partition problem
The 3-partition problem is an NP-complete problem in computer science. The problem is to decide whether a given multiset of integers can be partitioned into triples that all have the same sum...
, in which the set S must be partitioned into |S|/3 triples each with the same sum. In contrast to partition, 3-partition has no pseudo-polynomial time algorithm unless P = NP: 3-partition remains NP-complete even when using unary coding
Unary coding
Unary coding, sometimes called thermometer code, is an entropy encoding that represents a natural number, n, with n ones followed by a zero or with n − 1 ones followed by a zero...
.
Methods
Although the partition problem is NP-complete, there are heuristics that solve the problem in many instances, either optimally or approximately. For this reason, it has been called "The Easiest Hard Problem" by Brian HayesBrian Hayes (scientist)
Brian Hayes is an American scientist, columnist and author.He is a senior writer and regular columnist for the magazine American Scientist, and was editor in chief for the magazine from 1990 to 1992. He has also edited and written columns for Scientific American, as well as writing for Computer...
.
The pseudo-polynomial time
Pseudo-polynomial time
In computational complexity theory, a numeric algorithm runs in pseudo-polynomial time if its running time is polynomial in the numeric value of the input ....
dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
solution for the subset sum problem applies to the partition problem as well, and gives an exact answer in polynomial time when the size of the given integers is bounded. In general, however, the numbers in the input may be exponential in the input size, and this approach may not be feasible.
One approach to the problem, imitating the way children choose teams for a game, is the greedy algorithm, which goes through the numbers in descending order, assigning each of them to whichever subset has the smaller sum. This works well when the numbers in the set are of about the same size as its cardinality or less. Another heuristic, due to Narendra Karmarkar
Narendra Karmarkar
Narendra K. Karmarkar is an Indian mathematician, renowned for developing Karmarkar's algorithm. He is listed as an ISI highly cited researcher.- Biography :...
and Richard Karp
Richard Karp
Richard Manning Karp is a computer scientist and computational theorist at the University of California, Berkeley, notable for research in the theory of algorithms, for which he received a Turing Award in 1985, The Benjamin Franklin Medal in Computer and Cognitive Science in 2004, and the Kyoto...
, is the differencing algorithm, which at each step removes two numbers from the set and replaces them by their difference. This represents the decision to put the two numbers in different sets, without immediately deciding which one is in which set. The differencing heuristic performs better than the greedy one, but is still bad for instances where the numbers are exponential in the size of the set.
Both heuristics have a running time
Running Time
Running Time may refer to:* Running Time * see Analysis of algorithms...
of
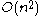or less. The greedy algorithm is known to give a 4/3-approximationApproximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
to the optimal solution of the optimization version. (In other words, if the greedy algorithm gives two sets
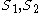, then 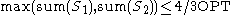.) More generally, we can consider a version that takes the 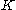largest elements, and for each partition of them, extends the partition by adding the remaining elements successively to whichever set is smaller. (The greedy algorithm corresponds to 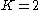.) This version runs in time 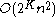and is known to give a 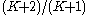approximation; thus we have a polynomial-time approximation schemePolynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
(PTAS) for the number partition problem, though this is not an FPTAS (the running time is exponential in the desired approximation guarantee). However, there are variations of this idea that are fully polynomial-time approximation schemes for the subset-sum problem, and hence for the partition problem as well. On the other hand, the problem of minimizing the square of the difference
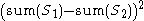has no FPTAS unless P=NP.There are also anytime algorithm
Anytime algorithm
In computer science an anytime algorithm is an algorithm that can return a valid solution to a problem even if it's interrupted at any time before it ends. The algorithm is expected to find better and better solutions the more time it keeps running....
s, based on the differencing heuristic, that first find the solution returned by the differencing heuristic, then find progressively better solutions as time allows (possibly requiring exponential time to reach optimality, for the worst instances).
Hard instances
Sets with 1 or no partitions tend to be hardest (or most expensive) to solve compared to their input sizes. When the values are small compared to the size of the set, perfect partitions are more likely. The problem is known to undergo a "phase transition"; being likely for some sets and unlikely for others. If m is the number of bits needed to express any number in the set and n is the size of the set then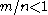 tends to have many solutions and 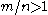tends to have few or no solutions. As n and m get larger, the probability of a perfect partition goes to 1 or 0 respectively. This was originally argued using methods from physics by Stephan Mertens, and later proved by Borgs, ChayesJennifer Tour Chayes
Jennifer Tour Chayes is Managing Director and Distinguished Scientist of Microsoft Research New England Lab in Cambridge, Massachusetts, which she co-founded in July 2008. She received her Ph.D. in mathematical physics at Princeton University...
, and Pittel.