Pseudo-polynomial time
Encyclopedia
In computational complexity theory
, a numeric algorithm runs in pseudo-polynomial time if its running time is polynomial
in the numeric value of the input (which is exponential in the length of the input – its number of digits).
An NP-complete
problem with known pseudo-polynomial time algorithms is called weakly NP-complete
.
An NP-complete
problem is called strongly NP-complete
if it is proven that it cannot be solved by a pseudo-polynomial time algorithm unless P=NP. The strong/weak kinds of NP-hard
ness are defined analogously.
, by naively checking whether no number in {2, 3, ...,
} divides n evenly. This approach can take up to divisions, which is sub-linear in the value of n but exponential in the size of n (which is about 
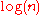). For example, the number would require at most approximately 100,000 divisions, even though the length of n is only 11 digits. Moreover one can easily write down an input (say, a 300-digit number) for which this algorithm is impractical. Since computational complexity measures difficulty with respect to the length of the (encoded) input, this naive algorithm is actually exponential. It is, however, pseudo-polynomial time.
Contrast this algorithm with a true polynomial numeric algorithm -- say, the straightforward algorithm for addition: Adding two 9-digit numbers takes around 9 simple steps, and in general the algorithm is truly linear in the length of the input. Compared with the actual numbers being added (in the billions), the algorithm could be called "pseudo-logarithmic time", though such a term is not standard. Thus, adding 300-digit numbers is not impractical. Similarly, long division is quadratic: an m-digit number can be divided by a n-digit number in
steps (see Big O notation
.)
In the case of primality, it turns out there is a different algorithm for testing whether n is prime
(discovered in 2002) which runs in time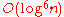
.
Another example of a problem which can be generally only solved in pseudo-polynomial time is the Knapsack problem
.
The function m is pseudo-polynomial if
m(n) is no greater than a polynomial function of the problem size n and an additional property of the input, k(n). (Presumably, k is chosen to be something relevant to the problem.)
This makes numeric problems a special case by taking k to be the number of (binary) digits of the input.
The distinction between the value of a number and its length is one of encoding: if numeric inputs are always encoded in unary
, then pseudo-polynomial would coincide with polynomial.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, a numeric algorithm runs in pseudo-polynomial time if its running time is polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in the numeric value of the input (which is exponential in the length of the input – its number of digits).
An NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem with known pseudo-polynomial time algorithms is called weakly NP-complete
Weakly NP-complete
In computational complexity, an NP-complete problem is weakly NP-complete , if there is an algorithm for the problem whose running time is polynomial in the dimension of the problem and the magnitudes of the data involved , rather than the base-two logarithms of their magnitudes...
.
An NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem is called strongly NP-complete
Strongly NP-complete
In computational complexity, strong NP-completeness is a property of computational problems that is a special case of NP-completeness. A general computational problem may have numerical parameters...
if it is proven that it cannot be solved by a pseudo-polynomial time algorithm unless P=NP. The strong/weak kinds of NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
ness are defined analogously.
Example
Consider the problem of testing whether a number n is primePrimality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
, by naively checking whether no number in {2, 3, ...,
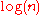} divides n evenly. This approach can take up to divisions, which is sub-linear in the value of n but exponential in the size of n (which is about ). For example, the number would require at most approximately 100,000 divisions, even though the length of n is only 11 digits. Moreover one can easily write down an input (say, a 300-digit number) for which this algorithm is impractical. Since computational complexity measures difficulty with respect to the length of the (encoded) input, this naive algorithm is actually exponential. It is, however, pseudo-polynomial time.Contrast this algorithm with a true polynomial numeric algorithm -- say, the straightforward algorithm for addition: Adding two 9-digit numbers takes around 9 simple steps, and in general the algorithm is truly linear in the length of the input. Compared with the actual numbers being added (in the billions), the algorithm could be called "pseudo-logarithmic time", though such a term is not standard. Thus, adding 300-digit numbers is not impractical. Similarly, long division is quadratic: an m-digit number can be divided by a n-digit number in
steps (see Big O notationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
.)
In the case of primality, it turns out there is a different algorithm for testing whether n is prime
AKS primality test
The AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...
(discovered in 2002) which runs in time
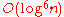.Another example of a problem which can be generally only solved in pseudo-polynomial time is the Knapsack problem
Knapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
.
Generalizing to non-numeric problems
Although the notion of pseudo-polynomial time is used almost exclusively for numeric problems, the concept can be generalized:The function m is pseudo-polynomial if
m(n) is no greater than a polynomial function of the problem size n and an additional property of the input, k(n). (Presumably, k is chosen to be something relevant to the problem.)
This makes numeric problems a special case by taking k to be the number of (binary) digits of the input.
The distinction between the value of a number and its length is one of encoding: if numeric inputs are always encoded in unary
Unary numeral system
The unary numeral system is the bijective base-1 numeral system. It is the simplest numeral system to represent natural numbers: in order to represent a number N, an arbitrarily chosen symbol representing 1 is repeated N times. For example, using the symbol | , the number 6 is represented as ||||||...
, then pseudo-polynomial would coincide with polynomial.