Primality test
Encyclopedia
A primality test is an algorithm
for determining whether an input number is prime
. Amongst other fields of mathematics
, it is used for cryptography
. Unlike integer factorization
, primality tests do not generally give prime factor
s, only stating whether the input number is prime or not. , factorization is a computationally difficult problem, whereas primality testing is comparatively easy (its running time is polynomial in the size of the input). Some primality tests prove that a number is prime, while others like Miller-Rabin prove that a number is composite
. Therefore we might call the latter compositeness tests instead of primality tests.
check whether any integer m from 2 to n − 1 divides n. If n is divisible by any m then n is composite, otherwise it is prime.
However, rather than testing all m up to n − 1, it is only necessary to test m up to
: if n is composite then it can be factored into two values, at least one of which must be less than or equal to 
.
The efficiency can also be improved by skipping all even m except 2, since if any even number divides n then 2 does. It can be improved further by observing that all primes are of the form 6k ± 1, with 2 and 3 being the only exceptions. This is because all integers can be expressed as (6k + i) for some integer k and for i = −1, 0, 1, 2, 3, or 4; 2 divides (6k + 0), (6k + 2), (6k + 4); and 3 divides (6k + 3). So a more efficient method is to test if n is divisible by 2 or 3, then to check through all the numbers of form 6k ± 1
. This is 3 times as fast as testing all m.
Generalising further, it can be seen that all primes are of the form c#k + i for i < c# where i represents the numbers that are coprime
to c#
and where c and k are integers. For example, let c = 6. Then c# = 2
3 
5 = 30. All integers are of the form 30k + i for i = 0, 1, 2,...,29 and k an integer. However, 2 divides 0, 2, 4,...,28 and 3 divides 0, 3, 6,...,27 and 5 divides 0, 5, 10,...,25. So all prime numbers are of the form 30k + i for i = 1, 7, 11, 13, 17, 19, 23, 29 (i.e. for i < 30 such that gcd
(i,30) = 1). Note that if i and 30 are not coprime, then 30k + i is divisible by a prime divisor of 30, namely 2, 3 or 5, and is therefore not prime.
As c → ∞, the number of values that c#k + i can take over a certain range decreases, and so the time to test n decreases. For this method, it is also necessary to check for divisibility by all primes that are less than c. Observations analogous to the preceding can be applied recursively
, giving the Sieve of Eratosthenes
.
A good way to speed up these methods (and all the others mentioned below) is to pre-compute and store a list of all primes up to a certain bound, say all primes up to 200. (Such a list can be computed with the Sieve of Eratosthenes). Then, before testing n for primality with a serious method, n can first be checked for divisibility by any prime from the list. If it is divisible by any of those numbers then it is composite, and any further tests can be skipped.
A simple, but very inefficient primality test uses Wilson's theorem, which states that p is prime if and only if:
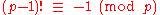
Although this method requires about p modular multiplications, rendering it impractical, theorems about primes and modular residues form the basis of many more practical methods.
. These tests use, apart from the tested number n, some other numbers a which are chosen at random from some sample space; the usual randomized primality tests never report a prime number as composite, but it is possible for a composite number to be reported as prime. The probability of error can be reduced by repeating the test with several independently chosen values of a; for two commonly used tests, for any composite n at least half the as detect ns compositeness, so k repetitions reduce the error probability to at most 2−k, which can be made arbitrarily small by increasing k.
The basic structure of randomized primality tests is as follows:
After several iterations, if n is not found to be a composite number, then it can be declared probably prime
.
The simplest probabilistic primality test is the Fermat primality test
(actually a compositeness test). It works as follows:
The Fermat primality test is only a heuristic test; some composite numbers (Carmichael numbers) will be declared "probably prime" no matter what witness is chosen. Nevertheless, it is often used if a rapid screening of numbers is needed, for instance in the key generation phase of the RSA public key cryptographic algorithm.
The Miller–Rabin primality test and Solovay–Strassen primality test are more sophisticated variants which detect all composites (once again, this means: for every composite number n, at least 3/4 (Miller–Rabin) or 1/2 (Solovay–Strassen) of numbers a are witnesses of compositeness of n). These are also compositeness tests.
The Miller–Rabin primality test works as follows:
Given an integer n, choose some integer a < n. Let 2sd = n − 1 where d is odd. If
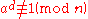
and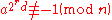
for all 
then n is composite and a is a witness for the compositeness. Otherwise, n may or may not be prime.
The Solovay–Strassen primality test uses another equality: Given an odd number n, choose some integer a < n, if
, where 
is the Jacobi symbol
,
then n is composite and a is a witness for the compositeness. Otherwise, n may or may not be prime.
These two primality tests are often the methods of choice, as they are simple and much faster than other general primality tests. One method of improving efficiency further in some cases is the Frobenius pseudoprimality test
; a round of this test takes about three times as long as a round of Miller–Rabin, but achieves a probability bound comparable to seven rounds of Miller–Rabin.
Leonard Adleman
and Huang presented an errorless (but expected polynomial-time) variant of the elliptic curve primality test
. Unlike the other probabilistic tests, this algorithm produces a primality certificate
, and thus can be used to prove that a number is prime. The algorithm is prohibitively slow in practice.
could be used to test for primality. This resulted in the Pocklington primality test
. However, as this test requires a partial factorization of n − 1 the running time was still quite slow in the worst case. The first deterministic
primality test significantly faster than the naïve methods was the cyclotomy test; its runtime can be proven to be O
((log n)clog log log n), where n is the number to test for primality and c is a constant independent of n. Many further improvements were made, but none could be proven to have polynomial running time. (Note that running time is measured in terms of the size of the input, which in this case is ~ log n, that being the number of bits needed to represent the number n.) The elliptic curve primality test
can be proven to run in O((log n)6), but only if some still unproven (but widely assumed to be true) statements of analytic number theory
are used. Similarly, under the generalized Riemann hypothesis
, the Miller–Rabin test can be turned into a deterministic version (called Miller's test) with runtime Õ((log n)4). In practice, this algorithm is slower than the other two for sizes of numbers that can be dealt with at all. Because the implementation of these methods is rather difficult and creates a risk of programming errors, the slower but simpler tests are often preferred.
In 2002 the first provably polynomial time test for primality was invented by Manindra Agrawal
, Neeraj Kayal
and Nitin Saxena
. The AKS primality test
, runs in Õ((log n)12) (improved to Õ((log n)7.5) in the published revision of their paper), which can be further reduced to Õ((log n)6) if the Sophie Germain conjecture
is true. Subsequently, Lenstra and Pomerance presented a version of the test which runs in time Õ((log n)6) unconditionally.
, the formal language corresponding to the prime numbers is denoted as PRIMES. It is easy to show that PRIMES is in Co-NP: its complement COMPOSITES is in NP because one can decide compositeness by nondeterministically guessing a factor.
In 1975, Vaughan Pratt showed that there existed a certificate for primality that was checkable in polynomial time, and thus that PRIMES was in NP
, and therefore in NP ∩ coNP. See primality certificate
for details.
The subsequent discovery of the Solovay-Strassen and Miller-Rabin algorithms put PRIMES in coRP
. In 1992, the Adleman-Huang algorithm reduced the complexity to ZPP = RP ∩ coRP, which superseded Pratt's result.
The cyclotomy test of Adleman, Pomerance
, and Rumely from 1983 put PRIMES in QP (quasi-polynomial time), which is not known to be comparable with the classes mentioned above.
Because of its tractability in practice, polynomial-time algorithms assuming the Riemann hypothesis, and other similar evidence, it was long suspected but not proven that primality could be solved in polynomial time. The existence of the AKS primality test
finally settled this long-standing question and placed PRIMES in P
. However, PRIMES is not known to be P-complete
, and it is not known whether it lies in classes lying inside P such as NC
or L
.
. These tests typically require factorization of n + 1, n − 1, or a similar quantity, which means that they are not useful for general-purpose primality testing, but they are often quite powerful when the tested number n is known to have a special form.
The Lucas test relies on the fact that the multiplicative order
of a number a modulo n is n − 1 for a prime n when a is a primitive root modulo n
. If we can show a is primitive for n, we can show n is prime.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for determining whether an input number is prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. Amongst other fields of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, it is used for cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
. Unlike integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
, primality tests do not generally give prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s, only stating whether the input number is prime or not. , factorization is a computationally difficult problem, whereas primality testing is comparatively easy (its running time is polynomial in the size of the input). Some primality tests prove that a number is prime, while others like Miller-Rabin prove that a number is composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
. Therefore we might call the latter compositeness tests instead of primality tests.
Naive methods
The simplest primality test is as follows: Given an input number n,check whether any integer m from 2 to n − 1 divides n. If n is divisible by any m then n is composite, otherwise it is prime.
However, rather than testing all m up to n − 1, it is only necessary to test m up to
: if n is composite then it can be factored into two values, at least one of which must be less than or equal to .The efficiency can also be improved by skipping all even m except 2, since if any even number divides n then 2 does. It can be improved further by observing that all primes are of the form 6k ± 1, with 2 and 3 being the only exceptions. This is because all integers can be expressed as (6k + i) for some integer k and for i = −1, 0, 1, 2, 3, or 4; 2 divides (6k + 0), (6k + 2), (6k + 4); and 3 divides (6k + 3). So a more efficient method is to test if n is divisible by 2 or 3, then to check through all the numbers of form 6k ± 1
. This is 3 times as fast as testing all m.Generalising further, it can be seen that all primes are of the form c#k + i for i < c# where i represents the numbers that are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to c#
Primorial
In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
and where c and k are integers. For example, let c = 6. Then c# = 2
3 5 = 30. All integers are of the form 30k + i for i = 0, 1, 2,...,29 and k an integer. However, 2 divides 0, 2, 4,...,28 and 3 divides 0, 3, 6,...,27 and 5 divides 0, 5, 10,...,25. So all prime numbers are of the form 30k + i for i = 1, 7, 11, 13, 17, 19, 23, 29 (i.e. for i < 30 such that gcdGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(i,30) = 1). Note that if i and 30 are not coprime, then 30k + i is divisible by a prime divisor of 30, namely 2, 3 or 5, and is therefore not prime.
As c → ∞, the number of values that c#k + i can take over a certain range decreases, and so the time to test n decreases. For this method, it is also necessary to check for divisibility by all primes that are less than c. Observations analogous to the preceding can be applied recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
, giving the Sieve of Eratosthenes
Sieve of Eratosthenes
In mathematics, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to a specified integer....
.
A good way to speed up these methods (and all the others mentioned below) is to pre-compute and store a list of all primes up to a certain bound, say all primes up to 200. (Such a list can be computed with the Sieve of Eratosthenes). Then, before testing n for primality with a serious method, n can first be checked for divisibility by any prime from the list. If it is divisible by any of those numbers then it is composite, and any further tests can be skipped.
A simple, but very inefficient primality test uses Wilson's theorem, which states that p is prime if and only if:
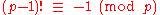
Although this method requires about p modular multiplications, rendering it impractical, theorems about primes and modular residues form the basis of many more practical methods.
Probabilistic tests
Most popular primality tests are probabilistic testsRandomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
. These tests use, apart from the tested number n, some other numbers a which are chosen at random from some sample space; the usual randomized primality tests never report a prime number as composite, but it is possible for a composite number to be reported as prime. The probability of error can be reduced by repeating the test with several independently chosen values of a; for two commonly used tests, for any composite n at least half the as detect ns compositeness, so k repetitions reduce the error probability to at most 2−k, which can be made arbitrarily small by increasing k.
The basic structure of randomized primality tests is as follows:
- Randomly pick a number a.
- Check some equality (corresponding to the chosen test) involving a and the given number n. If the equality fails to hold true, then n is a composite number, a is known as a witness for the compositeness, and the test stops.
- Repeat from step 1 until the required certainty is achieved.
After several iterations, if n is not found to be a composite number, then it can be declared probably prime
Probable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
.
The simplest probabilistic primality test is the Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
(actually a compositeness test). It works as follows:
- Given an integer n, choose some integer a coprime to n and calculate an − 1 moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n. If the result is different from 1, then n is composite. If it is 1, then n may or may not be prime.
The Fermat primality test is only a heuristic test; some composite numbers (Carmichael numbers) will be declared "probably prime" no matter what witness is chosen. Nevertheless, it is often used if a rapid screening of numbers is needed, for instance in the key generation phase of the RSA public key cryptographic algorithm.
The Miller–Rabin primality test and Solovay–Strassen primality test are more sophisticated variants which detect all composites (once again, this means: for every composite number n, at least 3/4 (Miller–Rabin) or 1/2 (Solovay–Strassen) of numbers a are witnesses of compositeness of n). These are also compositeness tests.
The Miller–Rabin primality test works as follows:
Given an integer n, choose some integer a < n. Let 2sd = n − 1 where d is odd. If
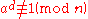
and
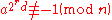for all then n is composite and a is a witness for the compositeness. Otherwise, n may or may not be prime.
The Solovay–Strassen primality test uses another equality: Given an odd number n, choose some integer a < n, if
, where is the Jacobi symbolJacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
,
then n is composite and a is a witness for the compositeness. Otherwise, n may or may not be prime.
These two primality tests are often the methods of choice, as they are simple and much faster than other general primality tests. One method of improving efficiency further in some cases is the Frobenius pseudoprimality test
Frobenius pseudoprime
In number theory, a Frobenius pseudoprime is a composite number which passes a three-step probable prime test set out by Jon Grantham in section 3 of his paper "Frobenius pseudoprimes"...
; a round of this test takes about three times as long as a round of Miller–Rabin, but achieves a probability bound comparable to seven rounds of Miller–Rabin.
Leonard Adleman
Leonard Adleman
Leonard Max Adleman is an American theoretical computer scientist and professor of computer science and molecular biology at the University of Southern California. He is known for being a co-inventor of the RSA cryptosystem in 1977, and of DNA computing...
and Huang presented an errorless (but expected polynomial-time) variant of the elliptic curve primality test
Elliptic curve primality proving
Elliptic Curve Primality Proving is a method based on elliptic curves to prove the primality of a number . It is a general-purpose algorithm, meaning it does not depend on the number being of a special form...
. Unlike the other probabilistic tests, this algorithm produces a primality certificate
Primality certificate
In mathematics and computer science, a primality certificate or primality proof is a succinct, formal proof that a number is prime. Primality certificates allow the primality of a number to be rapidly checked without having to run an expensive or unreliable primality test...
, and thus can be used to prove that a number is prime. The algorithm is prohibitively slow in practice.
Fast deterministic tests
Near the beginning of the 20th century, it was shown that a result of Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
could be used to test for primality. This resulted in the Pocklington primality test
Pocklington primality test
In mathematics, the Pocklington–Lehmer primality test is a primality test devised by Henry Cabourn Pocklington and Derrick Henry Lehmer to decide whether a given number N is prime...
. However, as this test requires a partial factorization of n − 1 the running time was still quite slow in the worst case. The first deterministic
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
primality test significantly faster than the naïve methods was the cyclotomy test; its runtime can be proven to be O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
((log n)clog log log n), where n is the number to test for primality and c is a constant independent of n. Many further improvements were made, but none could be proven to have polynomial running time. (Note that running time is measured in terms of the size of the input, which in this case is ~ log n, that being the number of bits needed to represent the number n.) The elliptic curve primality test
Elliptic curve primality proving
Elliptic Curve Primality Proving is a method based on elliptic curves to prove the primality of a number . It is a general-purpose algorithm, meaning it does not depend on the number being of a special form...
can be proven to run in O((log n)6), but only if some still unproven (but widely assumed to be true) statements of analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
are used. Similarly, under the generalized Riemann hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
, the Miller–Rabin test can be turned into a deterministic version (called Miller's test) with runtime Õ((log n)4). In practice, this algorithm is slower than the other two for sizes of numbers that can be dealt with at all. Because the implementation of these methods is rather difficult and creates a risk of programming errors, the slower but simpler tests are often preferred.
In 2002 the first provably polynomial time test for primality was invented by Manindra Agrawal
Manindra Agrawal
Manindra Agrawal is a professor at the department of computer science and engineering and the Dean of Resource, Planning and Generation at the Indian Institute of Technology, Kanpur. He is also the recipient of the first Infosys Prize for Mathematics.-Early life:Manindra Agrawal obtained a...
, Neeraj Kayal
Neeraj Kayal
Neeraj Kayal is an Indian computer scientist. Kayal was born and raised in Guwahati, India.Kayal graduated with a B.Tech from the Computer Science Department of the Indian Institute of Technology, Kanpur , India in 2002...
and Nitin Saxena
Nitin Saxena
Nitin Saxena is an Indian scientist, active in the fields of mathematics and theoretical computer science. His research focuses on topics in computational complexity, especially algebraic approaches....
. The AKS primality test
AKS primality test
The AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...
, runs in Õ((log n)12) (improved to Õ((log n)7.5) in the published revision of their paper), which can be further reduced to Õ((log n)6) if the Sophie Germain conjecture
Sophie Germain prime
In number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. For example, 23 is a Sophie Germain prime because it is a prime and 2 × 23 + 1 = 47, and 47 is also a prime number...
is true. Subsequently, Lenstra and Pomerance presented a version of the test which runs in time Õ((log n)6) unconditionally.
Complexity
In computational complexity theoryComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the formal language corresponding to the prime numbers is denoted as PRIMES. It is easy to show that PRIMES is in Co-NP: its complement COMPOSITES is in NP because one can decide compositeness by nondeterministically guessing a factor.
In 1975, Vaughan Pratt showed that there existed a certificate for primality that was checkable in polynomial time, and thus that PRIMES was in NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, and therefore in NP ∩ coNP. See primality certificate
Primality certificate
In mathematics and computer science, a primality certificate or primality proof is a succinct, formal proof that a number is prime. Primality certificates allow the primality of a number to be rapidly checked without having to run an expensive or unreliable primality test...
for details.
The subsequent discovery of the Solovay-Strassen and Miller-Rabin algorithms put PRIMES in coRP
RP (complexity)
In complexity theory, RP is the complexity class of problems for which a probabilistic Turing machine exists with these properties:* It always runs in polynomial time in the input size...
. In 1992, the Adleman-Huang algorithm reduced the complexity to ZPP = RP ∩ coRP, which superseded Pratt's result.
The cyclotomy test of Adleman, Pomerance
Carl Pomerance
Carl Bernard Pomerance is a well-known number theorist. He attended college at Brown University and later received his Ph.D. from Harvard University in 1972 with a dissertation proving that any odd perfect number has at least 7 distinct prime factors. He immediately joined the faculty at the...
, and Rumely from 1983 put PRIMES in QP (quasi-polynomial time), which is not known to be comparable with the classes mentioned above.
Because of its tractability in practice, polynomial-time algorithms assuming the Riemann hypothesis, and other similar evidence, it was long suspected but not proven that primality could be solved in polynomial time. The existence of the AKS primality test
AKS primality test
The AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...
finally settled this long-standing question and placed PRIMES in P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
. However, PRIMES is not known to be P-complete
P-complete
In complexity theory, the notion of P-complete decision problems is useful in the analysis of both:# which problems are difficult to parallelize effectively, and;# which problems are difficult to solve in limited space....
, and it is not known whether it lies in classes lying inside P such as NC
NC (complexity)
In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
or L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
.
Number-theoretic methods
Certain number-theoretic methods exist for testing whether a number is prime, such as the Lucas test and Proth's testProth's theorem
In number theory, Proth's theorem is a primality test for Proth numbers.It states that if p is a Proth number, of the form k2n + 1 with k odd and k In number theory, Proth's theorem is a primality test for Proth numbers....
. These tests typically require factorization of n + 1, n − 1, or a similar quantity, which means that they are not useful for general-purpose primality testing, but they are often quite powerful when the tested number n is known to have a special form.
The Lucas test relies on the fact that the multiplicative order
Multiplicative order
In number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
of a number a modulo n is n − 1 for a prime n when a is a primitive root modulo n
Primitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
. If we can show a is primitive for n, we can show n is prime.
External links
- Distinguishing prime numbers from composite numbers, D.J. Bernstein
- The Prime Pages
- Lucas Primality Test with Factored N-1 at MathPages
- PRIMABOINCA is a research project that uses Internet-connected computers to search for a counterexampleCounterexampleIn logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
to some conjectures. The first conjecture (Agrawal’s Conjecture) was the basis for the formulation of the first deterministic prime test algorithm in polynomial time (AKS algorithm).