In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, and more particularly in number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

, primorial is a function from natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s to natural numbers similar to the factorial

Factorial

In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...

 function, but rather than multiplying successive positive integers, only successive prime number

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

s are multiplied. There are two conflicting definitions that differ in the interpretation of the argument: the first interprets the argument as an index into the sequence of prime numbers (so that the function is strictly increasing), while the second interprets the argument as a bound on the prime numbers to be multiplied (so that the function value at any composite number is the same for its predecessor). The name "primorial", attributed to Harvey Dubner

Harvey Dubner

Harvey Dubner is a semi-retired engineer living in New Jersey, noted for his contributions to finding large prime numbers. In 1984, he and his son Robert collaborated in developing the 'Dubner cruncher', a board which used a commercial finite impulse response filter chip to speed up dramatically...

, draws an analogy to primes the same way the name "factorial" relates to factors.

Definition for prime numbers

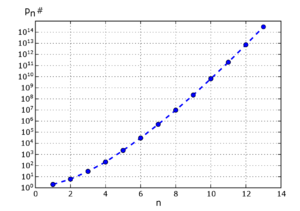
For the nth prime number p_n the primorial p_n# is defined as the product of the first n primes:


where p_k is the kth prime number.

For instance, p₅# signifies the product of the first 5 primes:


The first few primorials p_n# are:

1, 2, 6, 30

30 (number)

30 is the natural number following 29 and preceding 31.-In mathematics:30 is the sum of the first four squares, which makes it a square pyramidal number.It is a primorial and is the smallest Giuga number....

, 210

210 (number)

210 is the natural number following 209 and preceding 211.- In mathematics :210 is a composite number, an abundant number, and the product of the first four prime numbers , and thus a primorial...

, 2310.

The sequence also includes p₀# = 1 as empty product

Empty product

In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...

.

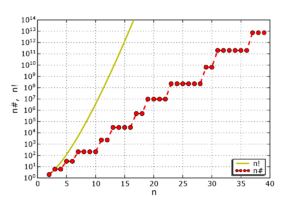
Asymptotically, primorials p_n# grow according to:


where is the little-o notation.

Definition for natural numbers

In general, for a positive integer n such a primorial n# can also be defined, namely as the product of those primes ≤ n:


where, π(n) is the prime-counting function , giving the number of primes ≤ n.

This is equivalent to:


For example, 12# represents the product of those primes ≤ 12:


Since π(12) = 5, this can be calculated as:


Consider the first 12 primorials n#:

1, 2, 6, 6, 30, 30, 210, 210, 210, 210, 2310, 2310.

We see that for composite n every term n# simply duplicates the preceding term (n−1)#, as given in the definition. In the above example we have that 12#  =  p₅#  =  11#, since 12 is a composite number.

Natural logarithm of n# is the first Chebyshev function

Chebyshev function

[Image:ChebyshevPsi.png|thumb|right|The Chebyshev function ψ, with x [Image:ChebyshevPsi.png|thumb|right|The Chebyshev function ψ, with x ...

, written or , which approaches the linear n for large n.

Primorials n# grow according to:

The idea of multiplying all known primes occurs in a proof of the infinitude of the prime numbers; it is applied to show a contradiction in the idea that the primes could be finite in number.

Applications and properties

Primorials play a role in the search for prime numbers in additive arithmetic progressions

Primes in arithmetic progression

In number theory, the phrase primes in arithmetic progression refers to at least three prime numbers that are consecutive terms in an arithmetic progression, for example the primes ....

. For instance, 2236133941 + 23# results in a prime, beginning a sequence of thirteen primes found by repeatedly adding 23#, and ending with 5136341251. 23# is also the common difference in arithmetic progressions of fifteen and sixteen primes.

Every highly composite number

Highly composite number

A highly composite number is a positive integer with more divisors than any positive integer smaller than itself.The initial or smallest twenty-one highly composite numbers are listed in the table at right....

 is a product of primorials (e.g. 360

360 (number)

360 or three sixty is the natural number following 359 and preceding 361.-In mathematics:*Divisors are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 and 360. *360 makes a highly composite number...

 = 2·6·30).

Primorials are all square-free integer

Square-free integer

In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...

s, and each one has more distinct prime factor

Prime factor

In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...

s than any number smaller than it. For each primorial n, the fraction is smaller than for any lesser integer, where is the Euler totient function.

Any completely multiplicative function

Completely multiplicative function

In number theory, functions of positive integers which respect products are important and are called completely multiplicative functions or totally multiplicative functions. Especially in number theory, a weaker condition is also important, respecting only products of coprime numbers, and such...

 is defined by its values at primorials, since it is defined by its values at primes, which can be recovered by division of adjacent values.

Primorial base systems (such as Base 30

Base 30

Base 30 or trigesimal is a positional numeral system using 30 as the radix. Digits in this base can be represented using the Arabic numerals 0-9 and the Latin letters A-T....

) are the most practical in the sense that they have the lowest proportion of recurring fractions.

Table of primorials

n	n#	pn	pn#
0	1	no prime	1
1	1	2	2
2	2	3	6
3	6	5	30
4	6	7	210
5	30	11	2310
6	30	13	30030
7	210	17	510510
8	210	19	9699690
9	210	23	223092870
10	210	29	6469693230
11	2310	31	200560490130
12	2310	37	7420738134810
13	30030	41	304250263527210
14	30030	43	13082761331670030
15	30030	47	614889782588491410
16	30030	53	32589158477190044730
17	510510	59	1922760350154212639070
18	510510	61	117288381359406970983270
19	9699690	67	7858321551080267055879090
20	9699690	71	557940830126698960967415390