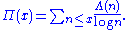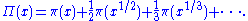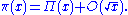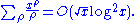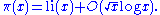Chebyshev function
Encyclopedia
In mathematics
, the Chebyshev function is either of two related functions. The first Chebyshev function ϑ(x) or θ(x) is given by
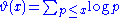
with the sum extending over all prime number
s p that are less than or equal to x.
The second Chebyshev function ψ(x) is defined similarly, with the sum extending over all prime powers not exceeding x:
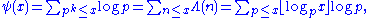
where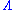
is the von Mangoldt function
. The Chebyshev function is often used in proofs related to prime numbers, because it is typically simpler to work with than the prime-counting function, π(x). Both Chebyshev functions are asymptotic to x, a statement equivalent to the prime number theorem
.
Both functions are named in honour of Pafnuty Chebyshev
.
where k is the unique integer such that pk ≤ x but pk+1 > x. A more direct relationship is given by
Note that this last sum has only a finite number of non-vanishing terms, as
The second Chebyshev function is the logarithm of the least common multiple
of the integers from 1 to n.
for 
for k ≥ 198,
for x ≥ 10,544,111,
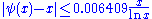for x ≥ exp(22),
for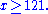 
Further, under the Riemann hypothesis
,
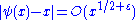
for any
proved an explicit expression for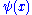
as a sum over the nontrivial zeros of the Riemann zeta function:
(The numerical value of ζ'(0)/ζ(0) is log(2π).) Here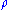
runs over the nontrivial zeros of the zeta function, and ψ0 is the same as ψ, except that at its jump discontinuities (the prime powers) it takes the value halfway between the values to the left and the right:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Chebyshev function is either of two related functions. The first Chebyshev function ϑ(x) or θ(x) is given by
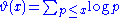
with the sum extending over all prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s p that are less than or equal to x.
The second Chebyshev function ψ(x) is defined similarly, with the sum extending over all prime powers not exceeding x:
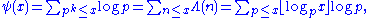
where
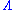is the von Mangoldt functionVon Mangoldt function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
. The Chebyshev function is often used in proofs related to prime numbers, because it is typically simpler to work with than the prime-counting function, π(x). Both Chebyshev functions are asymptotic to x, a statement equivalent to the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
.
Both functions are named in honour of Pafnuty Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
.
Relationships
The second Chebyshev function can be seen to be related to the first by writing it aswhere k is the unique integer such that pk ≤ x but pk+1 > x. A more direct relationship is given by
Note that this last sum has only a finite number of non-vanishing terms, as
The second Chebyshev function is the logarithm of the least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
of the integers from 1 to n.
Asymptotics and bounds
The following bounds are known for the Chebyshev functions: (in these formulas pk is the kth prime number p1 = 2, p2 = 3, etc.) for for k ≥ 198, for x ≥ 10,544,111,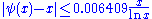 for x ≥ exp(22), for 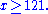Further, under the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
,
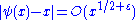
for any
The exact formula
In 1895, Hans Carl Friedrich von MangoldtHans Carl Friedrich von Mangoldt
Hans Carl Friedrich von Mangoldt was a German mathematician who contributed to the solution of the prime number theorem.Von Mangoldt completed his Doctor of Philosophy in 1878 at the University of Berlin, where his advisors were Ernst Kummer and Karl Weierstrass...
proved an explicit expression for
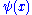as a sum over the nontrivial zeros of the Riemann zeta function:
(The numerical value of ζ'(0)/ζ(0) is log(2π).) Here
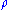runs over the nontrivial zeros of the zeta function, and ψ0 is the same as ψ, except that at its jump discontinuities (the prime powers) it takes the value halfway between the values to the left and the right:-
From the Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for the logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, the last term in the explicit formula can be understood as a summation of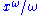
over the trivial zeros of the zeta function, 
, i.e.
Similarly, the first term, x = x1/1, corresponds to the simple pole of the zeta function at 1. Its being a pole rather than zero accounts for the opposite sign of the term.
Properties
A theorem due to Erhard SchmidtErhard SchmidtErhard Schmidt was a German mathematician whose work significantly influenced the direction of mathematics in the twentieth century. He was born in Tartu, Governorate of Livonia . His advisor was David Hilbert and he was awarded his doctorate from Georg-August University of Göttingen in 1905...
states that, for some explicit positive constant K, there are infinitely many natural numbers x such that
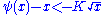
and infinitely many natural numbers x such that
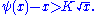
In little-o notation, one may write the above as
HardyG. H. HardyGodfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Littlewood prove the stronger result, that
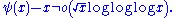
Relation to primorials
The first Chebyshev function is the logarithm of the primorialPrimorialIn mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
of x, denoted x#:
This proves that the primorial x# is asymptotically equal to exp((1+o(1))x), where "o" is the little-o notation (see Big O notationBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
) and together with the prime number theorem establishes the asymptotic behavior of pn#.
Relation to the prime-counting function
The Chebyshev function can be related to the prime-counting function as follows. Define
Then
The transition from
to the prime-counting function, 
, is made through the equation
Certainly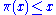
, so for the sake of approximation, this last relation can be recast in the form
The Riemann hypothesis
The Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
states that all nontrivial zeros of the zeta function have real part 1/2. In this case,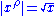
, and it can be shown that
By the above, this implies
Good evidence that RH could be true comes from the fact proposed by Alain ConnesAlain ConnesAlain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and others, that if we differentiate the von Mangoldt formula with respect to x make x = exp(u). Manipulating, we have the "Trace formula" for the exponential of the Hamiltonian operator satisfying
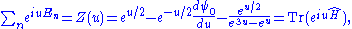
where the "trigonometric sum" can be considered to be the trace of the operator (statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
)
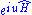,which is only true if 
Using the semiclassical approach the potential of H = T + V satisfies:
with Z(u) → 0 as u → ∞.
solution to this nonlinear integral equation can be obtained (among others) by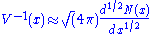
in order to obtain the inverse of the potential :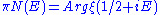 
Smoothing function
The smoothing function is defined as
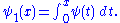
It can be shown that
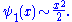
Variational formulation
The Chebyshev function evaluated at x = exp(t) minimizes the functional
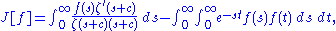
so
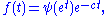
for c > 0.
External links
- Riemann's Explicit Formula, with images and movies
-
