Least common multiple
Encyclopedia
In arithmetic
and number theory
, the least common multiple (also called the lowest common multiple or smallest common multiple) of two integer
s a and b, usually denoted by LCM(a, b), is the smallest positive integer that is a multiple
of both a and b. It is familiar from grade-school arithmetic as the "lowest common denominator" that must be determined before two fractions
can be added.
If either a or b is 0, LCM(a, b) is defined to be zero.
The LCM of more than two integers is also well-defined: it is the smallest number that is an integer multiple of each of them.
Multiples of 4 are:
and the multiples of 6 are:
Common multiples of 4 and 6 are simply the numbers that are in both lists:
So the least common multiple of 4 and 6 is the smallest one of those: 12
, because each of the fractions can be expressed as a fraction with this denominator. For instance,

where the denominator 42 was used because it is the least common multiple of 21 and 6.
(GCD):

This formula is also valid when exactly one of a and b is 0, since gcd(a, 0) = |a|.
There are fast algorithm
s for computing the GCD that do not require the numbers to be factored, such as the Euclidean algorithm
. To return to the example above,

Because gcd(a, b) is a divisor of both a and b, it's more efficient to compute the LCM by dividing before multiplying:

This reduces the size of one input for both the division and the multiplication, and reduces the required storage needed for intermediate results (overflow in the a×b computation). Because gcd(a, b) is a divisor of both a and b, and thus the division will be guaranteed to yield an integer, so the intermediate result can be stored in an integer. Done this way, the previous example becomes:

says that every positive integer greater than 1 can be written in only one way as a product of prime number
s. The prime numbers can be considered as the atomic elements which, when combined together, make up a composite number
.
For example:

Here we have the composite number 90 made up of one atom of the prime number 2, two atoms of the prime number 3 and one atom of the prime number 5.
This knowledge can be used to find the lcm of a set of numbers.
Example: Find the value of lcm(8,9,21).
First, factor out each number and express it as a product of prime number powers.


The lcm will be the product of multiplying the highest power in each prime factor category together. Out of the 4 prime factor categories 2, 3, 5, and 7, the highest powers from each are 23, 32, 50, and 71. Thus,

This method is not as efficient as reducing to the greatest common divisor, since there is no known general efficient algorithm for integer factorization
, but is useful in illustrating concepts.
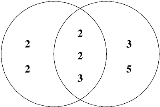
This method can be illustrated using a Venn diagram
as follows. Find the prime factorization of each of the two numbers. Put the prime factors into a Venn diagram with one circle for each of the two numbers, and all factors they share in common in the intersection. To find the LCM, just multiply all of the prime numbers in the diagram.
Here is an example:
and what they share in common is two "2"s and a "3":
This also works for the greatest common divisor
(GCD), except that instead of multiplying all of the numbers in the Venn diagram, one multiplies only the prime factors that are in the intersection. Thus the GCD of 48 and 180 is 2 × 2 × 3 = 12.
Let there be a finite sequence of positive integers X = (x1, x2, ..., xn), n > 1. The algorithm proceeds in steps as follows: on each step m it examines and updates the sequence X(m) = (x1(m), x2(m), ..., xn(m)), X(1) = X. The purpose of the examination is to pick up the least (perhaps, one of many) element of the sequence X(m). Assuming xk0(m) is the selected element, the sequence X(m+1) is defined as
In other words, the least element is increased by the corresponding x whereas the rest of the elements pass from X(m) to X(m+1) unchanged.
The algorithm stops when all elements in sequence X(m) are equal. Their common value L is exactly LCM(X). (For a proof and an interactive simulation see reference below, Algorithm for Computing the LCM.)
The process begins by dividing all of the factors by 2. If any of them divides evenly, write 2 at the top of the table and the result of division by 2 of each factor in the space to the right of each factor and below the 2. If they do not divide evenly, just rewrite the number again. If 2 does not divide evenly into any of the numbers, try 3.
Now, check if 2 divides again:
Once 2 no longer divides, divide by 3. If 3 no longer divides, try 5 and 7. Keep going until all of the numbers have been reduced to 1.
Now, multiply the numbers on the top and you have the LCM. In this case, it is 2 × 2 × 3 × 7 = 84. This is a variation on Euclid's algorithm, as common factors are essentially divided out along the way of dividing all of the numbers at once by each successive factor. You will get to the LCM the quickest if you use prime numbers and start from the lowest prime, 2.
a positive integer is the product of prime number
s, and, except for their order, this representation is unique:

where the exponents n2, n3, ... are non-negative integers; for example, 84 = 22 31 50 71 110 130 ...
Given two integers and
and  their least common multiple and greatest common divisor are given by the formulas
their least common multiple and greatest common divisor are given by the formulas

and
Since
this gives
In fact, any rational number can be written uniquely as the product of primes if negative exponents are allowed. When this is done, the above formulas remain valid. Using the same examples as above:


Under this ordering, the positive integers become a lattice
with meet
given by the gcd and join given by the lcm. The proof is straightforward, if a bit tedious; it amounts to checking that lcm and gcd satisfy the axioms for meet and join. Putting the lcm and gcd into this more general context establishes a duality
between them:
The following pairs of dual formulas are special cases of general lattice-theoretic identities.
It can also be shown that this lattice is distributive
, i.e. that lcm distributes over gcd and, dually, that gcd distributes over lcm:


This identitity is self-dual:
Then

where the absolute bars || denote the cardinality of a set.
s as follows: Let a and b be elements of a commutative ring R. A common multiple of a and b is an element m of R such that both a and b divide m (i.e. there exist elements x and y of R such that ax = m and by = m). A least common multiple of a and b is a common multiple that is minimal in the sense that for any other common multiple n of a and b, m divides n.
In general, two elements in a commutative ring can have no least common multiple or more than one. However, any two least common multiples of the same pair of elements are associates
. In a unique factorization domain
, any two elements have a least common multiple. In a principal ideal domain
, the least common multiple of a and b can be characterised as a generator of the intersection of the ideals generated by a and b (the intersection of a collection of ideals is always an ideal). In principal ideal domains, one can even talk about the least common multiple of arbitrary collections of elements: it is a generator of the intersection of the ideals generated by the elements of the collection.
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the least common multiple (also called the lowest common multiple or smallest common multiple) of two integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s a and b, usually denoted by LCM(a, b), is the smallest positive integer that is a multiple
Multiple (mathematics)
In mathematics, a multiple is the product of any quantity and an integer. In other words, for the quantities a and b, we say that b is a multiple of a if b = na for some integer n , which is called the multiplier or coefficient. If a is not zero, this is equivalent to saying that b/a is an integer...
of both a and b. It is familiar from grade-school arithmetic as the "lowest common denominator" that must be determined before two fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
can be added.
If either a or b is 0, LCM(a, b) is defined to be zero.
The LCM of more than two integers is also well-defined: it is the smallest number that is an integer multiple of each of them.
Example
What is the LCM of 4 and 6?Multiples of 4 are:
- 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76 etc.
and the multiples of 6 are:
- 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...
Common multiples of 4 and 6 are simply the numbers that are in both lists:
- 12, 24, 36, 48, 60, 72, ....
So the least common multiple of 4 and 6 is the smallest one of those: 12
Applications
When adding, subtracting, or comparing vulgar fractions, it is useful to find the least common multiple of the denominators, often called the lowest common denominatorLowest common denominator
In mathematics, the lowest common denominator or least common denominator is the least common multiple of the denominators of a set of vulgar fractions...
, because each of the fractions can be expressed as a fraction with this denominator. For instance,

where the denominator 42 was used because it is the least common multiple of 21 and 6.
Reduction by the greatest common divisor
The following formula reduces the problem of computing the least common multiple to the problem of computing the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(GCD):

This formula is also valid when exactly one of a and b is 0, since gcd(a, 0) = |a|.
There are fast algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s for computing the GCD that do not require the numbers to be factored, such as the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
. To return to the example above,

Because gcd(a, b) is a divisor of both a and b, it's more efficient to compute the LCM by dividing before multiplying:

This reduces the size of one input for both the division and the multiplication, and reduces the required storage needed for intermediate results (overflow in the a×b computation). Because gcd(a, b) is a divisor of both a and b, and thus the division will be guaranteed to yield an integer, so the intermediate result can be stored in an integer. Done this way, the previous example becomes:

Finding least common multiples by prime factorization
The unique factorization theoremFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
says that every positive integer greater than 1 can be written in only one way as a product of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. The prime numbers can be considered as the atomic elements which, when combined together, make up a composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
.
For example:

Here we have the composite number 90 made up of one atom of the prime number 2, two atoms of the prime number 3 and one atom of the prime number 5.
This knowledge can be used to find the lcm of a set of numbers.
Example: Find the value of lcm(8,9,21).
First, factor out each number and express it as a product of prime number powers.



The lcm will be the product of multiplying the highest power in each prime factor category together. Out of the 4 prime factor categories 2, 3, 5, and 7, the highest powers from each are 23, 32, 50, and 71. Thus,

This method is not as efficient as reducing to the greatest common divisor, since there is no known general efficient algorithm for integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
, but is useful in illustrating concepts.
This method can be illustrated using a Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
as follows. Find the prime factorization of each of the two numbers. Put the prime factors into a Venn diagram with one circle for each of the two numbers, and all factors they share in common in the intersection. To find the LCM, just multiply all of the prime numbers in the diagram.
Here is an example:
- 48 = 2 × 2 × 2 × 2 × 3,
- 180 = 2 × 2 × 3 × 3 × 5,
and what they share in common is two "2"s and a "3":
- Least common multiple = 2 × 2 × 2 × 2 × 3 × 3 × 5 = 720
- Greatest common divisor = 2 × 2 × 3 = 12
This also works for the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(GCD), except that instead of multiplying all of the numbers in the Venn diagram, one multiplies only the prime factors that are in the intersection. Thus the GCD of 48 and 180 is 2 × 2 × 3 = 12.
A simple algorithm
This method works as easily for finding the LCM of several integers.Let there be a finite sequence of positive integers X = (x1, x2, ..., xn), n > 1. The algorithm proceeds in steps as follows: on each step m it examines and updates the sequence X(m) = (x1(m), x2(m), ..., xn(m)), X(1) = X. The purpose of the examination is to pick up the least (perhaps, one of many) element of the sequence X(m). Assuming xk0(m) is the selected element, the sequence X(m+1) is defined as
- xk(m+1) = xk(m), k ≠ k0
- xk0(m+1) = xk0(m) + xk0.
In other words, the least element is increased by the corresponding x whereas the rest of the elements pass from X(m) to X(m+1) unchanged.
The algorithm stops when all elements in sequence X(m) are equal. Their common value L is exactly LCM(X). (For a proof and an interactive simulation see reference below, Algorithm for Computing the LCM.)
A method using a table
This method works for any number of factors. One begins by listing all of the numbers vertically in a table (in this example 4, 7, 12, 21, and 42):- 4
- 7
- 12
- 21
- 42
The process begins by dividing all of the factors by 2. If any of them divides evenly, write 2 at the top of the table and the result of division by 2 of each factor in the space to the right of each factor and below the 2. If they do not divide evenly, just rewrite the number again. If 2 does not divide evenly into any of the numbers, try 3.
| x | 2 |
|---|---|
| 4 | 2 |
| 7 | 7 |
| 12 | 6 |
| 21 | 21 |
| 42 | 21 |
Now, check if 2 divides again:
| x | 2 | 2 |
|---|---|---|
| 4 | 2 | 1 |
| 7 | 7 | 7 |
| 12 | 6 | 3 |
| 21 | 21 | 21 |
| 42 | 21 | 21 |
Once 2 no longer divides, divide by 3. If 3 no longer divides, try 5 and 7. Keep going until all of the numbers have been reduced to 1.
| x | 2 | 2 | 3 | 7 |
|---|---|---|---|---|
| 4 | 2 | 1 | 1 | 1 |
| 7 | 7 | 7 | 7 | 1 |
| 12 | 6 | 3 | 1 | 1 |
| 21 | 21 | 21 | 7 | 1 |
| 42 | 21 | 21 | 7 | 1 |
Now, multiply the numbers on the top and you have the LCM. In this case, it is 2 × 2 × 3 × 7 = 84. This is a variation on Euclid's algorithm, as common factors are essentially divided out along the way of dividing all of the numbers at once by each successive factor. You will get to the LCM the quickest if you use prime numbers and start from the lowest prime, 2.
Fundamental theorem of arithmetic
According to the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
a positive integer is the product of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, and, except for their order, this representation is unique:

where the exponents n2, n3, ... are non-negative integers; for example, 84 = 22 31 50 71 110 130 ...
Given two integers
 and
and  their least common multiple and greatest common divisor are given by the formulas
their least common multiple and greatest common divisor are given by the formulas
and

Since

this gives

In fact, any rational number can be written uniquely as the product of primes if negative exponents are allowed. When this is done, the above formulas remain valid. Using the same examples as above:



Lattice-theoretic
The positive integers may be partially ordered by divisibility: if a divides b (i.e. if b is an integer multiple of a) write a ≤ b (or equivalently, b ≥ a). (Forget the usual magnitude-based definition of ≤ in this section - it isn't used.)Under this ordering, the positive integers become a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
with meet
Meet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
given by the gcd and join given by the lcm. The proof is straightforward, if a bit tedious; it amounts to checking that lcm and gcd satisfy the axioms for meet and join. Putting the lcm and gcd into this more general context establishes a duality
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
between them:
- If a formula involving integer variables, gcd, lcm, ≤ and ≥ is true, then the formula obtained by switching gcd with lcm and switching ≥ with ≤ is also true. (Remember ≤ is defined as divides).
The following pairs of dual formulas are special cases of general lattice-theoretic identities.
Commutative laws   |
Associative laws Associativity In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...   |
Absorption law Absorption law In algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.Two binary operations, say ¤ and *, are said to be connected by the absorption law if:... s:   |
Idempotent laws   . . |
Define divides in terms of lcm and gcd   |
It can also be shown that this lattice is distributive
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
, i.e. that lcm distributes over gcd and, dually, that gcd distributes over lcm:


This identitity is self-dual:

Other
Let D be the product of ω(D) distinct prime numbers (i.e. D is squarefree).Then

where the absolute bars || denote the cardinality of a set.
The LCM in commutative rings
The least common multiple can be defined generally over commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s as follows: Let a and b be elements of a commutative ring R. A common multiple of a and b is an element m of R such that both a and b divide m (i.e. there exist elements x and y of R such that ax = m and by = m). A least common multiple of a and b is a common multiple that is minimal in the sense that for any other common multiple n of a and b, m divides n.
In general, two elements in a commutative ring can have no least common multiple or more than one. However, any two least common multiples of the same pair of elements are associates
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
. In a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
, any two elements have a least common multiple. In a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
, the least common multiple of a and b can be characterised as a generator of the intersection of the ideals generated by a and b (the intersection of a collection of ideals is always an ideal). In principal ideal domains, one can even talk about the least common multiple of arbitrary collections of elements: it is a generator of the intersection of the ideals generated by the elements of the collection.

