Sieve of Eratosthenes
Encyclopedia
In mathematics
, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm
for finding all prime number
s up to a specified integer.
It is one of the most efficient ways to find all of the smaller primes (below 10 million or so).
The algorithm is named after Eratosthenes of Cyrene
, an ancient Greek mathematician; although none of his works have survived, the sieve was described and attributed to Eratosthenes in the Introduction to Arithmetic
by Nicomachus
.
is a natural number
which has exactly two distinct natural number divisor
s: 1 and itself.
To find all the prime numbers less than or equal to a given integer n by Eratosthenes' method:
When the algorithm terminates, all the numbers in the list that are not marked are prime.
As a refinement, it is sufficient to mark the numbers in step 3 starting from p2, as all the smaller multiples of p will have already been marked at that point. This means that the algorithm is allowed to terminate in step 5 when p2 is greater than n. This does not appear in the original algorithm.
Another refinement is to initially list odd numbers only (3, 5, ..., n), and count up using an increment of 2p in step 3, thus marking only odd multiples of p greater than p itself. This refinement actually appears in the original description. This can be generalized with wheel factorization
, forming the initial list only from numbers coprime
with the first few primes and not just from odds, i.e. numbers coprime with 2.
can be used to produce primes by filtering out the composites found by testing each candidate number for divisibility by its preceding primes. It is often confused with the sieve of Eratosthenes, although the latter directly generates the composites instead of testing for them. Trial division has worse theoretical complexity
than that of the sieve of Eratosthenes in generating ranges of primes.
When testing each candidate number, the optimal trial division algorithm uses just those prime numbers not exceeding its square root. The widely known 1975 functional
code by David Turner
is often presented as an example of the sieve of Eratosthenes but is actually a sub-optimal trial division algorithm.
First generate a list of integers from 2 to 30:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
First number in the list is 2; cross out every 2nd number in the list after it (by counting up in increments of 2), i.e. all the multiples of 2:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Next number in the list after 2 is 3; cross out every 3-rd number in the list after it (by counting up in increments of 3), i.e. all the multiples of 3:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Next number not yet crossed out in the list after 3 is 5; cross out every 5-th number in the list after it (by counting up in increments of 5), i.e. all the multiples of 5:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Next number not yet crossed out in the list after 5 is 7; the next step would be to cross out every 7-th number in the list after it, but they are all already crossed out at this point, as these numbers (14, 21, 28) are also multiples of smaller primes because 7*7 is greater than 30. The numbers left not crossed out in the list at this point are all the prime numbers below 30:
2 3 5 7 11 13 17 19 23 29
model is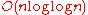
operations, a direct consequence of the fact that the prime harmonic series asymptotically approaches 
.
The bit complexity of the algorithm is
bit operations with a memory requirement of 
.
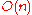The segmented version of the sieve of Eratosthenes, with basic optimizations, uses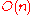
operations and 
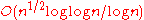bits of memory.
Input: an integer n > 1
Let A be an array of Boolean values, indexed by integers 2 to n,
initially all set to true.
for i = 2, 3, 4, ..., while i ≤ n/2:
if A[i] is true:
for j = 2i, 3i, 4i, ..., while j ≤ n:
A[j] = false
Now all i such that A[i] is true are prime.
Large ranges may not fit entirely in memory. In these cases it is necessary to use a segmented sieve where only portions of the range are sieved at a time. For ranges so large that the sieving primes could not be held in memory, space-efficient sieves like that of Sorenson are used instead.
[2] (3) 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 ...
[3] (5) 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 ...
[4] (7) 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 ...
[5] (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ...
[...]
Here the example is shown starting from odds, after the 1st step of the algorithm. Thus on k-th step all the multiples of the k-th prime are removed from the list. If generating a bounded sequence of primes, when the next identified prime exceeds the square root of the upper limit, all the remaining numbers in the list are prime. In the example given above that is achieved on identifying 11 as next prime, giving a list of all primes less than or equal to 80.
Note that numbers that will be discarded by some step are still used while marking the multiples, e.g. for the multiples of 3 it is , , , , ..., , ... .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for finding all prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s up to a specified integer.
It is one of the most efficient ways to find all of the smaller primes (below 10 million or so).
The algorithm is named after Eratosthenes of Cyrene
Eratosthenes
Eratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...
, an ancient Greek mathematician; although none of his works have survived, the sieve was described and attributed to Eratosthenes in the Introduction to Arithmetic
Introduction to Arithmetic
Introduction to Arithmetic was written by Nicomachus almost two thousand years ago, and contains both philosophical prose and very basic mathematical ideas. Nicomachus refers to Plato quite often, and wrote about how philosophy can only be possible if one knows enough about mathematics. This is...
by Nicomachus
Nicomachus
Nicomachus was an important mathematician in the ancient world and is best known for his works Introduction to Arithmetic and Manual of Harmonics in Greek. He was born in Gerasa, in the Roman province of Syria , and was strongly influenced by Aristotle...
.
Algorithm description
A prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
which has exactly two distinct natural number divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s: 1 and itself.
To find all the prime numbers less than or equal to a given integer n by Eratosthenes' method:
- Create a list of consecutive integers from 2 to n: (2, 3, 4, ..., n).
- Initially, let p equal 2, the first prime number.
- Starting from p, count up in increments of p and mark each of these numbers greater than p itself in the list. These numbers will be 2p, 3p, 4p, etc.; note that some of them may have already been marked.
- Find the first number greater than p in the list that is not marked; let p now equal this number (which is the next prime).
- If there were no more unmarked numbers in the list, stop. Otherwise, repeat from step 3.
When the algorithm terminates, all the numbers in the list that are not marked are prime.
As a refinement, it is sufficient to mark the numbers in step 3 starting from p2, as all the smaller multiples of p will have already been marked at that point. This means that the algorithm is allowed to terminate in step 5 when p2 is greater than n. This does not appear in the original algorithm.
Another refinement is to initially list odd numbers only (3, 5, ..., n), and count up using an increment of 2p in step 3, thus marking only odd multiples of p greater than p itself. This refinement actually appears in the original description. This can be generalized with wheel factorization
Wheel factorization
Wheel factorization is a graphical method for manually performing a preliminary to the Sieve of Eratosthenes that separates prime numbers from composites. Start by writing the natural numbers around circles as shown below. Prime numbers in the innermost circle have their multiples in similar...
, forming the initial list only from numbers coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
with the first few primes and not just from odds, i.e. numbers coprime with 2.
Incremental sieve
An incremental formulation of the sieve generates primes indefinitely (i.e. without an upper bound) by interleaving the generation of primes with the generation of their multiples (so that primes can be found in gaps between the multiples), where the multiples of each prime p are generated directly, by counting up from the square of the prime in increments of p (or 2p for odd primes).Trial division
Trial divisionTrial division
Trial division is the most laborious but easiest to understand of the integer factorization algorithms. Its ease of implementation makes it a viable integer factorization option for devices with little available memory, such as graphing calculators....
can be used to produce primes by filtering out the composites found by testing each candidate number for divisibility by its preceding primes. It is often confused with the sieve of Eratosthenes, although the latter directly generates the composites instead of testing for them. Trial division has worse theoretical complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
than that of the sieve of Eratosthenes in generating ranges of primes.
When testing each candidate number, the optimal trial division algorithm uses just those prime numbers not exceeding its square root. The widely known 1975 functional
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
code by David Turner
David Turner (computer scientist)
Professor David Turner is a British computer scientist.He has a D.Phil. from the University of Oxford. He has held professorships at Queen Mary College, London, University of Texas at Austin and the University of Kent at Canterbury, where he now retains the post of Emeritus Professor.He is...
is often presented as an example of the sieve of Eratosthenes but is actually a sub-optimal trial division algorithm.
Example
To find all the prime numbers less than or equal to 30, proceed as follows.First generate a list of integers from 2 to 30:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
First number in the list is 2; cross out every 2nd number in the list after it (by counting up in increments of 2), i.e. all the multiples of 2:
2 3
Next number in the list after 2 is 3; cross out every 3-rd number in the list after it (by counting up in increments of 3), i.e. all the multiples of 3:
2 3
Next number not yet crossed out in the list after 3 is 5; cross out every 5-th number in the list after it (by counting up in increments of 5), i.e. all the multiples of 5:
2 3
Next number not yet crossed out in the list after 5 is 7; the next step would be to cross out every 7-th number in the list after it, but they are all already crossed out at this point, as these numbers (14, 21, 28) are also multiples of smaller primes because 7*7 is greater than 30. The numbers left not crossed out in the list at this point are all the prime numbers below 30:
2 3 5 7 11 13 17 19 23 29
Algorithm complexity
Time complexity in random access machineRandom access machine
In computer science, random access machine is an abstract machine in the general class of register machines. The RAM is very similar to the counter machine but with the added capability of 'indirect addressing' of its registers...
model is
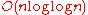operations, a direct consequence of the fact that the prime harmonic series asymptotically approaches .The bit complexity of the algorithm is
bit operations with a memory requirement of 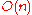.The segmented version of the sieve of Eratosthenes, with basic optimizations, uses
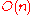operations and 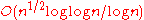bits of memory.Implementation
In pseudocode:Input: an integer n > 1
Let A be an array of Boolean values, indexed by integers 2 to n,
initially all set to true.
for i = 2, 3, 4, ..., while i ≤ n/2:
if A[i] is true:
for j = 2i, 3i, 4i, ..., while j ≤ n:
A[j] = false
Now all i such that A[i] is true are prime.
Large ranges may not fit entirely in memory. In these cases it is necessary to use a segmented sieve where only portions of the range are sieved at a time. For ranges so large that the sieving primes could not be held in memory, space-efficient sieves like that of Sorenson are used instead.
Euler's sieve
Euler's proof of the zeta product formula contains version of the sieve of Eratosthenes in which each composite number is eliminated exactly once. It, too, starts with a list of numbers from 2 to n in order. On each step the first element is identified as the next prime and the results of multiplying this prime with each element of the list are marked in the list for subsequent deletion. The initial element and the marked elements are then removed from the working sequence, and the process is repeated:[2] (3) 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 ...
[3] (5) 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 ...
[4] (7) 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 ...
[5] (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ...
[...]
Here the example is shown starting from odds, after the 1st step of the algorithm. Thus on k-th step all the multiples of the k-th prime are removed from the list. If generating a bounded sequence of primes, when the next identified prime exceeds the square root of the upper limit, all the remaining numbers in the list are prime. In the example given above that is achieved on identifying 11 as next prime, giving a list of all primes less than or equal to 80.
Note that numbers that will be discarded by some step are still used while marking the multiples, e.g. for the multiples of 3 it is , , , , ..., , ... .
External links
- Interactive JavaScript Page
- Sieve of Eratosthenes by George Beck, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Sieve of Eratosthenes in Haskell
- Sieve of Eratosthenes algorithm illustrated and explained. Java and C++ implementations.
- A simplified C++ version of a sieve based upon the Sieve of Eratosthenes (some minor optimization)
- A highly optimized Sieve of Eratosthenes in C
- A parallel implementation in C#
- SieveOfEratosthenesInManyProgrammingLanguages c2 wiki page