
Jacobi symbol
Encyclopedia
The Jacobi symbol is a generalization of the Legendre symbol
. Introduced by Jacobi
in 1837, it is of theoretical interest in modular arithmetic
and other branches of number theory
, but its main use is in computational number theory
, especially primality testing and integer factorization
; these in turn are important in cryptography
.
s corresponding to the prime factors of n:
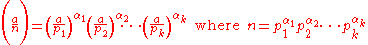
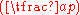 represents the Legendre symbol, defined for all integers a and all odd primes p by
represents the Legendre symbol, defined for all integers a and all odd primes p by
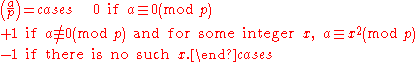
Following the normal convention for the empty product,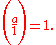
Keep in mind that Jacobi symbols are only defined when the upper argument ("numerator") is an integer and the lower argument ("denominator") is a positive odd integer.
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
. Introduced by Jacobi
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
in 1837, it is of theoretical interest in modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
and other branches of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, but its main use is in computational number theory
Computational number theory
In mathematics, computational number theory, also known as algorithmic number theory, is the study of algorithms for performing number theoretic computations...
, especially primality testing and integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
; these in turn are important in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
.
Definition
For any integer a and any positive odd integer n the Jacobi symbol is defined as the product of the Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
s corresponding to the prime factors of n:
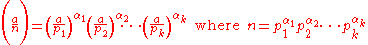
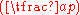 represents the Legendre symbol, defined for all integers a and all odd primes p by
represents the Legendre symbol, defined for all integers a and all odd primes p by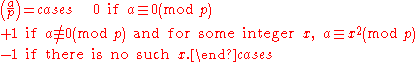
Following the normal convention for the empty product,
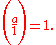
Properties
These facts, even the reciprocity laws, are straightforward deductions from the definition of the Jacobi symbol and the corresponding properties of the Legendre symbol.Keep in mind that Jacobi symbols are only defined when the upper argument ("numerator") is an integer and the lower argument ("denominator") is a positive odd integer.
- 1) If
 is (an odd) prime, then the Jacobi symbol
is (an odd) prime, then the Jacobi symbol  is also a Legendre symbol.
is also a Legendre symbol.
- 2) If
 then
then 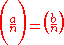
- 3)
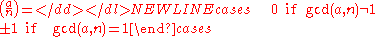
- 4)
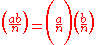 , so
, so 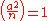 (or
(or  )
)
- 5)
 , so
, so 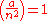 (or
(or  )
)
The law of quadratic reciprocity: if m and n are odd positive coprime integers, then
- 6)

and its supplements
- 7)
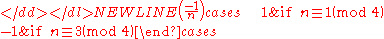
- 8)
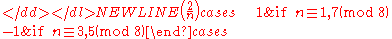
Like the Legendre symbol,
- If
 then
then  is a quadratic nonresidue
is a quadratic nonresidue 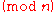
- If
 is a quadratic residue
is a quadratic residue 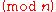 then
then 
But, unlike the Legendre symbol
- If
 then
then  may or may not be a quadratic residue
may or may not be a quadratic residue 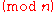 .
.
This is because for a to be a residue (mod n) it has to be a residue modulo every prime that divides n, but the Jacobi symbol will equal one if for example a is a non-residue for exactly two of the primes which divide n.
Although the Jacobi symbol can't be uniformly interpreted in terms of squares and non-squares, it can be uniformly interpreted as the sign of a permutation by Zolotarev's lemmaZolotarev's lemmaIn number theory, Zolotarev's lemma states that the Legendre symbol\leftfor an integer a modulo an odd prime number p, where p does not divide a, can be computed as the sign of a permutation:...
.
Calculating the Jacobi symbol
The above formulas lead to an efficient algorithm for calculating the Jacobi symbol, analogous to the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
for finding the GCD of two numbers. (This should not be surprising in light of rule 3)).
The "numerator" is reduced modulo the "denominator" using rule 2). Any multiples of 2 are pulled out using rule 4) and calculated using rule 8). The symbol is flipped using rule 6), and the algorithm recurses until the "numerator" is 1 (covered by rule 4)) or 2 (covered by rule 8)), or the "numerator" equals the "denominator" (rule 3)).
Example of calculations
The Legendre symbol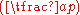 is only defined for odd primes p. It obeys the same rules as the Jacobi symbol (i.e., reciprocity and the supplementary formulas for
is only defined for odd primes p. It obeys the same rules as the Jacobi symbol (i.e., reciprocity and the supplementary formulas for 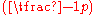 and
and  and multiplicativity of the "numerator".)
and multiplicativity of the "numerator".)

\left(\frac{7}{9907}\right) \left(\frac{11}{9907}\right) \left(\frac{13}{9907}\right).
-
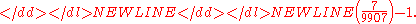
The difference between the two calculations is that when the Legendre symbol is used the "numerator" has to be factored into prime powers before the symbol is flipped. This makes the calculation using the Legendre symbol significantly slower than the one using the Jacobi symbol, as there is no known polynomial-time algorithm for factoring integers. In fact, this is why Jacobi introduced the symbol.
Primality testing
There is another way the Jacobi and Legendre symbols differ. If the Euler criterion formula is used modulo a composite number, the result may or may not be the value of the Jacobi symbol.
So if it's not known whether a number n is prime or composite, we can pick a random number a, calculate the Jacobi symbol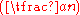 and compare it with Euler's formula; if they differ, n is composite; if they're the same for many different values of a, n is "probably prime".
and compare it with Euler's formula; if they differ, n is composite; if they're the same for many different values of a, n is "probably prime".
This is the basis for the probabilistic Solovay–Strassen primality test and its refinement the Miller–Rabin primality test.
External links
- Calculate Jacobi symbol shows the steps of the calculation.
- If
- 8)
- 7)
- 4)

