Carmichael number
Encyclopedia
In number theory
, a Carmichael number is a composite
positive integer
which satisfies the congruence
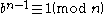
for all integers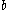
which are relatively prime to 
(see modular arithmetic
). They are named for Robert Carmichael
. The Carmichael numbers are the Knödel number
s K1.
states that all prime numbers have the above property. In this sense, Carmichael numbers are similar to prime numbers; in fact, they are called Fermat pseudoprimes. Carmichael numbers are sometimes also called absolute Fermat pseudoprimes.
Carmichael numbers are important because they pass the Fermat primality test
but are not actually prime. Since Carmichael numbers exist, this primality test cannot be relied upon to prove the primality of a number, although it can still be used to prove a number is composite.
Still, as numbers become larger, Carmichael numbers become very rare. For example, there are 20,138,200 Carmichael numbers between 1 and 1021 (approximately one in 50 billion numbers). This makes tests based on Fermat's Little Theorem slightly risky compared to others such as the Solovay-Strassen primality test
.
It follows from this theorem that all Carmichael numbers are odd, since any even composite number that is square-free (and hence has only one prime factor of two) will have at least one odd prime factor, and thus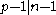
results in an even dividing an odd, a contradiction. (The oddness of Carmichael numbers also follows from the fact that 
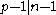is a Fermat witness
for any even number.)
From the criterion it also follows that Carmichael numbers are cyclic
.
That 561 is a Carmichael number can be seen with Korselt's criterion. Indeed,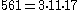
is square-free 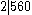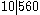and 
, 
and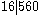 
.
The next few Carmichael numbers are :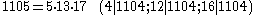
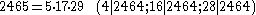
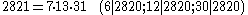
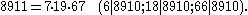
J. Chernick proved a theorem in 1939 which can be used to construct a subset
of Carmichael numbers. The number
is a Carmichael number if its three factors are all prime. Whether this formula produces an infinite quantity of Carmichael numbers is an open question (though it is implied by Dickson's conjecture
).
Paul Erdős
heuristically argued there should be infinitely many Carmichael numbers. In 1994 it was shown by W. R. (Red) Alford
, Andrew Granville
and Carl Pomerance
that there really do exist infinitely many Carmichael numbers. Specifically, they showed that for sufficiently large
, there are at least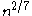 
Carmichael numbers between 1 and 
.
Löh and Niebuhr in 1992 found some huge Carmichael numbers, including one with 1,101,518 factors and over 16 million digits.
prime factors are :
The first Carmichael numbers with 4 prime factors are :
The second Carmichael number (1105) can be expressed as the sum of two squares in more ways than any smaller number. The third Carmichael number (1729
) is the Hardy-Ramanujan Number: the smallest number that can be expressed as the sum of two cubes in two different ways.
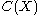denote the number of Carmichael numbers less than or equal to 
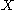. The distribution of Carmichael numbers by powers of 10:
In 1956, Erdős proved that
for some constant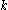
. He further gave a heuristic argument
suggesting that this upper bound should be close to the true growth rate of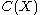
. The table below gives approximate minimal values for the constant k in the Erdős bound for 
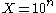as n grows:
In the other direction, Alford
, Granville
and Pomerance
proved in 1994 that for sufficiently large X,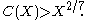
In 2005, this bound was further improved by Harman
to
and then has subsequently improved the exponent to just over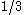
.
Regarding the asymptotic distribution of Carmichael numbers, there have been several conjectures. In 1956, Erdős conjectured that there were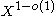
Carmichael numbers for X sufficiently large. In 1981, Pomerance sharpened Erdős' heuristic arguments to conjecture that there are
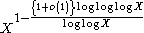
Carmichael numbers up to X. However, inside current computational ranges (such as the counts of Carmichael numbers performed by Pinch up to 1021), these conjectures are not yet borne out by the data. Utilizing finer estimates for the distribution of smooth numbers, Aran Nayebi has proposed a conjecture (defined as the function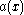
on pg. 31) that is asymptotically the same as Pomerance's, but more closely models the actual distribution of Carmichael numbers for the small bounds computed by Pinch and may provide accurate predictions for counts with bounds (< 10100) yet to be computed, particularly since its derivation involves a sharpening of Pomerance's (and Erdős') heuristic arguments.
.
The above definition states that a composite integer n is Carmichael
precisely when the nth-power-raising function pn from the ring
Zn of integers modulo n to itself is the identity function. The identity is the only Zn-algebra
endomorphism
on Zn so we can restate the definition as asking that pn be an algebra endomorphism of Zn.
As above, pn satisfies the same property whenever n is prime.
The nth-power-raising function pn is also defined on any Zn-algebra A. A theorem states that n is prime if and only if all such functions pn are algebra endomorphisms.
In-between these two conditions lies the definition of Carmichael number of order m for any positive integer m as any composite number n such that pn is an endomorphism on every Zn-algebra that can be generated as Zn-module
by m elements. Carmichael numbers of order 1 are just the ordinary Carmichael numbers.
A heuristic argument, given in the same paper, appears to suggest that there are infinitely many Carmichael numbers of order m, for any m. However, not a single Carmichael number of order 3 or above is known.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Carmichael number is a composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
which satisfies the congruenceModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
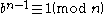
for all integers
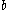which are relatively prime to (see modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
). They are named for Robert Carmichael
Robert Daniel Carmichael
Robert Daniel Carmichael was a leading American mathematician. Carmichael was born in Goodwater, Alabama. He attended Lineville College, briefly, and he earned his bachelor's degree in 1898, while he was studying towards his Ph.D. degree at Princeton University. Carmichael completed the...
. The Carmichael numbers are the Knödel number
Knödel number
A Knödel number for a given positive integer n is a composite number m with the property that each i A Knödel number for a given positive integer n is a composite number m with the property that each i...
s K1.
Overview
Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
states that all prime numbers have the above property. In this sense, Carmichael numbers are similar to prime numbers; in fact, they are called Fermat pseudoprimes. Carmichael numbers are sometimes also called absolute Fermat pseudoprimes.
Carmichael numbers are important because they pass the Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
but are not actually prime. Since Carmichael numbers exist, this primality test cannot be relied upon to prove the primality of a number, although it can still be used to prove a number is composite.
Still, as numbers become larger, Carmichael numbers become very rare. For example, there are 20,138,200 Carmichael numbers between 1 and 1021 (approximately one in 50 billion numbers). This makes tests based on Fermat's Little Theorem slightly risky compared to others such as the Solovay-Strassen primality test
Solovay-Strassen primality test
The Solovay–Strassen primality test, developed by Robert M. Solovay and Volker Strassen, is a probabilistic test to determine if a number is composite or probably prime...
.
Korselt's criterion
An alternative and equivalent definition of Carmichael numbers is given by Korselt's criterion.- Theorem (KorseltAlwin KorseltAlwin Reinhold Korselt was a German mathematician. He discovered Korselt's Criterion which provides a definition for Carmichael numbers and also contributed an early result in relational algebra.-Personal life:The Korselts are a huge, widespread family that has been resident in the village of...
1899): A positive composite integer
is a Carmichael number if and only if 
is square-freeSquare-free integerIn mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
, and for all prime divisors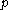
of 
, it is true that 
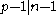(the notation 
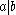indicates that 
dividesDivisorIn mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
).
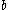It follows from this theorem that all Carmichael numbers are odd, since any even composite number that is square-free (and hence has only one prime factor of two) will have at least one odd prime factor, and thus
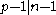results in an even dividing an odd, a contradiction. (The oddness of Carmichael numbers also follows from the fact that 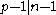is a Fermat witnessFermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
for any even number.)
From the criterion it also follows that Carmichael numbers are cyclic
Cyclic number (group theory)
A cyclic number is a natural number n such that n and φ are coprime. Here φ is Euler's totient function. An equivalent definition is that a number n is cyclic iff any group of order n is cyclic.Any prime number is clearly cyclic...
.
Discovery
Korselt was the first who observed the basic properties of Carmichael numbers, but he could not find any examples. In 1910, Carmichael found the first and smallest such number, 561, and hence the name "Carmichael number".That 561 is a Carmichael number can be seen with Korselt's criterion. Indeed,
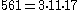is square-free 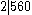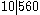and , and 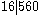.The next few Carmichael numbers are :
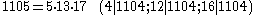
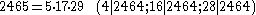
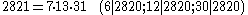
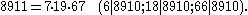
J. Chernick proved a theorem in 1939 which can be used to construct a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Carmichael numbers. The number
is a Carmichael number if its three factors are all prime. Whether this formula produces an infinite quantity of Carmichael numbers is an open question (though it is implied by Dickson's conjectureDickson's conjecture
In number theory, a branch of mathematics, Dickson's conjecture is the conjecture stated by that for a finite set of linear forms , , ..., with , there are infinitely many positive integers for which they are all prime, unless there is a congruence condition preventing this...
).
Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
heuristically argued there should be infinitely many Carmichael numbers. In 1994 it was shown by W. R. (Red) Alford
W. R. (Red) Alford
William Robert "Red" Alford was an American mathematician who worked in the field of number theory.-Biography:...
, Andrew Granville
Andrew Granville
Andrew James Granville is a British mathematician, working in the field of number theory.He has been a faculty member at the Université de Montréal since 2002. Before moving to Montreal he was a mathematics professor at University of Georgia from 1991 until 2002...
and Carl Pomerance
Carl Pomerance
Carl Bernard Pomerance is a well-known number theorist. He attended college at Brown University and later received his Ph.D. from Harvard University in 1972 with a dissertation proving that any odd perfect number has at least 7 distinct prime factors. He immediately joined the faculty at the...
that there really do exist infinitely many Carmichael numbers. Specifically, they showed that for sufficiently large
, there are at least 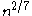Carmichael numbers between 1 and .Löh and Niebuhr in 1992 found some huge Carmichael numbers, including one with 1,101,518 factors and over 16 million digits.
Factorizations
Carmichael numbers have at least three positive prime factors. The first Carmichael numbers with prime factors are :| k | |
|---|---|
| 3 |  |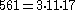
| 4 |  |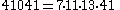
| 5 |  |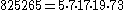
| 6 |  |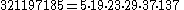
| 7 |  |
| 8 |  |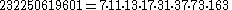
| 9 |  |
The first Carmichael numbers with 4 prime factors are :
| i | |
|---|---|
| 1 |  |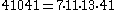
| 2 |  |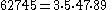
| 3 |  |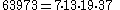
| 4 |  |
| 5 |  |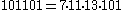
| 6 |  |
| 7 |  |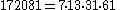
| 8 |  |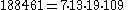
| 9 |  |
| 10 |  |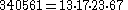
The second Carmichael number (1105) can be expressed as the sum of two squares in more ways than any smaller number. The third Carmichael number (1729
1729 (number)
1729 is the natural number following 1728 and preceding 1730.1729 is known as the Hardy–Ramanujan number after a famous anecdote of the British mathematician G. H. Hardy regarding a hospital visit to the Indian mathematician Srinivasa Ramanujan...
) is the Hardy-Ramanujan Number: the smallest number that can be expressed as the sum of two cubes in two different ways.
Distribution
Let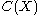 denote the number of Carmichael numbers less than or equal to 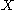. The distribution of Carmichael numbers by powers of 10:  |
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
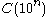1 | 7 | 16 | 43 | 105 | 255 | 646 | 1547 | 3605 | 8241 | 19279 | 44706 | 105212 | 246683 | 585355 | 1401644 | 3381806 | 8220777 | 20138200 |
In 1956, Erdős proved that
for some constant
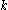. He further gave a heuristic argumentHeuristic argument
A heuristic argument is an argument that reasons from the value of a method or principle that has been shown by experimental investigation to be a useful aid in learning, discovery and problem-solving. A widely-used and important example of a heuristic argument is Occam's Razor....
suggesting that this upper bound should be close to the true growth rate of
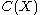. The table below gives approximate minimal values for the constant k in the Erdős bound for 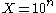as n grows:  |
4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|
| k | 2.19547 | 1.97946 | 1.90495 | 1.86870 | 1.86377 | 1.86293 | 1.86406 | 1.86522 | 1.86598 | 1.86619 |
In the other direction, Alford
W. R. (Red) Alford
William Robert "Red" Alford was an American mathematician who worked in the field of number theory.-Biography:...
, Granville
Andrew Granville
Andrew James Granville is a British mathematician, working in the field of number theory.He has been a faculty member at the Université de Montréal since 2002. Before moving to Montreal he was a mathematics professor at University of Georgia from 1991 until 2002...
and Pomerance
Carl Pomerance
Carl Bernard Pomerance is a well-known number theorist. He attended college at Brown University and later received his Ph.D. from Harvard University in 1972 with a dissertation proving that any odd perfect number has at least 7 distinct prime factors. He immediately joined the faculty at the...
proved in 1994 that for sufficiently large X,
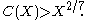
In 2005, this bound was further improved by Harman
Glyn Harman
Glyn Harman is a British mathematician working in analytic number theory. One of his major interests is prime number theory. He is best known for results on gaps between primes and the greatest prime factor of p + a, as well as his lower bound for the number of Carmichael numbers up to X...
to
and then has subsequently improved the exponent to just over
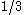.Regarding the asymptotic distribution of Carmichael numbers, there have been several conjectures. In 1956, Erdős conjectured that there were
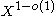Carmichael numbers for X sufficiently large. In 1981, Pomerance sharpened Erdős' heuristic arguments to conjecture that there are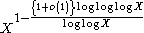Carmichael numbers up to X. However, inside current computational ranges (such as the counts of Carmichael numbers performed by Pinch up to 1021), these conjectures are not yet borne out by the data. Utilizing finer estimates for the distribution of smooth numbers, Aran Nayebi has proposed a conjecture (defined as the function
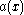on pg. 31) that is asymptotically the same as Pomerance's, but more closely models the actual distribution of Carmichael numbers for the small bounds computed by Pinch and may provide accurate predictions for counts with bounds (< 10100) yet to be computed, particularly since its derivation involves a sharpening of Pomerance's (and Erdős') heuristic arguments.Generalizations
Both prime and Carmichael numbers satisfy the following equalityHigher-order Carmichael numbers
Carmichael numbers can be generalized using concepts of abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
.
The above definition states that a composite integer n is Carmichael
precisely when the nth-power-raising function pn from the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
Zn of integers modulo n to itself is the identity function. The identity is the only Zn-algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
on Zn so we can restate the definition as asking that pn be an algebra endomorphism of Zn.
As above, pn satisfies the same property whenever n is prime.
The nth-power-raising function pn is also defined on any Zn-algebra A. A theorem states that n is prime if and only if all such functions pn are algebra endomorphisms.
In-between these two conditions lies the definition of Carmichael number of order m for any positive integer m as any composite number n such that pn is an endomorphism on every Zn-algebra that can be generated as Zn-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
by m elements. Carmichael numbers of order 1 are just the ordinary Carmichael numbers.
Properties
Korselt's criterion can be generalized to higher-order Carmichael numbers, as shown by Howe.A heuristic argument, given in the same paper, appears to suggest that there are infinitely many Carmichael numbers of order m, for any m. However, not a single Carmichael number of order 3 or above is known.