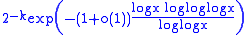Solovay-Strassen primality test
Encyclopedia
The Solovay–Strassen primality test
, developed by Robert M. Solovay
and Volker Strassen
, is a probabilistic
test to determine if a number is composite
or probably prime
. It has been largely superseded by the Miller–Rabin primality test, but has great historical importance in showing the practical feasibility of the RSA cryptosystem
.
proved that for an odd prime number
p and any integer a,
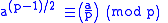
where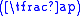
is the Legendre symbol
. The Jacobi symbol
is a generalisation of the Legendre symbol to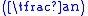
, where n can be any odd integer. The Jacobi symbol can be computed in time O
((log n)²) using Jacobi's generalization of
law of quadratic reciprocity
.
Given an odd number n we can contemplate whether or not the congruence
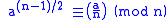
holds for various values of the "base" a. If n is prime then this congruence is true for all a. So if we pick values of a at random and test the congruence, then
as soon as we find an a which doesn't fit the congruence we know that n is not prime (but this does not tell us a nontrivial factorization of n). This base a is called an Euler witness for n; it is a witness for the compositeness of n. The base a is called an Euler liar for n if the congruence is true while n is composite.
For every composite odd n at least half of all bases
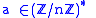
are (Euler) witnesses: this contrasts with the Fermat primality test
, for which the proportion of witnesses may be much smaller. Therefore, there are no (odd) composite n without lots of witnesses, unlike the case of Carmichael numbers for Fermat's test.
We randomly select an a = 47 < n. We compute:
This gives that, either 221 is prime, or 47 is an Euler liar for 221. We try another random a, this time choosing a = 2:
Hence 2 is an Euler witness for the compositeness of 221, and 47 was in fact an Euler liar. Note that this tells us nothing about the factors of 221 (which are 13 and 17).
as follows:
Inputs: n, a value to test for primality; k, a parameter that determines the accuracy of the test
Output: composite if n is composite, otherwise probably prime
repeat k times:
choose a randomly in the range [2,n − 1]
x ←
if x = 0 or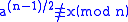
then return composite
return probably prime
Using fast algorithms for modular exponentiation
, the running time of this algorithm is O(k·log3 n), where k is the number of different values of a we test.
.
When n is odd and composite, at least half of all a with gcd(a,n) = 1 are Euler witnesses. We can prove this as follows: let {a1, a2, ..., am} be the Euler liars and a an Euler witness. Then, for i = 1,2,...,m:
Because the following holds: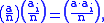
now we know that
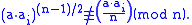
This gives that each ai gives a number a·ai, which is also an Euler witness.
So each Euler liar gives an Euler witness and so the number of Euler witnesses is larger or equal to the number of Euler liars. Therefore, when n is composite, at least half of all a with gcd(a,n) = 1 is an Euler witness.
Hence, the probability of failure is at most 2−k (compare this with the probability of failure for the Miller-Rabin primality test
, which is at most 4−k).
For purposes of cryptography
the more bases a we test, i.e. if we pick a sufficiently large value of k, the better the accuracy of test. Hence the chance of the algorithm failing in this way is so small that the (pseudo) prime is used in practice in cryptographic applications, but for applications for which it is important to have a prime, a test like ECPP
or Pocklington should be used which proves primality.
for k rounds of the test, applied to uniformly random . The same bound also applies to the related problem of what is the conditional probability of n being composite for a random number which has been declared prime in k rounds of the test.
COMPOSITE is in the complexity class
RP
.
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
, developed by Robert M. Solovay
Robert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
and Volker Strassen
Volker Strassen
Volker Strassen is a German mathematician, a professor emeritus in the department of mathematics and statistics at the University of Konstanz.-Biography:Strassen was born on April 29, 1936, in Düsseldorf-Gerresheim....
, is a probabilistic
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
test to determine if a number is composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
or probably prime
Probable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
. It has been largely superseded by the Miller–Rabin primality test, but has great historical importance in showing the practical feasibility of the RSA cryptosystem
Cryptosystem
There are two different meanings of the word cryptosystem. One is used by the cryptographic community, while the other is the meaning understood by the public.- General meaning :...
.
Concepts
EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
proved that for an odd prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p and any integer a,
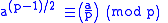
where
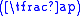is the Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
. The Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
is a generalisation of the Legendre symbol to
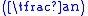, where n can be any odd integer. The Jacobi symbol can be computed in time OBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
((log n)²) using Jacobi's generalization of
law of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
.
Given an odd number n we can contemplate whether or not the congruence
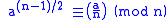
holds for various values of the "base" a. If n is prime then this congruence is true for all a. So if we pick values of a at random and test the congruence, then
as soon as we find an a which doesn't fit the congruence we know that n is not prime (but this does not tell us a nontrivial factorization of n). This base a is called an Euler witness for n; it is a witness for the compositeness of n. The base a is called an Euler liar for n if the congruence is true while n is composite.
For every composite odd n at least half of all bases
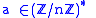
are (Euler) witnesses: this contrasts with the Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
, for which the proportion of witnesses may be much smaller. Therefore, there are no (odd) composite n without lots of witnesses, unlike the case of Carmichael numbers for Fermat's test.
Example
Suppose we wish to determine if n = 221 is prime. We write (n−1)/2=110.We randomly select an a = 47 < n. We compute:
- a(n−1)/2 mod n = 47110 mod 221 = −1 mod 221
-
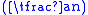mod n = 
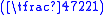mod 221 = −1 mod 221.
This gives that, either 221 is prime, or 47 is an Euler liar for 221. We try another random a, this time choosing a = 2:
- a(n−1)/2 mod n = 2110 mod 221 = 30 mod 221
-
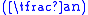mod n = 
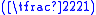mod 221 = −1 mod 221.
Hence 2 is an Euler witness for the compositeness of 221, and 47 was in fact an Euler liar. Note that this tells us nothing about the factors of 221 (which are 13 and 17).
Algorithm and running time
The algorithm can be written in pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
as follows:
Inputs: n, a value to test for primality; k, a parameter that determines the accuracy of the test
Output: composite if n is composite, otherwise probably prime
repeat k times:
choose a randomly in the range [2,n − 1]
x ←
if x = 0 or
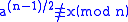then return compositereturn probably prime
Using fast algorithms for modular exponentiation
Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
, the running time of this algorithm is O(k·log3 n), where k is the number of different values of a we test.
Accuracy of the test
It is possible for the algorithm to return an incorrect answer. If the input n is indeed prime, then the output will always correctly be probably prime. However, if the input n is composite then it is possible for the output to be incorrectly probably prime. The number n is then called a pseudoprimePseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
.
When n is odd and composite, at least half of all a with gcd(a,n) = 1 are Euler witnesses. We can prove this as follows: let {a1, a2, ..., am} be the Euler liars and a an Euler witness. Then, for i = 1,2,...,m:
Because the following holds:
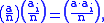
now we know that
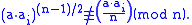
This gives that each ai gives a number a·ai, which is also an Euler witness.
So each Euler liar gives an Euler witness and so the number of Euler witnesses is larger or equal to the number of Euler liars. Therefore, when n is composite, at least half of all a with gcd(a,n) = 1 is an Euler witness.
Hence, the probability of failure is at most 2−k (compare this with the probability of failure for the Miller-Rabin primality test
Miller-Rabin primality test
The Miller–Rabin primality test or Rabin–Miller primality test is a primality test: an algorithmwhich determines whether a given number is prime,...
, which is at most 4−k).
For purposes of cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
the more bases a we test, i.e. if we pick a sufficiently large value of k, the better the accuracy of test. Hence the chance of the algorithm failing in this way is so small that the (pseudo) prime is used in practice in cryptographic applications, but for applications for which it is important to have a prime, a test like ECPP
Elliptic curve primality proving
Elliptic Curve Primality Proving is a method based on elliptic curves to prove the primality of a number . It is a general-purpose algorithm, meaning it does not depend on the number being of a special form...
or Pocklington should be used which proves primality.
Average-case behaviour
The bound 1/2 on the error probability of a single round of the Solovay–Strassen test holds for any input n, but those numbers n for which the bound is (approximately) attained are extremely rare. On the average, the error probability of the algorithm is significantly smaller: it is less than
for k rounds of the test, applied to uniformly random . The same bound also applies to the related problem of what is the conditional probability of n being composite for a random number which has been declared prime in k rounds of the test.
Complexity
The Solovay–Strassen algorithm shows that the decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
COMPOSITE is in the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
RP
RP (complexity)
In complexity theory, RP is the complexity class of problems for which a probabilistic Turing machine exists with these properties:* It always runs in polynomial time in the input size...
.