
1729 (number)
Encyclopedia
| 1729 | |
|---|---|
| Cardinal Cardinal number In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite... |
One thousand seven hundred [and] twenty-nine |
| Ordinal Ordinal number In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals... |
1729th |
| Factorization Factorization In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original... |
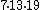 |
| Divisor Divisor In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:... s |
1, 7, 13, 19, 91, 133, 247, 1729 |
| Roman numeral | MDCCXXIX |
| Binary Binary numeral system The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2... |
11011000001 |
| Octal Octal The octal numeral system, or oct for short, is the base-8 number system, and uses the digits 0 to 7. Numerals can be made from binary numerals by grouping consecutive binary digits into groups of three... |
3301 |
| Duodecimal Duodecimal The duodecimal system is a positional notation numeral system using twelve as its base. In this system, the number ten may be written as 'A', 'T' or 'X', and the number eleven as 'B' or 'E'... |
1001 |
| Hexadecimal Hexadecimal In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen... |
6C1 |
1729 is the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
following 1728
1728 (number)
1728 is the natural number following 1727 and preceding 1729. 1728 is a dozen gross, one great gross .-In mathematics:...
and preceding 1730.
1729 is known as the Hardy–Ramanujan number after a famous anecdote of the British mathematician G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
regarding a hospital visit to the Indian mathematician Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
. In Hardy's words:
The two different ways are these:
- 1729 = 13 + 123 = 93 + 103
The quotation is sometimes expressed using the term "positive cubes", since allowing negative perfect cubes (the cube of a negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
) gives the smallest solution as 91
91 (number)
91 is the natural number following 90 and preceding 92.-In mathematics:Ninety-one is the twenty-seventh distinct semiprime and the second of the form...
(which is a divisor of 1729):
- 91 = 63 + (−5)3 = 43 + 33
Of course, equating "smallest" with "most negative", as opposed to "closest to zero" gives rise to solutions like −91, −189, −1729, and further negative numbers. This ambiguity is eliminated by the term "positive cubes".
Numbers that are the smallest number that can be expressed as the sum of two cubes in n distinct ways have been dubbed "taxicab number
Taxicab number
In mathematics, the nth taxicab number, typically denoted Ta or Taxicab, is defined as the smallest number that can be expressed as a sum of two positive algebraic cubes in n distinct ways. The concept was first mentioned in 1657 by Bernard Frénicle de Bessy, and was made famous in the early 20th...
s". The number was also found in one of Ramanujan's notebooks dated years before the incident, and was noted by Frenicle de Bessy in 1657.
The same expression defines 1729 as the first in the sequence of "Fermat near misses" defined as numbers of the form 1 + z3 which are also expressible as the sum of two other cubes.
1729 is also the third Carmichael number and the first absolute Euler pseudoprime
Euler pseudoprime
In arithmetic, an odd composite integer n is called an Euler pseudoprime to base a, if a and n are coprime, and....
. It is also a sphenic number
Sphenic number
In number theory, a sphenic number is a positive integer which is the product of three distinct prime numbers.Note that this definition is more stringent than simply requiring the integer to have exactly three prime factors; e.g. 60 = 22 × 3 × 5 has exactly 3 prime factors, but is not sphenic.All...
.
1729 is a Zeisel number. It is a centered cube number
Centered cube number
A centered cube number is a centered figurate number that represents a cube. The centered cube number for n is given byn^3 + ^3.The first few centered cube numbers are...
, as well as a dodecagonal number, a 24-gonal
Polygonal number
In mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots were thought of as alphas . These are one type of 2-dimensional figurate numbers.- Definition and examples :...
and 84-gonal number.
Investigating pairs of distinct integer-valued quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s that represent every integer the same number of times, Schiemann found that such quadratic forms must be in four or more variables, and the least possible discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of a four-variable pair is 1729 (Guy 2004).
Because in base 10 the number 1729 is divisible by the sum of its digits, it is a Harshad number
Harshad number
A Harshad number, or Niven number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "Harshad" comes from the Sanskrit + , meaning joy-giver. The Niven...
. It also has this property in octal
Octal
The octal numeral system, or oct for short, is the base-8 number system, and uses the digits 0 to 7. Numerals can be made from binary numerals by grouping consecutive binary digits into groups of three...
(1729 = 33018, 3 + 3 + 0 + 1 = 7) and hexadecimal
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
(1729 = 6C116, 6 + C + 1 = 1910), but not in binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
.
1729 has another mildly interesting property: the 1729th decimal place is the beginning of the first occurrence of all ten digits consecutively in the decimal representation of the transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
.
Masahiko Fujiwara
Masahiko Fujiwara
Masahiko Fujiwara is a Japanese mathematician, who is best known as an essayist....
showed that 1729 is one of four positive integers (with the others being 81
81 (number)
81 is the natural number following 80 and preceding 82.-In mathematics:Eighty-one is the square of 9 and the fourth power of 3. Like all powers of three, 81 is a perfect totient number. It is a heptagonal number and a centered octagonal number. It is also a tribonacci number, and an open meandric...
, 1458
1458 (number)
1458 is the integer after 1457 and before 1459.The maximum determinant of an 11 by 11 matrix of zeroes and ones is 1458.1458 is one of three numbers which, when its base 10 digits are added together, produces a sum which, when multiplied by its reversed self, yields the original number:The only...
, and the trivial case 1) which, when its digits are added together, produces a sum which, when multiplied by its reversal, yields the original number:
- 1 + 7 + 2 + 9 = 19
- 19 × 91 = 1729
It suffices only to check sums congruent to 0 or 1 (mod 9) up to 19.
Quotation
- "Every positive integer is one of Ramanujan's personal friends."—J. E. Littlewood, upon hearing of the taxicab incident.
See also
- Taxicab numberTaxicab numberIn mathematics, the nth taxicab number, typically denoted Ta or Taxicab, is defined as the smallest number that can be expressed as a sum of two positive algebraic cubes in n distinct ways. The concept was first mentioned in 1657 by Bernard Frénicle de Bessy, and was made famous in the early 20th...
- Interesting number paradoxInteresting number paradoxThe interesting number paradox is a semi-humorous paradox that arises from attempting to classify natural numbers as "interesting" or "dull". The paradox states that all natural numbers are interesting...
- Berry paradoxBerry paradoxThe Berry paradox is a self-referential paradox arising from the expression "the smallest possible integer not definable by a given number of words". Bertrand Russell, the first to discuss the paradox in print, attributed it to G. G...
- A Disappearing NumberA Disappearing NumberA Disappearing Number is a 2007 play co-written and devised by the Théâtre de Complicité company and directed and conceived by English playwright Simon McBurney. It was inspired by the collaboration during the 1910s between two of the most remarkable pure mathematicians of the twentieth century,...
, a 2007 play about Ramanujan in England during World War I.

