Discriminant
Encyclopedia
In algebra
, the discriminant of a polynomial
is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomial
is
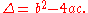
Here, if Δ > 0, the polynomial has two real roots, if Δ = 0, the polynomial has one real root, and if Δ < 0, the polynomial has no real roots. The discriminant of the cubic polynomial
is
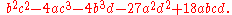
The discriminants of higher degree polynomials are significantly longer: the discriminant of a quartic
has 16 terms, that of a quintic has 59 terms, and that of a 6th degree polynomial has 246 terms.
A polynomial has a multiple root (i.e. a root with multiplicity
greater than one) in the complex numbers if and only if its discriminant is zero.
The concept also applies if the polynomial has coefficients in a field
which is not contained in the complex numbers. In this case, the discriminant vanishes if and only if the polynomial has a multiple root in its splitting field
.
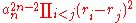
where
is the leading coefficient and 
are the roots (counting multiplicity
) of the polynomial in some splitting field. It is the square of the Vandermonde polynomial times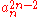
.
As the discriminant is a symmetric function in the roots, it can also be expressed in terms of the coefficients of the polynomial, since the coefficients are the elementary symmetric polynomial
s in the roots; such a formula is given below.
Expressing the discriminant in terms of the roots makes its key property clear, namely that it vanishes if and only if there is a repeated root, but does not allow it to be calculated without factoring a polynomial, after which the information it provides is redundant (if one has the roots, one can tell if there are any duplicates). Hence the formula in terms of the coefficients allows the nature of the roots to be determined without factoring the polynomial.
s, quadratic form
s, and algebraic number fields
. Discriminants in algebraic number theory
are closely related, and contain information about ramification
. In fact, the more geometric types of ramification are also related to more abstract types of discriminant, making this a central algebraic idea in many applications.
has discriminant
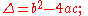
the cubic polynomial
has discriminant
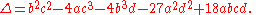
These are homogeneous polynomials in the coefficients, respectively of degree 2 and 4. Simpler polynomials have simpler expressions for their discriminants. For example, the monic quadratic polynomial
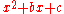
has discriminant
the monic cubic polynomial
has discriminant
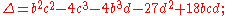
the monic cubic polynomial without quadratic term
has discriminant
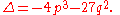
In terms of the roots, these are homogeneous polynomials of degree 2 (quadratic) and 6 (cubic).
in the coefficients; for monic polynomials, it is a homogeneous polynomial in the roots.
In the coefficients, the discriminant is homogeneous of degree
; this can be seen two ways.
In terms of the roots-and-leading-term formula, multiplying all the coefficients by
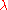does not change the roots, but multiplies the leading term by
. In terms of the formula as a determinant of a 
matrix divided by 
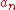, the determinant of the matrix is homogeneous of degree 
in the entries, and dividing by 
makes the degree 
; explicitly,
multiplying the coefficients by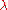
multiplies all entries of the matrix by 
, hence multiplies the determinant by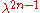 
.
For a monic polynomial, the discriminant is a polynomial in the roots alone (as the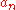
term is one), and is of degree 
in the roots, as there are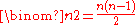 
terms in the product, each squared.
These are connected as the coefficients are elementary symmetric polynomials in the roots (hence individually homogeneous).
This description restricts the possible terms in the discriminant – each term consists of
coefficients, with total degree (as symmetric polynomials in the roots)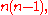 
with each coefficient having degree at most n. These thus correspond to partitions
of
into at most 
(positive) parts of size at most n. For the quadratic, these are partitions of 2 into at most 2 parts of size at most 2: 
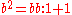and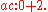 
For the cubic, these are partitions of 6 into at most 4 parts of size at most 3, all of which occur: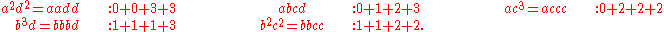
While this approach gives the possible terms, it does not determine the coefficients.
P(x) = ax2 + bx + c has discriminant Δ = b2 − 4ac, which is the quantity under the square root sign in the quadratic formula. For real numbers a, b, c, one has:
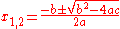
and its graph crosses the x-axis twice.
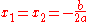
and its graph is tangent to the x-axis.
An alternative way to understand the discriminant of a quadratic is to use the characterization as "vanishes if and only if the polynomial has a repeated root".
In that case the polynomial is
The coefficients then satisfy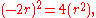
so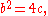 
and a monic quadratic has a repeated root if and only if this is the case, in which case the root is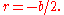
Putting both terms on one side and including a leading coefficient yields 
Since a polynomial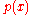
has a repeated root if and only if it shares a root with its derivative 
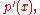the discriminant 
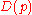and the resultant 
both have the property that they vanish if and only if p has a repeated root, and they have almost the same degree (the degree of the resultant is one greater than the degree of the discriminant) and thus are equal up to a factor of degree one.
The benefit of the resultant is that it can be computed as a determinant
, namely as the determinant of the Sylvester matrix
, a (2n − 1)×(2n − 1) matrix.
The resultant
of the general polynomial
is, up to a factor, equal to the determinant of the (2n − 1)×(2n − 1) Sylvester matrix: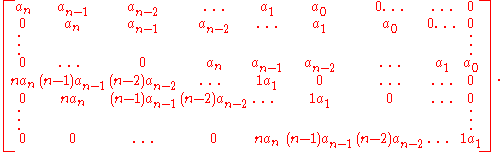
The discriminant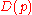
of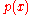 
is now given by the formula
For example, in the case n = 4, the above determinant is
The discriminant of the degree 4 polynomial is then obtained from this determinant upon dividing by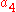
.
In terms of the roots, the discriminant is equal to
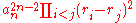
where r1, ..., rn are the complex
roots (counting multiplicity
) of the polynomial p(x):
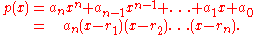
This second expression makes it clear that p has a multiple root if and only if
the discriminant is zero. (This multiple root can be complex.)
The discriminant can be defined for polynomials over arbitrary field
s, in exactly the same fashion as above. The product formula involving the roots ri remains valid; the roots have to be taken in some splitting field
of the polynomial. The discriminant can even be defined for polynomials over any commutative ring
. However, if the ring is not an integral domain, above division of the resultant by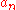
should be replaced by substituting 
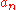by 1 in the first column of the matrix.
Thus in particular for a quadratic polynomial with real coefficients, a real number has real square roots if and only if it is nonnegative, and these roots are distinct if and only if it is positive (not zero). Thus
Further, for a quadratic polynomial with rational coefficients, it factors over the rationals if and only the if the discriminant – which is necessarily a rational number, being a polynomial in the coefficients – is in fact a square.
To decide if a polynomial has a triple root or not, one may compute the discriminant of a cubic and the discriminant of its derivative – it has a triple root if and only if both of these vanish; equivalently, if and only if the resultants
and 
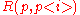(or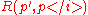 
) vanish. Note that two polynomials are required, because the set of cubics with a triple root is a codimension
2 subvariety of the projective space
of all cubics, and thus by dimension counting one needs two polynomials to determine this set. More directly, there is a 1-parameter set of cubics with a triple root – the parameter being the root – while there is a 3-parameter set of cubics with possibly different roots. Explicitly, the cubics with a triple root are given parametrically as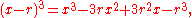
so the coefficients are 
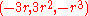– up to scale, the twisted cubic
.
. However, as the division is not always defined in such a ring, instead of dividing the determinant by the leading coefficient, one substitutes the leading coefficient by 1 in the first column of the determinant. This generalized discriminant has the following property which is fundamental in algebraic geometry
.
Let f be a polynomial with coefficients in a commutative ring A and D its discriminant. Let φ be a ring homomorphism
of A into a field K and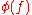
be the polynomial over K obtained by replacing the coefficients of f by their images by φ. Then 
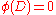if and only if either the difference of the degrees of f and 
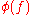is at least 2 or 
has a multiple root in an algebraic closure
of K. The first case may be interpreted by saying that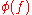
has a multiple root at infinity.
The typical situation where this property is applied is when A is a (univariate or multivariate) polynomial ring over a field k and φ is the substitution of the indeterminates in A by elements of a field extension
K of k.
For example, let f be a bivariate polynomial in X and Y with real coefficients, such that f=0 is the implicit equation of a plane algebraic curve
. Viewing f as a univariate polynomial in Y with coefficients depending on X, then the discriminant is a polynomial in X whose roots are the X-coordinates of the singular points, of the points with a tangent parallel to the Y-axis and of some of the asymptotes parallel to the Y-axis. In other words the computation of the roots of the Y-discriminant and the X-discriminant allows to compute all remarkable points of the curve, except the inflection point
s.
defined in plane geometry by the real polynomial
the discriminant is equal to
and determines the shape
of the conic section. If the discriminant is less than 0, the equation is of an ellipse
or a circle
. If the discriminant equals 0, the equation is that of a parabola
. If the discriminant is greater than 0, the equation is that of a hyperbola
. This formula will not work for degenerate cases (when the polynomial factors).
s Q over any field
K of characteristic
≠ 2.
Given a quadratic form Q, the discriminant is the determinant of a symmetric matrix S for Q.
Change of variables by a matrix A changes the matrix of the symmetric form by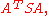
which has determinant 
so under change of variables, the discriminant changes by a non-zero square, and thus the class of the discriminant is well-defined in K/(K*)2, i.e., up to non-zero squares. See also quadratic residue.
Less intrinsically, by a theorem of Jacobi quadratic forms on
can be expressed in diagonal form as
or more generally quadratic forms on V as a sum
where the Li are linear forms and 1 ≤ i ≤ n where n is the number of variables. Then the discriminant is the product of the ai, which is well-defined as a class in K/(K*)2.
For K=R, the real numbers, (R*)2 is the positive real numbers (any positive number is a square of a non-zero number), and thus the quotient R/(R*)2 has three elements: positive, zero, and negative.
For K=C, the complex numbers, (C*)2 is the non-zero complex numbers (any complex number is a square), and thus the quotient C/(C*)2 has two elements: non-zero and zero.
This definition generalizes the discriminant of a quadratic polynomial, as the polynomial
homogenizes to the quadratic form 
which has symmetric matrix
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the discriminant of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomial
is
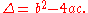
Here, if Δ > 0, the polynomial has two real roots, if Δ = 0, the polynomial has one real root, and if Δ < 0, the polynomial has no real roots. The discriminant of the cubic polynomial
is
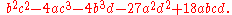
The discriminants of higher degree polynomials are significantly longer: the discriminant of a quartic
Quartic function
In mathematics, a quartic function, or equation of the fourth degree, is a function of the formf=ax^4+bx^3+cx^2+dx+e \,where a is nonzero; or in other words, a polynomial of degree four...
has 16 terms, that of a quintic has 59 terms, and that of a 6th degree polynomial has 246 terms.
A polynomial has a multiple root (i.e. a root with multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
greater than one) in the complex numbers if and only if its discriminant is zero.
The concept also applies if the polynomial has coefficients in a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
which is not contained in the complex numbers. In this case, the discriminant vanishes if and only if the polynomial has a multiple root in its splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
.
Formula
In terms of the roots, the discriminant is given by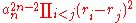where
is the leading coefficient and are the roots (counting multiplicityMultiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
) of the polynomial in some splitting field. It is the square of the Vandermonde polynomial times
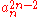.As the discriminant is a symmetric function in the roots, it can also be expressed in terms of the coefficients of the polynomial, since the coefficients are the elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s in the roots; such a formula is given below.
Expressing the discriminant in terms of the roots makes its key property clear, namely that it vanishes if and only if there is a repeated root, but does not allow it to be calculated without factoring a polynomial, after which the information it provides is redundant (if one has the roots, one can tell if there are any duplicates). Hence the formula in terms of the coefficients allows the nature of the roots to be determined without factoring the polynomial.
Generalizations
The concept of discriminant has been generalized to other algebraic structures besides polynomials of one variable, including conic sectionConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s, quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s, and algebraic number fields
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
. Discriminants in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
are closely related, and contain information about ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
. In fact, the more geometric types of ramification are also related to more abstract types of discriminant, making this a central algebraic idea in many applications.
Formula
The quadratic polynomialhas discriminant
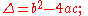
the cubic polynomial
has discriminant
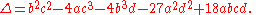
These are homogeneous polynomials in the coefficients, respectively of degree 2 and 4. Simpler polynomials have simpler expressions for their discriminants. For example, the monic quadratic polynomial
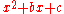
has discriminant
the monic cubic polynomial
has discriminant
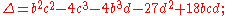
the monic cubic polynomial without quadratic term
has discriminant
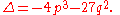
In terms of the roots, these are homogeneous polynomials of degree 2 (quadratic) and 6 (cubic).
Homogeneity
The discriminant is a homogeneous polynomialHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
in the coefficients; for monic polynomials, it is a homogeneous polynomial in the roots.
In the coefficients, the discriminant is homogeneous of degree
; this can be seen two ways.In terms of the roots-and-leading-term formula, multiplying all the coefficients by
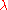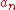does not change the roots, but multiplies the leading term by. In terms of the formula as a determinant of a matrix divided by , the determinant of the matrix is homogeneous of degree in the entries, and dividing by makes the degree ; explicitly,multiplying the coefficients by
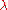multiplies all entries of the matrix by , hence multiplies the determinant by 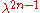.For a monic polynomial, the discriminant is a polynomial in the roots alone (as the
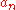term is one), and is of degree in the roots, as there are 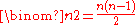terms in the product, each squared.These are connected as the coefficients are elementary symmetric polynomials in the roots (hence individually homogeneous).
This description restricts the possible terms in the discriminant – each term consists of
coefficients, with total degree (as symmetric polynomials in the roots) 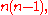with each coefficient having degree at most n. These thus correspond to partitionsPartition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of
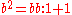into at most (positive) parts of size at most n. For the quadratic, these are partitions of 2 into at most 2 parts of size at most 2: and 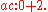For the cubic, these are partitions of 6 into at most 4 parts of size at most 3, all of which occur:
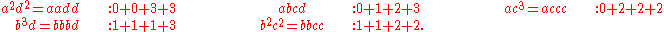
While this approach gives the possible terms, it does not determine the coefficients.
Quadratic formula
The quadratic polynomialQuadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
P(x) = ax2 + bx + c has discriminant Δ = b2 − 4ac, which is the quantity under the square root sign in the quadratic formula. For real numbers a, b, c, one has:
- When Δ > 0 , P(x) has two distinct real roots
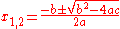
and its graph crosses the x-axis twice.
- When Δ = 0, P(x) has two coincident real roots
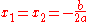
and its graph is tangent to the x-axis.
- When Δ < 0 , P(x) has no real roots, and its graph lies strictly above or below the x-axis.
An alternative way to understand the discriminant of a quadratic is to use the characterization as "vanishes if and only if the polynomial has a repeated root".
In that case the polynomial is
The coefficients then satisfy
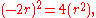so 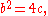and a monic quadratic has a repeated root if and only if this is the case, in which case the root is
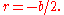Putting both terms on one side and including a leading coefficient yields Discriminant of a polynomial
To find the formula for the discriminant of a polynomial in terms of its coefficients, it is easiest to introduce the resultant. Just as the discriminant of a single polynomial is the product of the squares of the difference between the distinct roots of a polynomial, the resultant of two polynomials is the product of the differences between their roots, and just as the discriminant vanishes if and only if the polynomial has a repeated root, the resultant vanishes if and only if the two polynomials share a root.Since a polynomial
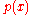has a repeated root if and only if it shares a root with its derivative 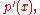the discriminant 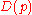and the resultant both have the property that they vanish if and only if p has a repeated root, and they have almost the same degree (the degree of the resultant is one greater than the degree of the discriminant) and thus are equal up to a factor of degree one.The benefit of the resultant is that it can be computed as a determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
, namely as the determinant of the Sylvester matrix
Sylvester matrix
In mathematics, a Sylvester matrix is a matrix associated to two polynomials that provides information about those polynomials. It is named for James Joseph Sylvester.-Definition:...
, a (2n − 1)×(2n − 1) matrix.
The resultant
of the general polynomialis, up to a factor, equal to the determinant of the (2n − 1)×(2n − 1) Sylvester matrix:
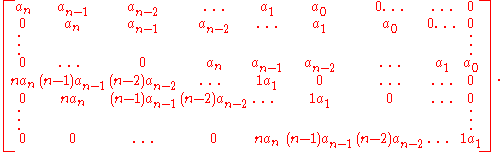
The discriminant
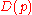of 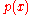is now given by the formulaFor example, in the case n = 4, the above determinant is
The discriminant of the degree 4 polynomial is then obtained from this determinant upon dividing by
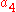.In terms of the roots, the discriminant is equal to
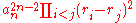
where r1, ..., rn are the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
roots (counting multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
) of the polynomial p(x):
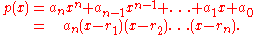
This second expression makes it clear that p has a multiple root if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the discriminant is zero. (This multiple root can be complex.)
The discriminant can be defined for polynomials over arbitrary field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s, in exactly the same fashion as above. The product formula involving the roots ri remains valid; the roots have to be taken in some splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of the polynomial. The discriminant can even be defined for polynomials over any commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. However, if the ring is not an integral domain, above division of the resultant by
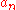should be replaced by substituting 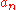by 1 in the first column of the matrix.Nature of the roots
The discriminant gives additional information on the nature of the roots beyond simply whether there are any repeated roots: it also gives information on whether the roots are real or complex, and rational or irrational. More formally, it gives information on whether the roots are in the field over which the polynomial is defined, or are in an extension field, and hence whether the polynomial factors over the field of coefficients. This is most transparent and easily stated for quadratic and cubic polynomials; for polynomials of degree 4 or higher this is more difficult to state.Quadratic
Because the quadratic formula expressed the roots of a quadratic polynomial as a rational function in terms of the square root of the discriminant, the roots of a quadratic polynomial are in the same field as the coefficients if and only if the discriminant is a square in the field of coefficients: in other words, the polynomial factors over the field of coefficients if and only if the discriminant is a square.Thus in particular for a quadratic polynomial with real coefficients, a real number has real square roots if and only if it is nonnegative, and these roots are distinct if and only if it is positive (not zero). Thus
- Δ > 0: 2 distinct real roots: factors over the reals;
- Δ < 0: 2 distinct complex roots (complex conjugate), does not factor over the reals;
- Δ = 0: 1 real root with multiplicityMultiplicity (mathematics)In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
2: factors over the reals as a square.
Further, for a quadratic polynomial with rational coefficients, it factors over the rationals if and only the if the discriminant – which is necessarily a rational number, being a polynomial in the coefficients – is in fact a square.
Cubic
For a cubic polynomial with real coefficients, the discriminant reflects the nature of the roots as follows:- Δ > 0: the equation has 3 distinct real roots;
- Δ < 0, the equation has 1 real root and 2 complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
roots; - Δ = 0: at least 2 roots coincide, and they are all real.
- It may be that the equation has a double real root and another distinct single real root; alternatively, all three roots coincide yielding a triple real root.
To decide if a polynomial has a triple root or not, one may compute the discriminant of a cubic and the discriminant of its derivative – it has a triple root if and only if both of these vanish; equivalently, if and only if the resultants
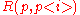and (or 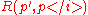) vanish. Note that two polynomials are required, because the set of cubics with a triple root is a codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
2 subvariety of the projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
of all cubics, and thus by dimension counting one needs two polynomials to determine this set. More directly, there is a 1-parameter set of cubics with a triple root – the parameter being the root – while there is a 3-parameter set of cubics with possibly different roots. Explicitly, the cubics with a triple root are given parametrically as
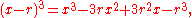so the coefficients are 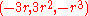– up to scale, the twisted cubicTwisted cubic
In mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation...
.
Discriminant of a polynomial over a commutative ring
The definition of the discriminant of a polynomial in terms of the resultant may easily be extended to polynomials whose coefficients belong to any commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. However, as the division is not always defined in such a ring, instead of dividing the determinant by the leading coefficient, one substitutes the leading coefficient by 1 in the first column of the determinant. This generalized discriminant has the following property which is fundamental in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Let f be a polynomial with coefficients in a commutative ring A and D its discriminant. Let φ be a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
of A into a field K and
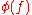be the polynomial over K obtained by replacing the coefficients of f by their images by φ. Then 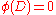if and only if either the difference of the degrees of f and 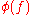is at least 2 or has a multiple root in an algebraic closureAlgebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of K. The first case may be interpreted by saying that
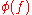has a multiple root at infinity.The typical situation where this property is applied is when A is a (univariate or multivariate) polynomial ring over a field k and φ is the substitution of the indeterminates in A by elements of a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
K of k.
For example, let f be a bivariate polynomial in X and Y with real coefficients, such that f=0 is the implicit equation of a plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
. Viewing f as a univariate polynomial in Y with coefficients depending on X, then the discriminant is a polynomial in X whose roots are the X-coordinates of the singular points, of the points with a tangent parallel to the Y-axis and of some of the asymptotes parallel to the Y-axis. In other words the computation of the roots of the Y-discriminant and the X-discriminant allows to compute all remarkable points of the curve, except the inflection point
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
s.
Discriminant of a conic section
For a conic sectionConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
defined in plane geometry by the real polynomial
the discriminant is equal to
and determines the shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
of the conic section. If the discriminant is less than 0, the equation is of an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
or a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. If the discriminant equals 0, the equation is that of a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. If the discriminant is greater than 0, the equation is that of a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. This formula will not work for degenerate cases (when the polynomial factors).
Discriminant of a quadratic form
There is a substantive generalization to quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s Q over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
≠ 2.
Given a quadratic form Q, the discriminant is the determinant of a symmetric matrix S for Q.
Change of variables by a matrix A changes the matrix of the symmetric form by
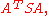which has determinant so under change of variables, the discriminant changes by a non-zero square, and thus the class of the discriminant is well-defined in K/(K*)2, i.e., up to non-zero squares. See also quadratic residue.Less intrinsically, by a theorem of Jacobi quadratic forms on
can be expressed in diagonal form asor more generally quadratic forms on V as a sum
where the Li are linear forms and 1 ≤ i ≤ n where n is the number of variables. Then the discriminant is the product of the ai, which is well-defined as a class in K/(K*)2.
For K=R, the real numbers, (R*)2 is the positive real numbers (any positive number is a square of a non-zero number), and thus the quotient R/(R*)2 has three elements: positive, zero, and negative.
For K=C, the complex numbers, (C*)2 is the non-zero complex numbers (any complex number is a square), and thus the quotient C/(C*)2 has two elements: non-zero and zero.
This definition generalizes the discriminant of a quadratic polynomial, as the polynomial
homogenizes to the quadratic form which has symmetric matrix
-
whose determinant is
Up to a factor of -4, this is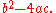 
The invariance of the class of the discriminant of a real form (positive, zero, or negative) corresponds to the corresponding conic section being an ellipse, parabola, or hyperbola.
Discriminant of a differentiable function
In differential topology, the discriminant of a differentiable function f is the same as the set of critical values of f. The discriminant in this sense is somewhat related to the discriminant of a polynomial; for example, if f(x)=ax2+bx+c is a quadratic (a≠0), then the critical value of f will be
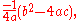which is (up to a constant) equal to the discriminant of a quadratic polynomial.
Alternating polynomials
The discriminant is a symmetric polynomialSymmetric polynomialIn mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
in the roots; if one adjoins a square root of it (halves each of the powers: the Vandermonde polynomial) to the ring of symmetric polynomials in n variables
, one obtains the ring of alternating polynomials, which is thus a quadratic extension of 
.
External links