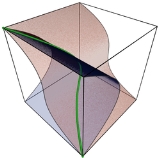
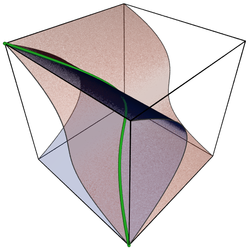
Twisted cubic
Encyclopedia
In mathematics
, a twisted cubic is a smooth, rational curve C of degree
three in projective 3-space
P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation (the twisted cubic, therefore). It is generally considered to be the simplest example of a projective variety that isn't linear or a hypersurface
, and is given as such in most textbooks on algebraic geometry
. It is the three-dimensional case of the rational normal curve, and is the image of a Veronese map of degree three on the projective line.
 It is most easily given parametrically as the image of the map
It is most easily given parametrically as the image of the map
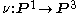
which assigns to the homogeneous coordinate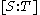 the value
the value
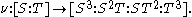
In one coordinate patch of projective space, the map is simply
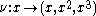
That is, it is the closure by a single point at infinity of the affine curve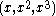 .
.
Equivalently, it is a projective variety, defined as the zero locus of three smooth quadric
s. Given the homogeneous coordinates [X:Y:Z:W] on P3, it is the zero locus of the three homogeneous polynomial
s
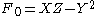
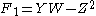
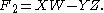
It may be checked that these three quadratic form
s vanish identically when using the explicit parameterization above; that is, substituting S3 for X, and so on.
In fact, the homogeneous ideal of the twisted cubic C is generated by three algebraic forms of degree two on P3. The generators of the ideal are
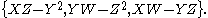
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a twisted cubic is a smooth, rational curve C of degree
Degree of an algebraic variety
The degree of an algebraic variety in mathematics is defined, for a projective variety V, by an elementary use of intersection theory.For V embedded in a projective space Pn and defined over some algebraically closed field K, the degree d of V is the number of points of intersection of V, defined...
three in projective 3-space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation (the twisted cubic, therefore). It is generally considered to be the simplest example of a projective variety that isn't linear or a hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
, and is given as such in most textbooks on algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. It is the three-dimensional case of the rational normal curve, and is the image of a Veronese map of degree three on the projective line.
Definition

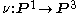
which assigns to the homogeneous coordinate
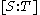 the value
the value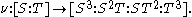
In one coordinate patch of projective space, the map is simply
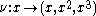
That is, it is the closure by a single point at infinity of the affine curve
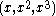 .
.Equivalently, it is a projective variety, defined as the zero locus of three smooth quadric
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
s. Given the homogeneous coordinates [X:Y:Z:W] on P3, it is the zero locus of the three homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s
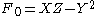
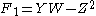
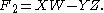
It may be checked that these three quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s vanish identically when using the explicit parameterization above; that is, substituting S3 for X, and so on.
In fact, the homogeneous ideal of the twisted cubic C is generated by three algebraic forms of degree two on P3. The generators of the ideal are
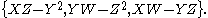
Properties
The twisted cubic has an assortment of elementary properties:- It is the set-theoretic complete intersection of XZ-Y2 and
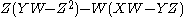 , but not a scheme-theoretic or ideal-theoretic complete intersection (the resulting ideal is not radical, since
, but not a scheme-theoretic or ideal-theoretic complete intersection (the resulting ideal is not radical, since 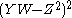 is in it, but
is in it, but 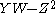 is not).
is not). - Any four points on C span P3.
- Given six points in P3 with no four coplanar, there is a unique twisted cubic passing through them.
- The union of the tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
and secantSecant lineA secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
lines, the secant variety, of a twisted cubic C fill up P3 and the lines are pairwise disjoint, except at points of the curve itself. In fact, the union of the tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
and secantSecant lineA secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
lines of any non-planar smooth algebraic curveAlgebraic curveIn algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
is three-dimensional. Further, any smooth algebraic varietyAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
with the property that every length four subscheme spans P3 has the property that the tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
and secantSecant lineA secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
lines are pairwise disjoint, except at points of the variety itself. - The projection of C onto a plane from a point on a tangent line of C yields a cuspidal cubic.
- The projection from a point on a secant line of C yields a nodal cubic.
- The projection from a point on C yields a conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
.

