
Degree of an algebraic variety
Encyclopedia
The degree of an algebraic variety in mathematics
is defined, for a projective variety V, by an elementary use of intersection theory
.
For V embedded in a projective space
Pn and defined over some algebraically closed field
K, the degree d of V is the number of points of intersection of V, defined over K, with a linear subspace
L in general position
, when
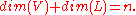
Here dim(V) is the dimension
of V, and the codimension
of L will be equal to that dimension. The degree d is an extrinsic quantity, and not intrinsic as a property of V. For example the projective line
has an (essentially unique) embedding of degree n in Pn.
The degree of a hypersurface
F = 0 is the same as the total degree
of the homogeneous polynomial
F defining it (granted, in case F has repeated factors, that intersection theory is used to count intersections with multiplicity, as in Bézout's theorem
).
For a more sophisticated approach, the linear system of divisors
defining the embedding of V can be related to the line bundle
or invertible sheaf
defining the embedding by its space of sections. The tautological line bundle
on Pn pulls back to V. The degree determines the first Chern class
. The degree can also be computed in the cohomology ring
of Pn, or Chow ring
, with the class of a hyperplane
intersecting the class of V an appropriate number of times.
The degree can be used to generalize Bézout's theorem in an expected way to intersections of n hypersurfaces in Pn.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
is defined, for a projective variety V, by an elementary use of intersection theory
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
.
For V embedded in a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Pn and defined over some algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
K, the degree d of V is the number of points of intersection of V, defined over K, with a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
L in general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
, when
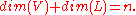
Here dim(V) is the dimension
Dimension of an algebraic variety
In mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
of V, and the codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
of L will be equal to that dimension. The degree d is an extrinsic quantity, and not intrinsic as a property of V. For example the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
has an (essentially unique) embedding of degree n in Pn.
The degree of a hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
F = 0 is the same as the total degree
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
of the homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
F defining it (granted, in case F has repeated factors, that intersection theory is used to count intersections with multiplicity, as in Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
).
For a more sophisticated approach, the linear system of divisors
Linear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
defining the embedding of V can be related to the line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
or invertible sheaf
Invertible sheaf
In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
defining the embedding by its space of sections. The tautological line bundle
Canonical line bundle
The canonical or tautological line bundle on a projective space appears frequently in mathematics, often in the study of characteristic classes...
on Pn pulls back to V. The degree determines the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
. The degree can also be computed in the cohomology ring
Cohomology ring
In mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
of Pn, or Chow ring
Chow ring
In algebraic geometry, the Chow ring of an algebraic variety is an algebraic-geometric analogue of the cohomology ring of the variety considered as a topological space: its elements are formed out of actual subvarieties and its multiplicative structure is derived from the intersection of...
, with the class of a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
intersecting the class of V an appropriate number of times.
The degree can be used to generalize Bézout's theorem in an expected way to intersections of n hypersurfaces in Pn.

