Canonical line bundle
Encyclopedia
The canonical or tautological line bundle
on a projective space
appears frequently in mathematics
, often in the study of characteristic class
es. Note that there is possible confusion with the theory of the canonical class in algebraic geometry
; for which reason the name tautological is preferred in some contexts.
For generalizations to Grassmannian
s, see also tautological bundle
.
, with the first factor denoting real projective n-space
. We consider the subset
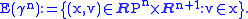
We have an obvious projection map
, with 
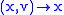. Each fibre
of
is then the line
inside Euclidean (n+1)-space
. Giving each fibre the induced vector space
structure we obtain the bundle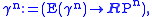
the canonical line bundle over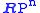
.
by either the complex numbers 
or the quaternions Thus we obtain the complex line bundle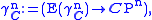
whose fibres are isomorphic to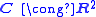
, and the quaternionic line bundle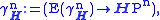
whose fibres are isomorphic to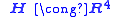
.
, this notion exists over any commutative unital ring.
Over a field, its dual line bundle is the line bundle associated to the hyperplane divisor H, whose global sections are the linear forms. Its Chern class is -H. This is an example of an anti-ample line bundle
.
In fact, it is straightforward to show that, for
, the real canonical line bundle is none other than the well-known bundle whose total space
is the Möbius strip
. For a full proof of the above fact, see.
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
on a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
appears frequently in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, often in the study of characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es. Note that there is possible confusion with the theory of the canonical class in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
; for which reason the name tautological is preferred in some contexts.
For generalizations to Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
s, see also tautological bundle
Tautological bundle
In mathematics, tautological bundle is a term for a particularly natural vector bundle occurring over a Grassmannian, and more specially over projective space...
.
Definition
Form the cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, with the first factor denoting real projective n-spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. We consider the subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
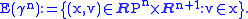
We have an obvious projection map
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
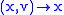, with . Each fibreFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
of
is then the lineLine (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
inside Euclidean (n+1)-spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Giving each fibre the induced vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
structure we obtain the bundle
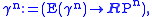
the canonical line bundle over
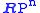.Complex and quaternionic cases
The above definition continues to makes sense if we replace the field by either the complex numbers or the quaternions Thus we obtain the complex line bundle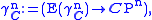whose fibres are isomorphic to
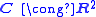, and the quaternionic line bundle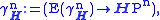whose fibres are isomorphic to
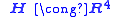.Tautological line bundle in algebraic geometry
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, this notion exists over any commutative unital ring.
Over a field, its dual line bundle is the line bundle associated to the hyperplane divisor H, whose global sections are the linear forms. Its Chern class is -H. This is an example of an anti-ample line bundle
Ample line bundle
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
.
Facts
is locally trivialFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
but not trivial, for
.
In fact, it is straightforward to show that, for
, the real canonical line bundle is none other than the well-known bundle whose total spaceFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
is the Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
. For a full proof of the above fact, see.