Splitting field
Encyclopedia
In abstract algebra
, a splitting field
of a polynomial
with coefficients in a field
is a smallest field extension
of that field over which the polynomial factors (or "splits", hence the name) into linear factors.
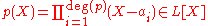
and such that the coefficients ai generate L over K. The extension L is then an extension of minimal degree
over K in which p splits. It can be shown that such splitting fields exist and are unique up to
isomorphism. The amount of freedom in that isomorphism is known to be the Galois group
of p (if we assume it is separable
).
Given an algebraically closed field
A containing K, there is a unique splitting field L of p between K and A, generated by the roots of p. If K is a subfield of the complex number
s, the existence is automatic. On the other hand, the existence of algebraic closures in general is usually proved by 'passing to the limit' from the splitting field result; which is therefore proved directly to avoid circular reasoning
.
Given a separable extension
K′ of K, a Galois closure L of K′ is a type of splitting field, and also a Galois extension
of K containing K′ that is minimal, in an obvious sense. Such a Galois closure should contain a splitting field for all the polynomials p over K that are minimal polynomials over K of elements a of K′.
over 
, the real numbers. By constructing the splitting field for such a polynomial one can find the roots of the polynomial in the new field.
F[X] of degree n. The general process for constructing K, the splitting field of p(X) over F, is to construct a sequence of fields
such that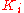 
is an extension of 
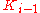containing a new root of p(X). Since p(X) has at most n roots the construction will require at most n extensions. The steps for constructing 
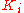are given as follows:
The irreducible factor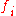
used in the quotient construction may be chosen arbitrarily. Although different choices of factors may lead to different subfield sequences the resulting splitting fields will be isomorphic.
Since f(X) is irreducible, (f(X)) is a maximal ideal
and hence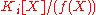
is, in fact, a field. Moreover, if we let 
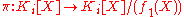be the natural projection of the ring onto its quotient then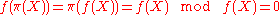
so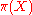
is a root of f(X) and of p(X).
The degree of a single extension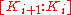
is equal to the degree of the irreducible factor f(X). The degree of the extension [K : F] is given by 
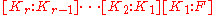and is at most n!.
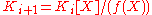is a field when f(X) is irreducible. Its elements are of the form 
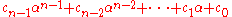where the 
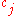are in 
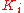and 
. (If one considers 
as a vector space over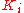 
then the powers 
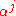for form a basis.)
The elements of
can be considered as polynomials in 
of degree less than n. Addition in 
is given by the rules for polynomial addition and multiplication is given by polynomial multiplication modulo f(X). That is, for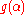 
and 
in 
the product 
where r(X) is the remainder of g(X)h(X) divided by f(X) in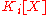 
.
The remainder r(X) can be computed through long division of polynomials, however there is also a straightforward reduction rule that can be used to compute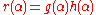
directly. First let 
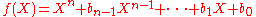. (The polynomial is over a field so one can take f(X) to be monic
without loss of generality.) Now α is a root of f(X), so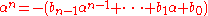
. If the product 
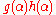has a term 
with it can be reduced as follows:
.
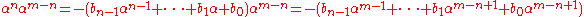As an example of the reduction rule, take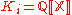
, the ring of polynomials with rational coefficients, and take 
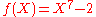. Let 
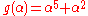and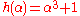 
be two elements of 
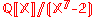. The reduction rule given by f(X) is 
so
R[x], and the irreducible polynomial
The quotient space
is given by the congruence
As a result, the elements (or equivalence classes) of are of the form where a and b belong to R. To see this, note that since it follows that , , , etc.; and so, for example
The addition and multiplication operations are given by firstly using ordinary polynomial addition and multiplication, but then reducing modulo , i.e. using the fact that , , , , etc. Thus: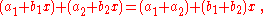
If we identify with (a,b) then we see that addition and multiplication are given by
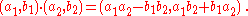
We claim that, as a field, the quotient is isomorphic to the complex number
s, C. A general complex number is of the form , where a and b are real numbers and Addition and multiplication are given by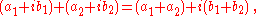
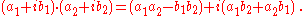
If we identify with (a,b) then we see that addition and multiplication are given by
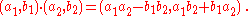
The previous calculations show that addition and multiplication behave the same way in and C. In fact, we see that the map between and C given by is a homomorphism
with respect to addition and multiplication. It is also obvious that the map is both injective and surjective; meaning that is a bijective homomorphism, i.e. an isomorphism. It follows that, as claimed:
then a splitting field L will contain a primitive cube root of unity, as well as a cube root of 2. Thus
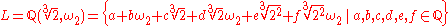
where
, 
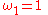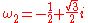, and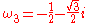
are the cubic roots of unity.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with coefficients in a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is a smallest field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of that field over which the polynomial factors (or "splits", hence the name) into linear factors.
Definition
A splitting field of a polynomial p(X) over a field K is a field extension L of K over which p factors into linear factors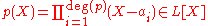and such that the coefficients ai generate L over K. The extension L is then an extension of minimal degree
Degree of a field extension
In mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
over K in which p splits. It can be shown that such splitting fields exist and are unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism. The amount of freedom in that isomorphism is known to be the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of p (if we assume it is separable
Separable polynomial
In mathematics, two slightly different notions of separable polynomial are used, by different authors.According to the most common one, a polynomial P over a given field K is separable if all its roots are distinct in an algebraic closure of K, that is the number of its distinct roots is equal to...
).
Facts
An extension L which is a splitting field for multiple polynomials p(X) over K is called a normal extension.Given an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
A containing K, there is a unique splitting field L of p between K and A, generated by the roots of p. If K is a subfield of the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, the existence is automatic. On the other hand, the existence of algebraic closures in general is usually proved by 'passing to the limit' from the splitting field result; which is therefore proved directly to avoid circular reasoning
Circular definition
A circular definition is one that uses the term being defined as a part of the definition or assumes a prior understanding of the term being defined. Either the audience must already know the meaning of the key term, or the definition is deficient in including the term to be defined in the...
.
Given a separable extension
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
K′ of K, a Galois closure L of K′ is a type of splitting field, and also a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of K containing K′ that is minimal, in an obvious sense. Such a Galois closure should contain a splitting field for all the polynomials p over K that are minimal polynomials over K of elements a of K′.
Motivation
Finding roots of polynomials has been an important problem since the time of the ancient Greeks. Some polynomials, however, have no roots such as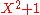 over , the real numbers. By constructing the splitting field for such a polynomial one can find the roots of the polynomial in the new field.The Construction
Let F be a field and p(X) be a polynomial in the polynomial ringPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
F[X] of degree n. The general process for constructing K, the splitting field of p(X) over F, is to construct a sequence of fields
such that 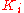is an extension of 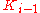containing a new root of p(X). Since p(X) has at most n roots the construction will require at most n extensions. The steps for constructing 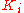are given as follows:- Factorize p(X) over
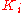into irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
factors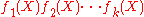
. - Choose any nonlinear irreducible factor
. - Construct the field extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of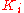 
as the quotient ringQuotient ringIn ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
where (f(X)) denotes the idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in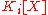
generated by f(X) - Repeat the process for
until p(X) completely factors.
The irreducible factor
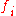used in the quotient construction may be chosen arbitrarily. Although different choices of factors may lead to different subfield sequences the resulting splitting fields will be isomorphic.Since f(X) is irreducible, (f(X)) is a maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
and hence
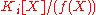is, in fact, a field. Moreover, if we let 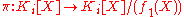be the natural projection of the ring onto its quotient then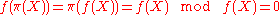so
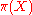is a root of f(X) and of p(X).The degree of a single extension
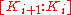is equal to the degree of the irreducible factor f(X). The degree of the extension [K : F] is given by 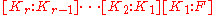and is at most n!.The Field Ki[x]/(ƒ(x))
As mentioned above, the quotient ring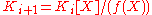 is a field when f(X) is irreducible. Its elements are of the form 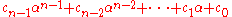where the 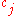are in 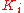and . (If one considers as a vector space over 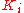then the powers 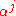for form a basis.)The elements of
can be considered as polynomials in of degree less than n. Addition in is given by the rules for polynomial addition and multiplication is given by polynomial multiplication modulo f(X). That is, for 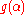and in the product where r(X) is the remainder of g(X)h(X) divided by f(X) in 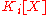.The remainder r(X) can be computed through long division of polynomials, however there is also a straightforward reduction rule that can be used to compute
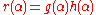directly. First let 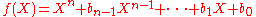. (The polynomial is over a field so one can take f(X) to be monicMonic
In mathematics, monic can refer to*monic morphism - a special kind of morphism in category theory.*monic polynomial - a polynomial whose leading coefficient is one.In linguistics, monic can refer to*Monic languages...
without loss of generality.) Now α is a root of f(X), so
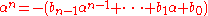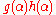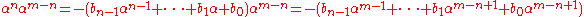. If the product has a term with it can be reduced as follows:.As an example of the reduction rule, take
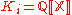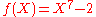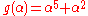, the ring of polynomials with rational coefficients, and take . Let and 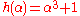be two elements of 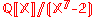. The reduction rule given by f(X) is soThe complex numbers
Consider the polynomial ringPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[x], and the irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
The quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
is given by the congruence
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
As a result, the elements (or equivalence classes) of are of the form where a and b belong to R. To see this, note that since it follows that , , , etc.; and so, for example
The addition and multiplication operations are given by firstly using ordinary polynomial addition and multiplication, but then reducing modulo , i.e. using the fact that , , , , etc. Thus:
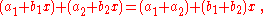
If we identify with (a,b) then we see that addition and multiplication are given by
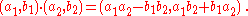
We claim that, as a field, the quotient is isomorphic to the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, C. A general complex number is of the form , where a and b are real numbers and Addition and multiplication are given by
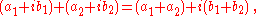
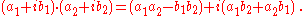
If we identify with (a,b) then we see that addition and multiplication are given by
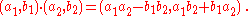
The previous calculations show that addition and multiplication behave the same way in and C. In fact, we see that the map between and C given by is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
with respect to addition and multiplication. It is also obvious that the map is both injective and surjective; meaning that is a bijective homomorphism, i.e. an isomorphism. It follows that, as claimed:
Cubic example
If K is the rational number field Q and- p(X) = X3 − 2,
then a splitting field L will contain a primitive cube root of unity, as well as a cube root of 2. Thus
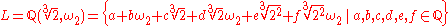
where
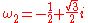, , and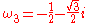are the cubic roots of unity.
Other examples
- A splitting field of
over 
is 
; the polynomial has no roots in 
, i.e., −1 is not a square there, because 7 is not equivalent to 1 (mod 4). - The splitting field of
over 
is 
since 
already factors into linear factors. - Let the base field F = Z / 2Z, the field of two elements {0, 1}, and let f(x) = x3 + x + 1. It is easy to verify that f(x) has no roots in F, hence f(x) is irreducible in F[x]. Put r = x + (f(x)) in F[x] / (f(x)) so F(r) is a field and x3 + x + 1 = (x + r)(x2 + ax + b) in F(r)[x]. Note that we can write + for - since the characteristic is two. Comparison of coefficients shows that a = r and b = 1 + r2. The elements of F(r) can be listed as c + dr + er2, where c, d, e are in F. There are eight elements: 0, 1, r, 1 + r, r2, 1 + r2, r + r2 and 1 + r + r2. Substituting these in x2 + rx + 1 + r2 we reach (r2)2 + r(r2) + 1 + r2 = r4 + r3 + 1 + r2 = 0, since r2 = r + 1 and r4 = r2 + r. Hence x2 + ax + b factors into linear factors in F(r)[x] and E = F(r) is a splitting field of x3 + x + 1 over F.