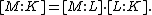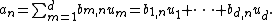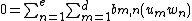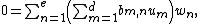Degree of a field extension
Encyclopedia
In mathematics
, more specifically field theory
, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics
, including algebra
and number theory
— indeed in any area where fields
appear prominently.
. Then E may be considered as a vector space
over F (the field of scalars). The dimension
of this vector space is called the degree of the field extension, and it is denoted by [E:F].
The degree may be finite or infinite, the field being called a finite extension or infinite extension accordingly. An extension E/F is also sometimes said to be simply finite if it is a finite extension; this should not be confused with the fields themselves being finite field
s (fields with finitely many elements).
The degree should not be confused with the transcendence degree
of a field; for example, the field Q(X) of rational function
s has infinite degree over Q, but transcendence degree only equal to 1.
In other words, the degree going from the "bottom" to the "top" field is just the product of the degrees going from the "bottom" to the "middle" and then from the "middle" to the "top". It is quite analogous to Lagrange's theorem
in group theory
, which relates the order of a group to the order and index
of a subgroup — indeed Galois theory
shows that this analogy is more than just a coincidence.
The formula holds for both finite and infinite degree extensions. In the infinite case, the product is interpreted in the sense of products of cardinal number
s. In particular, this means that if M/K is finite, then both M/L and L/K are finite.
If M/K is finite, then the formula imposes strong restrictions on the kinds of fields that can occur between M and K, via simple arithmetical considerations. For example, if the degree [M:K] is a prime number
p, then for any intermediate field L, one of two things can happen: either [M:L] = p and [L:K] = 1, in which case L is equal to K, or [M:L] = 1 and [L:K] = p, in which case L is equal to M. Therefore there are no intermediate fields (apart from M and K themselves).
{u1, ..., ud} for L over K, and a basis {w1, ..., we} for M over L. We will show that the elements umwn, for m ranging through 1, 2, ..., d and n ranging through 1, 2, ..., e, form a basis for M/K; since there are precisely de of them, this proves that the dimension of M/K is de, which is the desired result.
First we check that they span
M/K. If x is any element of M, then since the wn form a basis for M over L, we can find elements an in L such that
Then, since the um form a basis for L over K, we can find elements bm,n in K such that for each n,
Then using the distributive law and associativity
of multiplication in M we have
which shows that x is a linear combination of the umwn with coefficients from K; in other words they span M over K.
Secondly we must check that they are linearly independent
over K. So assume that
for some coefficients bm,n in K. Using distributivity and associativity again, we can group the terms as
and we see that the terms in parentheses must be zero, because they are elements of L, and the wn are linearly independent over L. That is,
for each n. Then, since the bm,n coefficients are in K, and the um are linearly independent over K, we must have that bm,n = 0 for all m and all n. This shows that the elements umwn are linearly independent over K. This concludes the proof.
A × B, which by definition has cardinality equal to the product of the cardinalities of A and B.
s E and F with F contained in E and the multiplication and addition of F being the restriction of the operations in E, we can consider E as a vector space over F in two ways: having the scalars act on the left, giving a dimension [E:F]l, and having them act on the right, giving a dimension [E:F]r. The two dimensions need not agree. Both dimensions however satisfy a multiplication formula for towers of division rings; the proof above applies to left-acting scalars without change.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, including algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
— indeed in any area where fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
appear prominently.
Definition and notation
Suppose that E/F is a field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
. Then E may be considered as a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over F (the field of scalars). The dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of this vector space is called the degree of the field extension, and it is denoted by [E:F].
The degree may be finite or infinite, the field being called a finite extension or infinite extension accordingly. An extension E/F is also sometimes said to be simply finite if it is a finite extension; this should not be confused with the fields themselves being finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s (fields with finitely many elements).
The degree should not be confused with the transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
of a field; for example, the field Q(X) of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s has infinite degree over Q, but transcendence degree only equal to 1.
The multiplicativity formula for degrees
Given three fields arranged in a tower, say K a subfield of L which is in turn a subfield of M, there is a simple relation between the degrees of the three extensions L/K, M/L and M/K:In other words, the degree going from the "bottom" to the "top" field is just the product of the degrees going from the "bottom" to the "middle" and then from the "middle" to the "top". It is quite analogous to Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, which relates the order of a group to the order and index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
of a subgroup — indeed Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
shows that this analogy is more than just a coincidence.
The formula holds for both finite and infinite degree extensions. In the infinite case, the product is interpreted in the sense of products of cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s. In particular, this means that if M/K is finite, then both M/L and L/K are finite.
If M/K is finite, then the formula imposes strong restrictions on the kinds of fields that can occur between M and K, via simple arithmetical considerations. For example, if the degree [M:K] is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, then for any intermediate field L, one of two things can happen: either [M:L] = p and [L:K] = 1, in which case L is equal to K, or [M:L] = 1 and [L:K] = p, in which case L is equal to M. Therefore there are no intermediate fields (apart from M and K themselves).
Proof of the multiplicativity formula in the finite case
Suppose that K, L and M form a tower of fields as in the degree formula above, and that both d = [L:K] and e = [M:L] are finite. This means that we may select a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
{u1, ..., ud} for L over K, and a basis {w1, ..., we} for M over L. We will show that the elements umwn, for m ranging through 1, 2, ..., d and n ranging through 1, 2, ..., e, form a basis for M/K; since there are precisely de of them, this proves that the dimension of M/K is de, which is the desired result.
First we check that they span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
M/K. If x is any element of M, then since the wn form a basis for M over L, we can find elements an in L such that
Then, since the um form a basis for L over K, we can find elements bm,n in K such that for each n,
Then using the distributive law and associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of multiplication in M we have
which shows that x is a linear combination of the umwn with coefficients from K; in other words they span M over K.
Secondly we must check that they are linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
over K. So assume that
for some coefficients bm,n in K. Using distributivity and associativity again, we can group the terms as
and we see that the terms in parentheses must be zero, because they are elements of L, and the wn are linearly independent over L. That is,
for each n. Then, since the bm,n coefficients are in K, and the um are linearly independent over K, we must have that bm,n = 0 for all m and all n. This shows that the elements umwn are linearly independent over K. This concludes the proof.
Proof of the formula in the infinite case
In this case, we start with bases uα and wβ of L/K and M/L respectively, where α is taken from an indexing set A, and β from an indexing set B. Using an entirely similar argument as the one above, we find that the products uαwβ form a basis for M/K. These are indexed by the cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
A × B, which by definition has cardinality equal to the product of the cardinalities of A and B.
Examples
- The complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s are a field extension over the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with degree [C:R] = 2, and thus there are no non-trivial fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s between them. - The field extension Q(√2, √3), obtained by adjoining √2 and √3 to the field Q of rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, has degree 4, that is, [Q(√2, √3):Q] = 4. The intermediate field Q(√2) has degree 2 over Q; we conclude from the multiplicativity formula that [Q(√2, √3):Q(√2)] = 4/2 = 2. - The finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
GF(125) = GF(53) has degree 3 over its subfield GF(5). More generally, if p is a prime and n, m are positive integers with n dividing m, then [GF(pm):GF(pn)] = m/n. - The field extension C(T)/C, where C(T) is the field of rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s over C, has infinite degree (indeed it is a purely transcendental extension). This can be seen by observing that the elements 1, T, T2, etc, are linearly independent over C. - The field extension C(T2) also has infinite degree over C. However, if we view C(T2) as a subfield of C(T), then in fact [C(T):C(T2)] = 2. More generally, if X and Y are algebraic curveAlgebraic curveIn algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s over a field K, and F : X → Y is a surjective morphism between them of degree d, then the function fieldFunction field of an algebraic varietyIn algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
s K(X) and K(Y) are both of infinite degree over K, but the degree [K(X):K(Y)] turns out to be equal to d.
Generalization
Given two division ringDivision ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s E and F with F contained in E and the multiplication and addition of F being the restriction of the operations in E, we can consider E as a vector space over F in two ways: having the scalars act on the left, giving a dimension [E:F]l, and having them act on the right, giving a dimension [E:F]r. The two dimensions need not agree. Both dimensions however satisfy a multiplication formula for towers of division rings; the proof above applies to left-acting scalars without change.