
Separable polynomial
Encyclopedia
In mathematics
, two slightly different notions of separable polynomial are used, by different authors.
According to the most common one, a polynomial
P(X) over a given field
K is separable if all its roots are distinct in an algebraic closure
of K, that is the number of its distinct roots is equal to its degree.
For the second definition, P(X) is separable if all of its irreducible factors in K[X] have distinct roots in the splitting field
of P(X), or equivalently in an algebraic closure
of K. For this definition, separability depends explicitly of the field K, as an irreducible polynomial P which is not separable becomes separable over the splitting field of K. Also, for this definition every polynomial over a perfect field
is separable, which includes in particular all fields of characteristic
0, and all finite field
s.
Both definitions coincide in case P(X) is irreducible
over K, which is the case used to define the notion of a separable extension
of K.
In the remainder of this article, only the first definition is used.
A polynomial P(X) is separable if and only if it is coprime
to its formal derivative
P′(X).
s: A field extension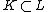 is a separable extension if and only if for every
is a separable extension if and only if for every 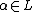 , which is algebraic over K, the minimal polynomial
, which is algebraic over K, the minimal polynomial
of over K is a separable polynomial.
over K is a separable polynomial.
Inseparable extensions (that is extensions which are not separable) may occur only in characteristic p.
The criterion above leads to the quick conclusion that if P is irreducible and not separable, then P′(X)=0.
Thus we must have
for some polynomial Q over K, where the prime number p is the characteristic.
With this clue we can construct an example:
with K the field of rational function
s in the indeterminate T over the finite field with p elements. Here one can prove directly that P(X) is irreducible, and not separable. This is actually a typical example of why inseparability matters; in geometric terms P represents the mapping on the projective line
over the finite field, taking co-ordinates to their pth power. Such mappings are fundamental to the algebraic geometry
of finite fields. Put another way, there are coverings in that setting that cannot be 'seen' by Galois theory. (See radical morphism for a higher-level discussion.)
If L is the field extension
in other words the splitting field
of P, then L/K is an example of a purely inseparable field extension. It is of degree p, but has no automorphism
fixing K, other than the identity, because T1/p is the unique root of P. This shows directly that Galois theory must here break down. A field such that there are no such extensions is called perfect. That finite fields are perfect follows a posteriori from their known structure.
One can show that the tensor product of fields
of L with itself over K for this example has nilpotent
elements that are non-zero. This is another manifestation of inseparability: that is, the tensor product operation on fields need not produce a ring that is a product of fields (so, not a commutative semisimple ring).
If P(x) is separable, and its roots form a group
(a subgroup of the field K), then P(x) is an additive polynomial
.
.
For example, let P be an irreducible polynomial with integer coefficients and p be a prime number which does not divides the leading coefficient of P. Let Q be the polynomial over the finite field
with p elements, which is obtained by reducing modulo
p the coefficients of P. Then, if Q is separable (which is the case for every p but a finite number) then the degrees of the irreducible factors of Q are the lengths of the cycles
of some permutation
of the Galois group
of P.
Another example: P being as above, a resolvent R for a group
G is a polynomial whose coefficients are polynomials in the coefficients of p, which provides some information on the Galois group
of P. More precisely, if R is separable and has a rational root then the Galois group
of P is contained in G. For example, if D is the discriminant
of P then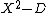 is a resolvent for the alternating group. This resolvent is always separable if P is irreducible, but most resolvents are not always separable.
is a resolvent for the alternating group. This resolvent is always separable if P is irreducible, but most resolvents are not always separable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, two slightly different notions of separable polynomial are used, by different authors.
According to the most common one, a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
P(X) over a given field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is separable if all its roots are distinct in an algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of K, that is the number of its distinct roots is equal to its degree.
For the second definition, P(X) is separable if all of its irreducible factors in K[X] have distinct roots in the splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of P(X), or equivalently in an algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of K. For this definition, separability depends explicitly of the field K, as an irreducible polynomial P which is not separable becomes separable over the splitting field of K. Also, for this definition every polynomial over a perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
is separable, which includes in particular all fields of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0, and all finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
Both definitions coincide in case P(X) is irreducible
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over K, which is the case used to define the notion of a separable extension
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
of K.
In the remainder of this article, only the first definition is used.
A polynomial P(X) is separable if and only if it is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to its formal derivative
Formal derivative
In mathematics, the formal derivative is an operation on elements of a polynomial ring or a ring of formal power series that mimics the form of the derivative from calculus. Though they appear similar, the algebraic advantage of a formal derivative is that it does not rely on the notion of a...
P′(X).
Separable field extensions
Separable polynomials are used to define separable extensionSeparable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
s: A field extension
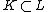 is a separable extension if and only if for every
is a separable extension if and only if for every 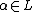 , which is algebraic over K, the minimal polynomial
, which is algebraic over K, the minimal polynomialMinimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
of
 over K is a separable polynomial.
over K is a separable polynomial.Inseparable extensions (that is extensions which are not separable) may occur only in characteristic p.
The criterion above leads to the quick conclusion that if P is irreducible and not separable, then P′(X)=0.
Thus we must have
- P(X) = Q(Xp)
for some polynomial Q over K, where the prime number p is the characteristic.
With this clue we can construct an example:
- P(X) = Xp − T
with K the field of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s in the indeterminate T over the finite field with p elements. Here one can prove directly that P(X) is irreducible, and not separable. This is actually a typical example of why inseparability matters; in geometric terms P represents the mapping on the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
over the finite field, taking co-ordinates to their pth power. Such mappings are fundamental to the algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
of finite fields. Put another way, there are coverings in that setting that cannot be 'seen' by Galois theory. (See radical morphism for a higher-level discussion.)
If L is the field extension
- K(T1/p),
in other words the splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of P, then L/K is an example of a purely inseparable field extension. It is of degree p, but has no automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
fixing K, other than the identity, because T1/p is the unique root of P. This shows directly that Galois theory must here break down. A field such that there are no such extensions is called perfect. That finite fields are perfect follows a posteriori from their known structure.
One can show that the tensor product of fields
Tensor product of fields
In abstract algebra, the theory of fields lacks a direct product: the direct product of two fields, considered as a ring is never itself a field. On the other hand it is often required to 'join' two fields K and L, either in cases where K and L are given as subfields of a larger field M, or when K...
of L with itself over K for this example has nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements that are non-zero. This is another manifestation of inseparability: that is, the tensor product operation on fields need not produce a ring that is a product of fields (so, not a commutative semisimple ring).
If P(x) is separable, and its roots form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(a subgroup of the field K), then P(x) is an additive polynomial
Additive polynomial
In mathematics, the additive polynomials are an important topic in classical algebraic number theory.-Definition:Let k be a field of characteristic p, with p a prime number. A polynomial P with coefficients in k is called an additive polynomial, or a Frobenius polynomial, ifP=P+P\,as polynomials...
.
Applications in Galois theory
Separable polynomials occur frequently in Galois theoryGalois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
.
For example, let P be an irreducible polynomial with integer coefficients and p be a prime number which does not divides the leading coefficient of P. Let Q be the polynomial over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with p elements, which is obtained by reducing modulo
Modulo
In the mathematical community, the word modulo is often used informally. Generally, to say "A is the same as B modulo C" means, more-or-less, "A and B are the same except for differences accounted for or explained by C"....
p the coefficients of P. Then, if Q is separable (which is the case for every p but a finite number) then the degrees of the irreducible factors of Q are the lengths of the cycles
Cycle (mathematics)
In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
of some permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of P.
Another example: P being as above, a resolvent R for a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a polynomial whose coefficients are polynomials in the coefficients of p, which provides some information on the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of P. More precisely, if R is separable and has a rational root then the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of P is contained in G. For example, if D is the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of P then
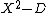 is a resolvent for the alternating group. This resolvent is always separable if P is irreducible, but most resolvents are not always separable.
is a resolvent for the alternating group. This resolvent is always separable if P is irreducible, but most resolvents are not always separable.

